自动控制原理与设计仿真练习（Gene.F.Franklin）

第二章：动态模型

1. 钟摆运动方程

问题描述：计算以下单摆运动在施加阶跃转矩$T_e$后的角度运动方程。

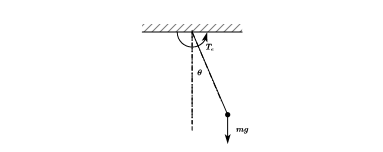
采用牛顿第二定律计算：
$$\begin{gathered} \{\begin{array}{l}\frac{T_e}{r}-mg\sin \theta \left(t\right)=\frac{dv\left(t\right)}{dt}\\ v\left(t\right)=\omega \left(t\right)r\\ \omega \left(t\right)=\frac{d\theta \left(t\right)}{dt}\end{array} \\ \text{化简可得：} \\ {T}_e-mgr\sin \theta \left(t\right)=m{r}^2\frac{d^2\theta \left(t\right)}{d{t}^2} \end{gathered}$$

直接采用刚体旋转动力学：
$T_e-mgr\sin \theta \left(t\right)=J\frac{d\omega \left(t\right)}{dt}$

两式完全等价。 因此 在一个微小的局部点，应用牛顿第二定律，等价于刚体转动方程形式。

对旋转运动进行线性化：
$$\begin{gathered} T_e\left(t\right)-mgr\theta \left(t\right)=m{r}^2\frac{d^2\theta \left(t\right)}{d{t}^2} \\ \text{左右两边进行拉普拉斯变换：} \\ {T}_e\left(s\right)-mgr\theta \left(s\right)=m{r}^2{s}^2\theta \left(s\right) \\ \frac{\theta \left(s\right)}{T_e\left(s\right)}=\frac{1}{m{r}^2{s}^2+mgr} \end{gathered}$$

分析：
原始的微分方程的零次项代表无阻尼自然震荡角频率，反映了震荡的频率。注意：极点反映的都是动态系统的衰减和震荡特性；

matlab仿真验证：

t=0:0.02:10;
num =1;
den = [1 0 9.8];
sys=tf(num,den);
y=step(sys);
subplot(2,2,1);
pzmap(sys);
grid on;
subplot(2,2,2);
bode(sys);
grid on;
subplot(2,2,3);
plot(y);
grid on;

仿真结果：

可以看到震荡频率为3.13rad/s，对应的周期为：$T_s=\frac{2\ast \pi }{\omega }$为：2s的震荡周期。与实际的时域震荡周期相符。

总结： 根平面上，根位于虚轴描述了系统的无阻尼震荡特性，而且描述系统的震荡频率（单位为rad/s），bode图上的谐振点，描述了该系统对于3.13rad/s的频率具有109db的放大效果。而对其他频率的信号没有放大效果。bode更容易通过滤波器的思维角度呈现。因此也将控制系统设计称为滤波器设计。
若增加无阻尼震荡项：

可见震荡频率增大，也就是说原始微分方程的角度1次项的系数大小描述了震荡的频率大小，当该值越大，则震荡的频率越大。

2. 延伸扩展：

线性化？

问题是如何寻找$f(x)$?

转动惯量的定义和常见物体转动惯量的计算？
对于单质量系统的转动惯量：$m{r}^2$;
对于圆盘的转动惯量：$1/2m{r}^2$

角速度vs线速度？
$v=\omega r$

第三章：动态响应

注意：在做零极点分布分析时，是对输出的拉普拉斯变换进行分析。因为输入不同，输出信号的拉普拉斯变换也不同。

计算终值：

计算式：$y\left(s\right)=\frac{3\left(s+2\right)}{s\left(s^2+2s+10\right)}$所对应的系统的终值：
$y\left(\propto \right)=sY\left(s\right){\mid }_{s=0}^{}=0.6$

注意计算终值时，用的输出的拉普拉斯变换表达式。而不是传递函数。
终值定理也可以用来计算直流增益：
即对于阶跃输入的系统的稳态终值：
$\underset{s\to 0}{\lim }sG\left(s\right)\frac{1}{s}$
即传递函数在$s=0$时，表示传递函数的直流增益。

扩展延伸

常见信号的拉普拉斯变换：
$$\begin{gathered} \sigma \left(t\right)\stackrel{\mathcal{L}}{\to }1 \\ 1\left(t\right)\stackrel{\mathcal{L}}{\to }\frac{1}{s} \\ t\stackrel{\mathcal{L}}{\to }\frac{1}{s^2} \\ {t}^2\stackrel{\mathcal{L}}{\to }\frac{2!}{s^3} \\ {e}^{-at}\stackrel{\mathcal{L}}{\to }\frac{1}{s+a} \\ \sin at\stackrel{\mathcal{L}}{\to }\frac{a}{s^2+a^2} \\ \cos at\stackrel{\mathcal{L}}{\to }\frac{s}{s^2+a^2} \\ {e}^{-at}\cos bt\stackrel{\mathcal{L}}{\to }\frac{s+a}{{\left(s+a\right)}^2+b^2} \\ {e}^{-at}\sin bt\stackrel{\mathcal{L}}{\to }\frac{b}{{\left(s+a\right)}^2+b^2} \end{gathered}$$
例子：绘制以下传递函数的响应：$H\left(s\right)=\frac{100s}{s^3+10.1s^2+101s}$

由传递函数可知该信号在原点处有一个极点，表明该信号具有稳态分量，稳态值为：
$\underset{s\to 0}{\lim }sY\left(s\right)=s\frac{100}{s^2+10.1s^2+101s}{\mid }_{s=0}^{}=\frac{100}{101}=0.990099$

另外复极点实部为$-5.05$，意味着衰减速度为：$e^{-5.05t}$，即当$t=1/5.05$时，震荡分量的幅值衰减至原始幅值的0.36倍。另外由于复极点的虚部为：$8.69rad/s$，即震荡周期为：$2\pi /w=0.72s$与时域响应基本吻合。

根据方框图计算闭环传递函数？
$H\left(s\right)=\frac{G_1\left(s\right)}{1+G_1\left(s\right)G_2\left(s\right)}$，其中G1为前向通道传递函数，G2为反馈回路的传递函数。
绘制如下传递函数系统的脉冲响应：$H\left(s\right)=\frac{2s+1}{s^2+2s+5}$

num=[2 1];
den = [1 2 5];
sys =tf(num,den);
t=0:0.01:6;
y=impulse(sys,t);
plot(t,y);
grid on

运行结果：

$H\left(s\right)=\frac{2s+1}{s^2+2s+5}=\frac{2s+1}{{\left(s+1\right)}^2+2^2}$
表示了上述系统的极点为复极点，实部为-1，虚部为$-2$。即振荡周期为：$\pi$。

劳斯判据

例：利用劳斯判据计算如下特征方程的稳定区间：
$\begin{array}{ccc}1& k-6& \\ 5& k& \\ \frac{4k-30}{5}& 0& \\ k& & \end{array}$
因此可根据：$4K-30>0;k>0$获得稳定区间：$k>7.5$
采用pzmap分别绘制在k=4，7.5，10时的根分布情况。

clc;clear;
s=tf('s');n=1;
for k=5:2.5:10
g1=k*(s+1)/(s*(s-1)*(s+6));
g2=1;
G12=feedback(g1,g2);
subplot(1,3,n);
pzmap(G12);
n=n+1;
hold on 
grid on
end

当k为5，7.5,10时的根分布和阶跃响应如下图所示：

采用实验数据拟合处传递函数中，关于对数函数的性质特此复习总结：
$$\begin{gathered} {\log }_a\left(NM\right)={\log }_{a}N+{\log }_{a}M \\ {\log }_a\frac{N}{M}={\log }_{a}N-{\log }_{a}M \\ {\log }_a{N}^m=m{\log }_{a}N \\ \text{证明：由于对数是指数的逆运算；} \\ \text{假设：}{a}^x=N\text{，}{a}^y=M \\ \text{则：}{a}^{x+y}=a^x{a}^y=NM,\text{即：}x+y={\log }_{a}NM,\text{而}x={\log }_{a}N,y={\log }_{a}M \\ \text{故：}{\log }_{a}N+{\log }_{a}M={\log }_{a}NM \end{gathered}$$

反馈系统的基本概念

$$\begin{gathered} \text{对于开环传递函数}G\left(s\right)D\left(s\right)=\frac{b\left(s\right)c\left(s\right)}{a\left(s\right)d\left(s\right)}\text{，若只是开环控制在，则稳定的条件是}ad\text{没有}RHP \\ \text{若采用闭环负反馈控制则特征根为：} \\ 1+G\left(s\right)D\left(s\right)=0\text{，即}b\left(s\right)c\left(s\right)+a\left(s\right)d\left(s\right)=0\text{，因此原始开环传递的负极点不影响我们设计一个使系统稳定的控制器。} \end{gathered}$$

这也是闭环负反馈的优势所在。
灵敏度定义：控制对象的增益偏差变化量引起的闭环传递函数增益变化量的比值；
$S_G^{T_{cl}}=\frac{\delta T_{cl}/T_{cl}}{\delta G/G}=\frac{G}{T_{cl}}\frac{\delta T_{cl}}{\delta G}$
化简结果如下式所示： $S_G^{T_{cl}}=\frac{G}{\frac{GD}{1+GD}}\frac{\left(1+GD\right)D-D\left(GD\right)}{{\left(1+GD\right)}^2}=\frac{1}{1+GD}$
不同系统型别对不同输入的误差响应：位置误差、速度误差、加速度误差的计算原理是：终值定理。
以输入的不同误差计算为例：

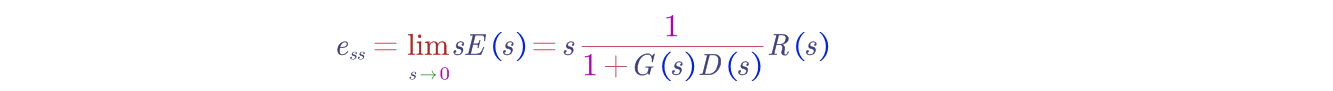
例：计算对下述传递函数的离散化差分方程：
$$\begin{gathered} D\left(s\right)=1.4\frac{s+6}{s} \\ \text{将}s=\frac{2}{T_s}\frac{z-1}{z+1}\text{带入控制方程：} \\ D\left(z\right)=1.4\frac{\frac{2}{T_s}\frac{z-1}{z+1}+6}{\frac{2}{T_s}\frac{z-1}{z+1}}=\frac{1.4\left(z-1\right)+1.4\ast 3T_s\left(z+1\right)}{\left(z-1\right)}=\frac{1.4z+4.2T_{s}z-1.4+4.2T_s}{z-1} \\ \text{当}{T}_s=0.07\text{时：}1.4+4.2\ast 0.07=1.694 \\ D\left(z\right)=\frac{1.694z-1.106}{z-1} \end{gathered}$$
采用matlab计算：

s=tf('s');
g1=1.4*(s+6)/s;
z1=c2d(g1,0.07,'t');

计算结果：

查漏补缺：matlab进行离散化的不同方式：

SYSD = c2d(SYSC,TS,METHOD) computes a discrete-time model SYSD with sample time TS that approximates the continuous-time model SYSC.
The string METHOD selects the discretization method among the following:
‘zoh’ Zero-order hold on the inputs
‘foh’ Linear interpolation of inputs
‘impulse’ Impulse-invariant discretization
‘tustin’ Bilinear (Tustin) approximation.
‘matched’ Matched pole-zero method (for SISO systems only).
The default is ‘zoh’ when METHOD is omitted. The sample time TS should
be specified in the time units of SYSC (see “TimeUnit” property).

根轨迹设计法

控制系统的根轨迹形式：
$\begin{array}{c}1+k\frac{a\left(s\right)}{b\left(s\right)}=0\\ b\left(s\right)+ka\left(s\right)=0\\ 1+kL\left(s\right)=0\end{array}$
由于k变化时，s的值即为闭环系统的根，也是系统的闭环极点，因此根轨迹也可作为通过控制k的变换从而调节闭环系统的动态性能。

根轨迹的定义：
定义一：当k从0变化为正无穷大时，闭环特征方程：$1+KL(s)=0$的s所满足的集合。
定义二：根据相角条件，由于s为复数，因此原始的特征方程满足：$L(s)=-1/k$，根据相角条件可知L(s)即开环传递函数的零极点与测试s点满足以下相角条件。
$\sum \left(s-{\psi }_z\right)-\sum \left(s-{\psi }_p\right)=180+n\ast 360$
其中${\psi }_z$为开环传递函数的零点，${\psi }_p$为传递函数的极点。
Dr.Can says:根据根轨迹的定义可以通过相角条件实现零极点匹配。

一般根轨迹由于相角条件为180度，因此也称180度根轨迹。
主要规则：

1. n条分支从极点出发到零点和无穷远。
2. 实轴上根轨迹位于奇数个零极点的左侧；（注意只是实轴上）
3. n-m条根轨迹趋向于无穷远。而且倾斜角为$180+a\ast 360/(n-m)$

s=tf('s');
g1=1/(((s+2)^2+2)*((s+1)^2+5));
rlocus(g1);

例：绘制以下图像的根轨迹：$L\left(s\right)=\frac{1}{s\left(s^2+8s+32\right)}$

s=tf('s');
g1=1/(s*(s^2+8*s+32));
rlocus(g1);

根据原始传递函数可知：开环传递函数存在三个极点，分别为原点的极点和i两个共轭复极点。表明该系统为1型系统，可以实现阶跃信号的无差跟踪。三个极点表明系统根轨迹有3条指向无穷远，渐近线为60度，180度，300度。因此有两条根轨迹将穿过虚轴，因此存在临界增益K。如何计算增益k值？可以根据幅值条件计算。
$$\begin{gathered} 由于k=-\frac{1}{L\left(s\right)} \\ \text{因此根轨迹上的点必然满足上式。以下面的开环传递函数为例：} \\ L\left(s\right)=\frac{1}{s\left(s+a\right)\left(s+b\right)} \\ \text{则若根轨迹过}{s}_0\text{点则：} \\ k=\left|s_0\right|\left|s_0+a\right|\left|s_0+b\right| \end{gathered}$$

超前补偿的含义：相对于输入的正弦信号，输出的信号相位与输入信号相比具有超前作用。

频率响应分析法

注意当系统的输出存在正弦响应时，可能是系统的输入存在正弦响应，原因是：$G(s)R(s)$的拉普拉斯反变换中存在输入信号的拉普拉斯反变换。
$Y\left(s\right)=G\left(s\right)\frac{Aw}{s^2+w^2}$

在进行频率响应分析时，最终输出的幅值和相位变化是有闭环传递函数的幅相频特性决定的。
采用matlab仿真简单的超前补偿器的bode图：$D\left(s\right)=k\frac{s+1}{0.1s+1}$

num=[1 1];
den=[0.1 1];
sys=tf(num,den);
bode(sys);
grid on;

由上图可以看到 $零点为w=1，极点为w=10$,对于零点而言，当角频率越大幅值增益越大，因此通过零点后幅值增益提高，而极点由于在分母，因此通过极点后幅值减小。另外相频方面，零点在分子因此相位超前90度，而通过极点后相位滞后90度。由于极点的角频率大于零点角频率，因此高频增益大于低频增益，高频相位超前低频相位，因此将该矫正器称为超前补偿器。

带宽的定义：系统输出能令人满意地跟踪输入正弦波的最大频率。带宽是衡量响应速度的指标。

bode图的特征：采用对数尺度绘制幅频曲线，用线性尺度绘制相频曲线。bode图法的理论依据：
$G\left(j\omega \right)=\frac{r_1{e}^{j{\theta }_1}{r}_2{e}^{j{\theta }_2}}{r_4{e}^{j{\theta }_4}{r}_5{e}^{j{\theta }_5}{r}_6{e}^{j{\theta }_6}}=\frac{r_1{r}_2}{r_4{r}_5{r}_6}{e}^{j\left({\theta }_1+{\theta }_2-{\theta }_4-{\theta }_5-{\theta }_6\right)}$

对幅值项取对数：
$\lg \left|G\left(j\omega \right)\right|=\lg r_1+\lg r_2-\lg r_4-\lg r_5-\lg r_6$
上式表明各个项的对数相加即可得到复合表达式的幅值的对数。

什么是分贝？

以分贝为单位的幅相频表示写法：
$$\begin{gathered} G\left(j\omega \right)=K_0\frac{j\omega {\tau }_1+1}{{\left(j\omega \right)}^2\left(j\omega {\tau }_a+1\right)} \\ \angle G\left(j\omega \right)=\angle K_0+\angle \left(j\omega {\tau }_1+1\right)-2\angle \left(j\omega \right)-\angle \left(j\omega {\tau }_a+1\right) \\ {\left|G\left(j\omega \right)\right|}_{dB}=20\lg \left|K_0\right|+20\lg \left|j\omega {\tau }_1+1\right|-40\lg \left|j\omega \right|-20\lg \left|j\omega {\tau }_a+1\right| \end{gathered}$$

实践演练

例6.3：绘制以下传递函数的伯德图：$G\left(j\omega \right)=\frac{2000\left(s+0.5\right)}{s\left(s+10\right)\left(s+50\right)}$
首先采用matlab绘制：

s=tf('s');
G=2000*(s+0.5)/(s*(s+10)*(s+50));
bode(G);
grid on;

分析：原始传递函数先化简为：$G\left(j\omega \right)=\frac{2\left(\frac{j\omega }{0.5}+1\right)}{j\omega \left(\frac{j\omega }{10}+1\right)\left(\frac{j\omega }{50}+1\right)}$零点转折点w=-0.5，极点转折点w=0,w=10,w=50$.在初始阶段：幅频曲线由$\frac{2}{j\omega}$决定，即幅值关系为：$20\lg |\frac{2}{j\omega }|=20\lg 2-20\lg \omega$，随后遇到零点为$0.5rad/s$后斜率发生转折，由$-20dB/dec变化为0dB/dec$，在遇到$10rad/s和50rad/s$后转折变化为$-20dB/dec和-40dB/dec$。

例：6.4绘制下图的bode图：$G\left(s\right)=\frac{10}{s\left[s^2+0.4s+4\right]}$
采用matlab绘制伯德图：

s=tf('s');
G=10/(s*(s^2+0.4*s+4));
bode(G);
grid on;

绘制结果如下图：

注意图中涉及复极点的伯德图绘制，对于二阶复极点，在自然震荡角频率处，幅频曲线的峰值为：$20\lg \left|G\left(j\omega \right)\right|=20\lg \frac{1}{2\xi }=20\lg \frac{1}{0.2}=13.9794$，本例中，阻尼系数为0.1，因此二阶复极点贡献的谐振点的峰值约为：14dB.

开环传函判定闭环传递函数稳定的理论依据是什么？

生词

pulley : 滑轮；

下一步计划

于2022年底前完成状态空间法的复习和数字控制器设计的复习。