HDOJ-1542 Atlantis 扫描线

扫描线算法的核心思想在于使用线段树对扫描线线段的长度进行维护。因此，如果平行于x轴做扫描线，那么就需要以所有的端点的x坐标为端点，以这些端点组成的线段为线段树叶子节点存储的对象，从而对扫描线的长度进行维护。

另外，说明下代码中cnt的作用。这个标记代表看似是一个lazy tag，但又不是，因为这个标记是不会往子节点传的（及不能使用pushdown操作）。扫描线算法中，叶子节点（代表的是每一个小段）和非叶子节点（代表几个小段的拼接）的cnt值是独立的，代表的按照线段树的分法，恰好被完全覆盖的次数（前提是父节点没有被完全覆盖）。因此，如果当前节点的cnt值为0了，至要它还有子节点，它的sum依然可以由子节点求和得到（虽然整段覆盖的没有了，但还可能在这个区间中有部分的覆盖存在）。

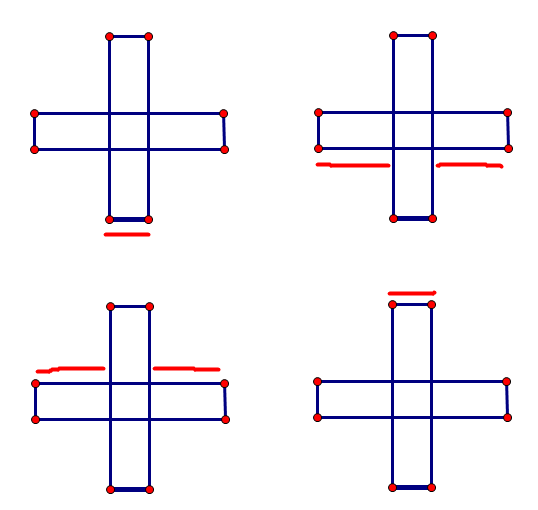
下图为cnt的作用。图了颜色代表cnt加了1.

#include <bits/stdc++.h>using namespace std;
using ll = long long;
const int INF = 2e9;
const int MAXN = 2e5+5;struct line {double x1, x2, y;int flag;line(){}line(double x1, double x2, double y, int flag){this->x1 = x1, this->x2 = x2, this->y = y; this->flag = flag;}friend bool operator < (const line &a, const  line &b){return a.y < b.y;} 
};vector<double> sum(MAXN << 3, 0);
vector<int> cnt(MAXN << 3, 0);line lines[MAXN <<1];
double P[MAXN<<1];void pushUp(int id, int l, int r){if(cnt[id]){ sum[id] = P[r] - P[l - 1];}//后面都是cnt为0的情况，cnt为1代表区域中所有的边都被选中else if(r == l) sum[id] = 0;  //只有一段，那么就直接这一段为0else {       //有多段，那么这多段为后续节点的求和sum[id] = sum[id << 1] + sum[id << 1|1];}
}void update(int id, int l, int r, int L, int R, int flag){if(L <=l && r <= R){cnt[id] += flag;pushUp(id, l, r);return;}int mid = (l + r) >> 1;if(L <= mid){update(id << 1, l, mid, L, R, flag);}if(R > mid){update(id << 1|1, mid+1, r, L, R, flag);}pushUp(id, l, r);return;
}signed main(){int n; double x1, y1, x2, y2;int ca = 1;while(true){double ans=0;for(int i = 0; i < sum.size(); i++){sum[i]=0; cnt[i]=0;}scanf("%d", &n); if(n==0) break;for(int i = 0; i < n; i++){scanf("%lf %lf %lf %lf",&x1, &y1, &x2, &y2);lines[i*2] = line(x1, x2, y1, 1);lines[i*2+1] = line(x1, x2, y2, -1);             P[i*2] = x1;P[i*2+1] = x2;}sort(lines, lines+2*n);sort(P, P+2*n);int d = unique(P, P+2*n) - P; //实际不重合的端点数目for(int i = 0; i < n * 2 -1; i ++){int l = lower_bound(P, P+d, lines[i].x1) - P + 1;int r = lower_bound(P, P+d, lines[i].x2) - P + 1;update(1, 1, d-1, l, r-1, lines[i].flag);ans += sum[1] * (lines[i+1].y - lines[i].y);}printf("Test case #%d\nTotal explored area: %.2lf\n\n", ca++, ans);}return 0;
}