OOD : DMAD Diversity-Measurable Anomaly Detection

本文主要是介绍OOD : DMAD Diversity-Measurable Anomaly Detection，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Diversity-Measurable Anomaly Detection

基于重建的异常检测模型通过抑制异常的泛化能力来迭代学习。然而，由于这种抑制，不同的正常模式的重建效果也会变得不理想。为了解决这个问题，本文提出了一种称为多样性可测量异常检测（DMAD）框架，旨在能够增强重建多样性的同时拥有抑制异常泛化的能力。作者评估了模型在视频监控和工业缺陷检测场景中的效果。为了在后一种情况下应用DMAD，作者提出了PDM的变体PPDM，以处理纹理重建中的误报问题。大量的实验结果验证了该方法的有效性。此外，提出的方法即使在受污染的数据和类似异常的正常样本检测面前也表现良好。本文工作的主要贡献如下：

引入了多样性可测量的异常检测框架，该框架允许基于重建的模型在重建不同正常样本和检测未知异常样本之间实现更好的权衡。
提出了金字塔变形模块PDM来实现多样性测量，其中变形信息与紧类原型明确分离，并且得到的多样性测量与异常呈正相关。
方法优于以前在视频异常检测和工业缺陷检测方面的工作，并且在受污染的数据和类似异常的正常样本数据上的效果很好，证明了其广泛的适用性和鲁棒性。

例子

基于重建的异常检测方法的性能长期以来一直受到一个棘手问题的制约，即重建多种模式的正常样本和检测未知异常样本之间的权衡(重建时需要确保正常模式的结果足够好，异常模式的结果足够差)。为了更容易区分异常，前人在自编码过程中施加了更多的约束来抑制异常信息，但是这导致了不同正常实例的高重构误差。例如，在图1和图2中，严重变形的正常（异常样本）样品“7”的误差甚至高于异常样品“4”。

在这里插入图片描述

图 1.MNIST数据集中异常检测难度的说明。原型用橙色三角形表示，异常用红点表示。在这种情况下，在高维特征空间中，基于重构误差或距离，很难检测到异常。我们的解决方案如图 2 所示。

在这里插入图片描述

图2. 白色数字是异常分数。a) 输入;b）重构; c）粗变形; d）微变形; e）多样性的衡量; f）变形增强分数 g）像素级重建误差分数。变形增强为异常样本分配的异常分数低于真实异常;像素级重建误差会产生不正确的异常分数。

解决方案

解决上述权衡问题的关键是找到正常和异常样本所具有的多样性的适当度量，这与异常的严重程度呈正相关。请注意，像素级重建误差并不是多样性的理想测量方法，因为高误差区域经常将异常与不同的正常特征混淆，例如，具有结构变形的正常样本和颜色接近背景的异常可能会产生不可靠的重建误差。
DMAD框架，用于增强重建多样性的可测量性，从而更准确地测量异常。我们的基本思想是将重建解耦为正常原型的紧凑表示和更多样化正常和异常的可测量变形。（Our basic idea is to decouple the reconstruction into compact representation of prototypical normals and measurable deformations of more diverse normals and anomalies.）被低估的重建误差可以通过多样性来补偿，多样性可以被适当测量。为此，DMAD框架包括一个金字塔形变模块（PDM）来建模和测量多样性，以及一个信息压缩模块（ICM）来学习原型法态模式。
假设：受[4,15]的启发，我们假设异常（例如在视频监控中）可以表示为外观的显着变形，包括位置变化和精细运动。相比之下，不同的正常样品可以表示为较弱的变形，因此很容易区分。
PDM:我们设计了 PDM 来模拟正常样本的多样性以及异常的严重程度。更具体地说，PDM 学习分层二维变形场（图 2c，d），这些场描述了像素级变换方向和从参考（图 2b，从内存中的原型重建）到原始输入的距离。
ICM:在ICM中，我们将压缩表示学习为稀疏原型。因此，单个内存项足以表示每个正常的集群。这比其他需要多个内存项的基于内存的作品更紧凑。通过将PDM与ICM集成，DMAD基本上将变形信息（图2e）与类原型解耦，并使最终的异常分数更具判别力（图2f）。

3. 多样性可测量异常检测

在本节中，我们首先分析了基于重建的异常检测的目标，并提出了一个多样性可测量的框架来解决现有工作中的权衡问题。然后，引入信息压缩模块和金字塔变形模块（PDM）作为框架的实现。最后，我们解释了训练和推理过程，以及如何将该框架应用于PDM变体的缺陷检测。

3.1. 框架

给定输入 x，基于重建的自编码器的方法旨在通过最小化以下重建损失来学习正常样本数据分布：
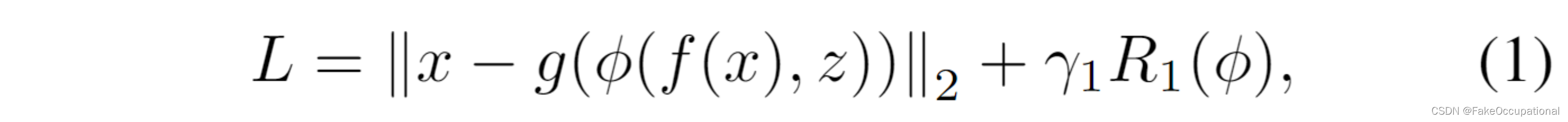
在这里插入图片描述
关于编码器f(·)、解码器g(·)、潜在变量z（存储器项）和(对应于其约束R()的)约束特征映射函数φ(·)。引入跳过连接和concate [·， ·] 来生成多样化的正常模式 [29MNAD方法]：

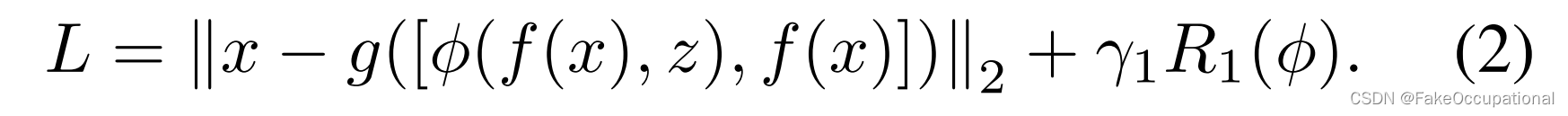
然而，由于数据分布的多样性，以往的方法不得不面对表示多样性正常和检测异常之间的冲突。其内在原因在于多样性的编码[·， f （x）]包含无法准确测量的冗余信息。

在这项工作中，我们提出了一个原则性框架，Diversity-Measurable Anomaly Detection (DMAD)，以缓解冲突。基本思想是限制向解码器g(·)传输异常信息，同时测量和模拟剩余部分的多样性。为此，我们在DMAD框架下设计了信息压缩模块φ（·）和多样性感知模块ψ（·）：

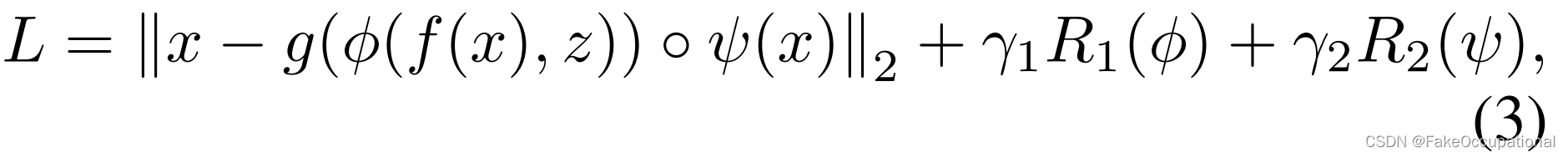
在这里插入图片描述
其中 ◦ 是指聚合运算符。通过对φ(·)、ψ(·)和约束条件进行适当的设计，优化重构损失可以提高特征嵌入的紧凑性。因此，通过φ（·）将不同的表示映射到内存中的紧凑原型。输入 x 相对于其重构的多样性用 ψ(·) 表示。被低估的重建误差可以通过以ψ（·）为单位测量的多样性来补偿，这是有助于准确异常分数的关键因素。

该框架可以在满足以下条件（图3）的前提下实现我们的目标：1. $φ$ (·)可以学习从原型模式到任何正常输入的所有不同信息，以确保正常样本不会产生高异常分数;2. $ψ$ (·)产生的变形与多样性测度呈正相关;3. $ψ$ (·)表示的x原型信息需要最小化。在以下小节中，我们将解释如何设计模块来满足这些条件。

在这里插入图片描述

pipeline

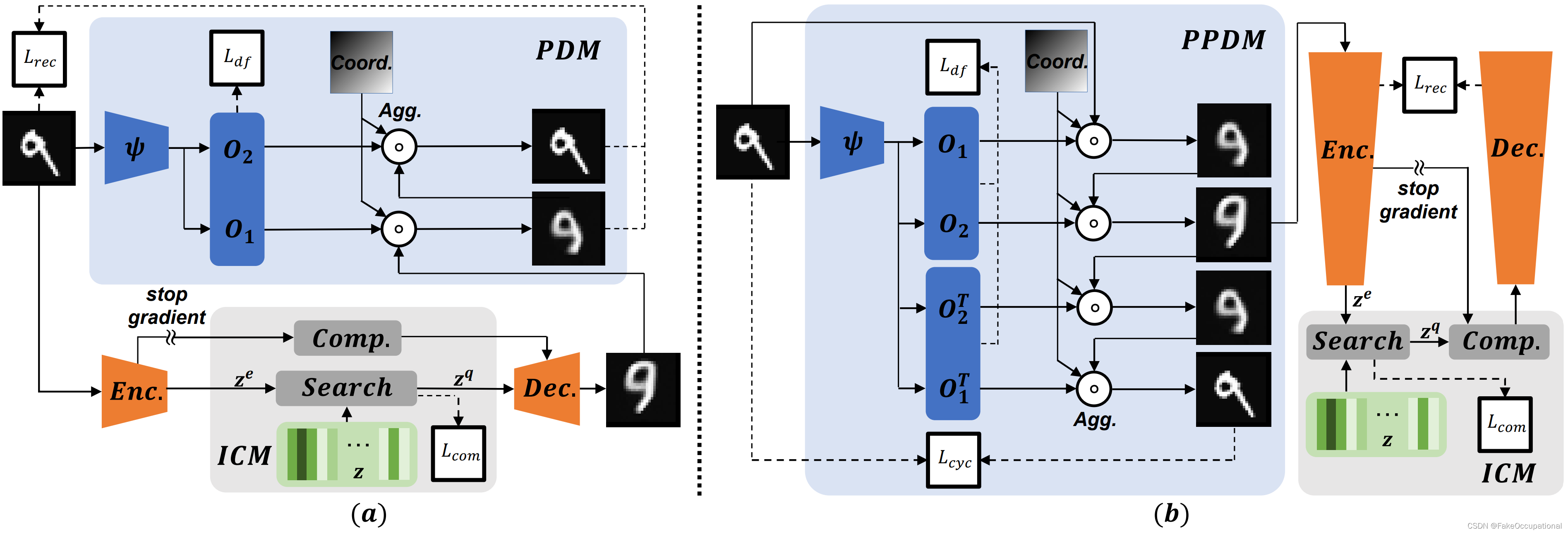
在这里插入图片描述

图4.两个版本的多样性可测量异常检测框架。多尺度金字塔形变场估计为O，逆过程估计为 $O^T$ 。a）PDM版本计算重建后的正向变形O。b） PPDM版本采用循环一致的前向-后向变形，并将前向变形施加在输入上。

3.2. 信息压缩模块 ICM

之前的重构方案每个查询向量与内存中的多个原型有联系，他们共同贡献查询结果，即使异常投影离原型很远。因此，在原型嵌入之间的低似然区域中分布的异常很难从不同的正常（记忆特征）中识别出来。根据 [35]，我们将 VQ-Layer 改编为信息压缩模块，在给定嵌入 $R^{D\times H' \times W'}$ 作为查询项 $z^e= f(x)$ 和内存特征空间 $∈R^{D\times N}$ 的情况下学习 φ（·）。然后，我们通过寻找具有最小 L2 距离的内存项（图 4 中的“搜索”）的方式将 $z^e$ 量化为单个内存特征 $z^q∈ R^{D\times H' \times W'}$ ：
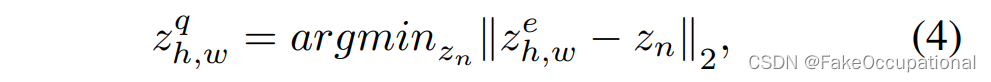
在这里插入图片描述

其中 $z_n$ 是第n个memory 项， $h ∈ \{1， · · · ， H\} ， w ∈ \{1， · · · ， W'\}$ 表示 $z^q$ 和 $z^e$ 中的相同位置。使用stop-gradient operator SG（·）单独更新其参数的压缩损失 $L_{com}$ [35]由超参数β组合：

在这里插入图片描述

低信息容量的跳跃连接（图4 “Comp.”）也允许在不带来过度泛化的情况下进一步提高重建质量（即，对于折减系数为16或更大的中间特征，使用带有停止梯度算子的Conv-Layer）。

3.3. 金字塔变形模块 PDM

我们将未知异常分为以下三种类型：未见的异常（如新物体）、全局异常（如意外运动）和可见类别的局部异常（如奇怪的行为和工件损坏）。根据重构结果，未见过的异常类很容易被检测出来，但后两种类型通常与不同的正态相混淆。为了将这些异常与正常异常区分开来，我们使用重建参考和原始输入之间的可测量变形来表示多样性，正常样本中发生轻微变形，而异常中发生剧烈变形。

受STN和DCN[4,15]的启发，我们引入了金字塔变形模块（PDM），该模块显式学习具有分层尺度的变形场，以模拟不同异常类型的运动、行为和缺陷，如图4a所示。具体来说，在特征提取后，ψ（·）使用K个头来计算偏移量 $O= \{O_1， · · · ， O_K\}$ ，图4中K=2，对应于K粗到细变形：
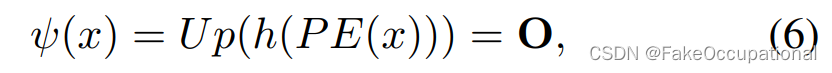
在这里插入图片描述

其中 $PE (\cdot)$ 是位置嵌入算子 [18]， $R^{C\times H\times W}→R^ { 2\times \{ H_1\times W_1,…，H_K\times W_K \} }$ 是生成偏移矢量的变形估计器， $U p (\cdot)$ 是上采样函数，用于将 K 头的输出大小调整为与原始图像相同的大小。在我们的实验中，我们设置 K = 2，其中 $O_1$ 用于估计粗变形（例如，对应于行人的位置或工件的位置）， $O_2$ 用于估计细小变形（例如，对应于行人行为或工件细节）。

考虑到没有位置信息的量化嵌入可能导致重建不准确，我们还为解码器g（·）引入了位置嵌入算子。然后，我们将 O 聚合到重建的参考 $g(PE(z^q))$ 上，并得到 $\tilde x_k(k = 1， . . . ， K)$ ，它是变形场的k层校准的结果：

$\tilde x_k =g(PE(z^q)) \circ O_1 \cdot \cdot \cdot O_k \tag{7}$

其中 ◦ 是在此实现中具有参考坐标的网格采样函数（图 4 中的“Agg.”和“Coord.”）。然而，最小化相对于ψ（x）的无约束重建损耗可能会导致编码器f（·）的退化解。为了解决这个问题，我们使用梯度操作的平滑度损失和强度损失来添加约束，如下所示：
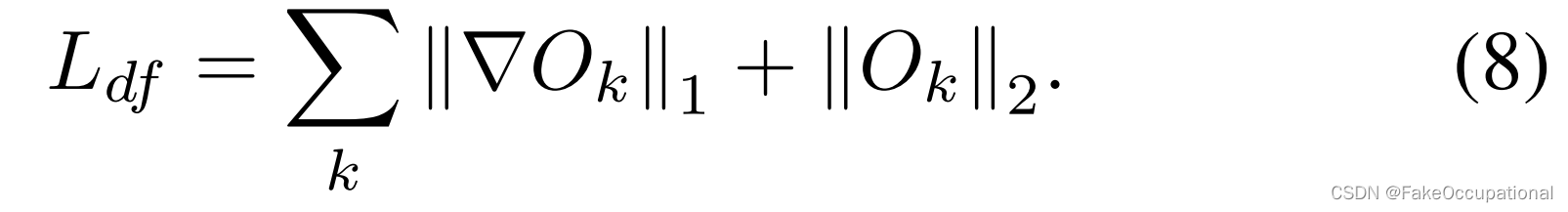
在这里插入图片描述

3.4. 前景-背景选择

将背景信息存储在内存中会破坏嵌入的紧凑性，并且需要大量的内存项。此外，变形估计不应应用于背景。有些方法使用外部估计器来消除背景干扰，但无法保证不同场景下的泛化，不可避免地会引入额外的噪声。得益于固定视场视频的强先验，我们使用可学习的模板 x 对背景进行建模，并使用 f（·）生成二进制掩码来指示像素是属于前景还是背景。最后的重建为：

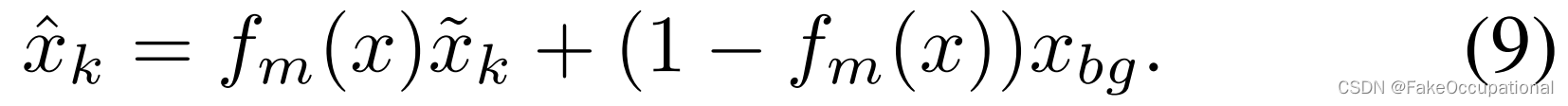
在这里插入图片描述

3.5. 训练和推理

训练阶段。

一旦我们得到重建 $\hat x$ ，我们可以计算重建损失：

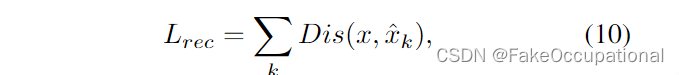
在这里插入图片描述

其中 Dis（·）是指样本空间中的距离函数。提醒式 3 中的优化目标，我们分别使用 $L_{com}$ 和 $L_{df}$ 实现这两个约束。
最后，通过最小化总体损失来执行训练：
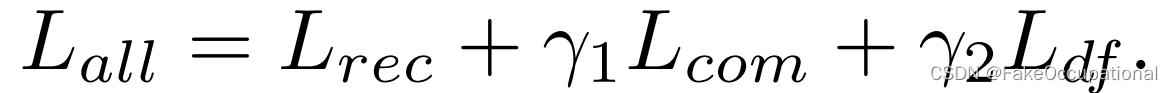
在这里插入图片描述

推理阶段

在推理阶段，我们使用 O 和重构损失来计算输入样本 x 的误差映射：

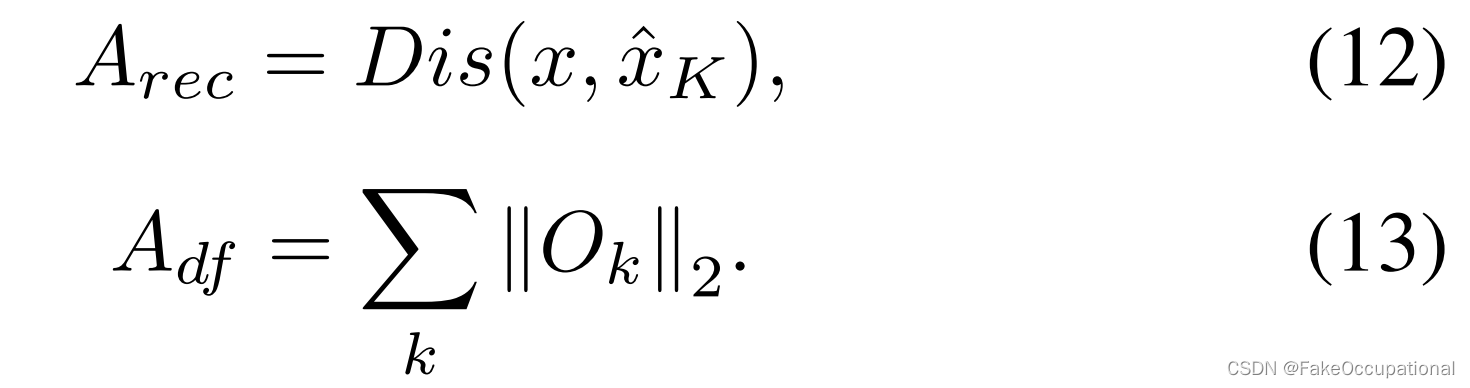
在这里插入图片描述

图像级异常分数是根据局部最大值计算的：

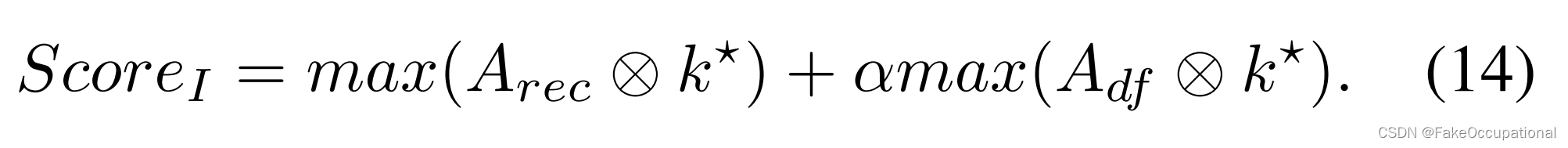
在这里插入图片描述
其中 ⊗ 是卷积算子，KIS 卷积核用于异常映射。α是一个权衡参数。也就是说，重建损失和变形共同决定了异常评分，这比传统的基于重建的方法要有效得多，如图3所示。

3.6. Variant of PDM

3.6. 带有 Pre-PDM 的 PDM 修改框架的变体。

DMAD框架以及上面提出的ICM和PDM模块适用于许多异常检测场景，包括视频监控。然而，对于工业缺陷检测，纹理重构可能是有害的（例如“Pill”上的斑点），我们应该重构高级语义特征。由于 PDM 在高维特征空间中不起作用并且会干扰训练过程，因此我们提出了 PDM 的变体 Pre-PDM （PPDM）作为解决方案。PPDM在样本空间中工作，并应用于输入样本而不是重建样本。式（3）自然修改如下：

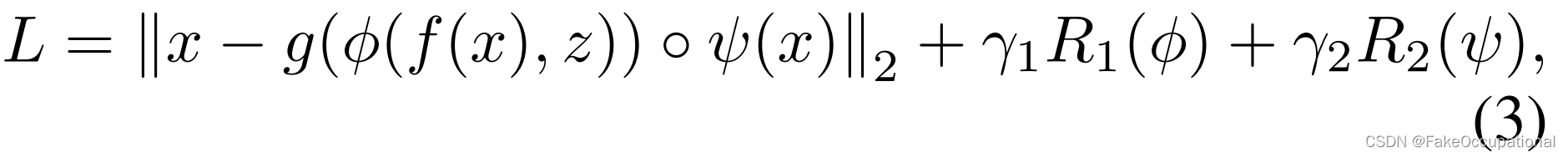
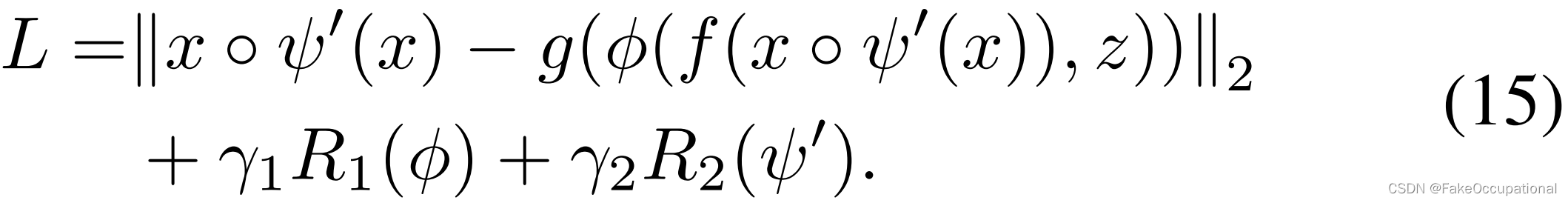
在这里插入图片描述

在这里插入图片描述
由于我们没有对原始样本进行重构，因此重构损失不能约束PPDM保持信息多样性。为了防止式（15）中的 $x ◦ ψ^{'} (x)$ 进行捷径学习，我们提出基于循环一致性原理，增加前向变形、后向变形 $O^T$ ，以保持外观信息的多样性：

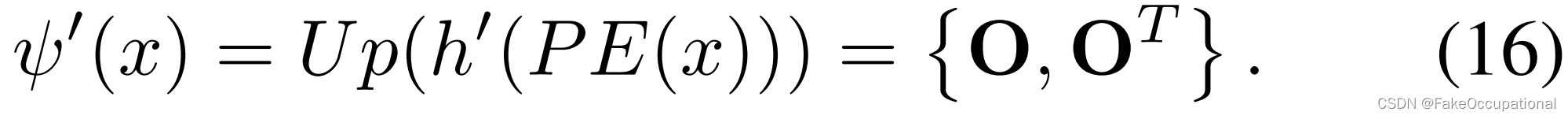
在这里插入图片描述

训练阶段。前向-后向变形损失 $L_{df}^+$ 和循环一致性损失约束 $L_{cyc}$ ：

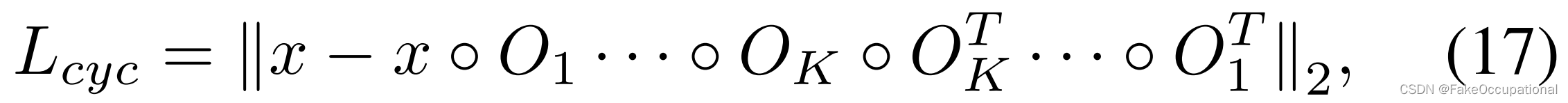
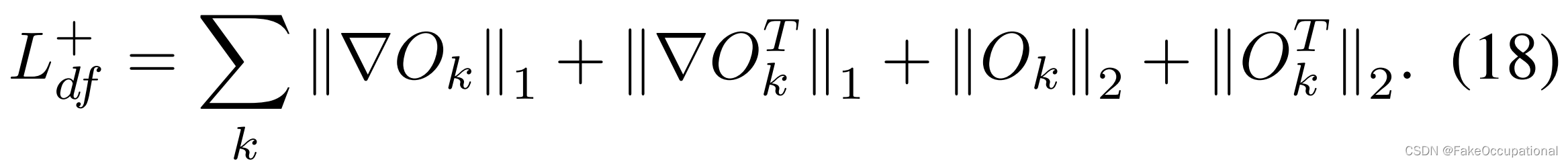
在这里插入图片描述

因此，通过最小化以下损失来使用 PPDM 训练异常检测模型：

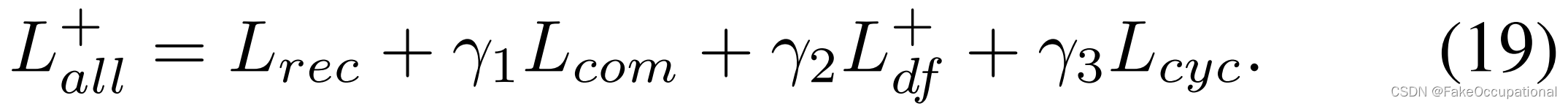
在这里插入图片描述

推理阶段 PPDM 的结果与原始输入的位置不一致，这可能会降低异常定位的性能。为了获得真实位置的异常图，我们使用反向变形进行逆采样（图5）：
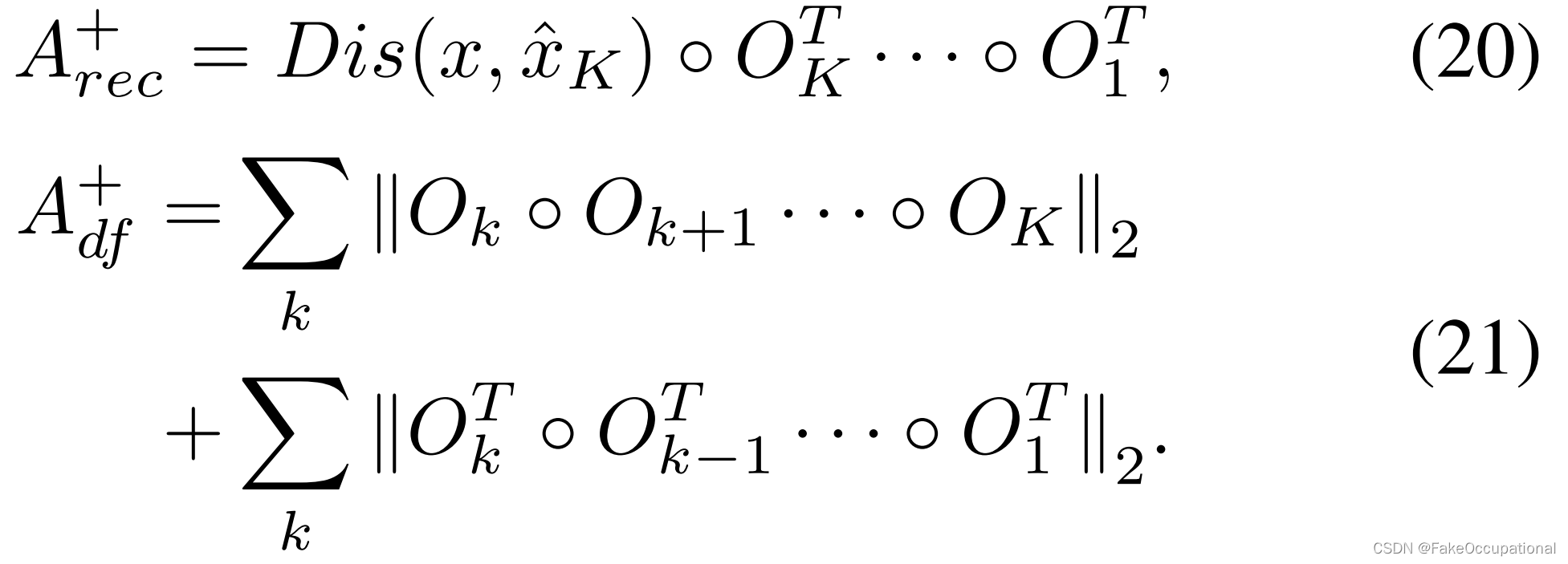
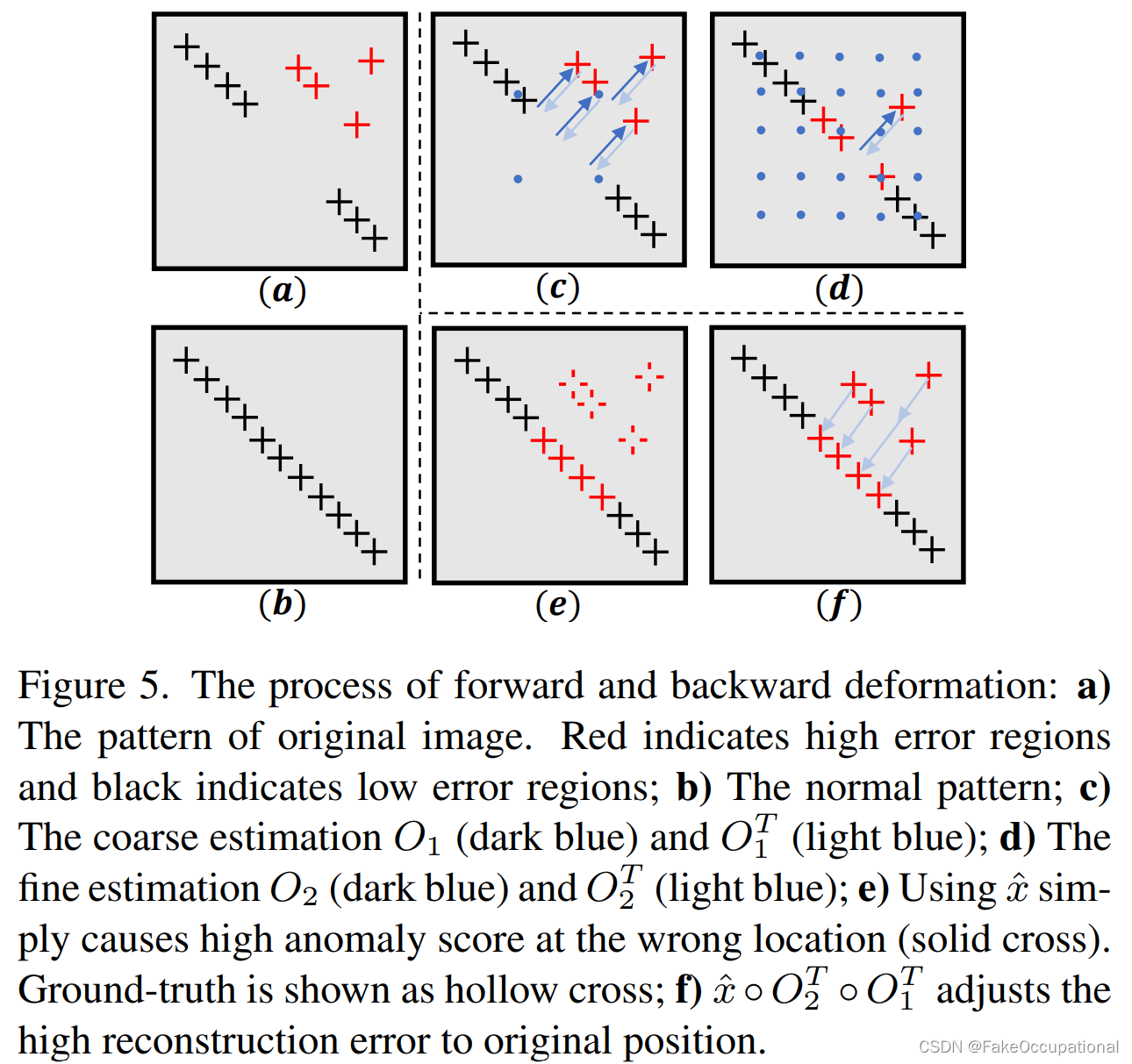
在这里插入图片描述

在这里插入图片描述

图5.前向和后向变形的过程： a）原始图像的图案。红色表示高误差区域，黑色表示低误差区域;b）正常模式;c）粗估计O（深蓝色）和O（浅蓝色）;d）精细估计O（深蓝色）和O（浅蓝色）;e）使用 ˆx 只会导致错误位置（实线叉）的高异常分数。地面实况显示为空心十字架;f） ˆx ◦ O◦ O将高重构误差调整到原始位置。

图像级异常得分和像素级异常得分分别计算如下：

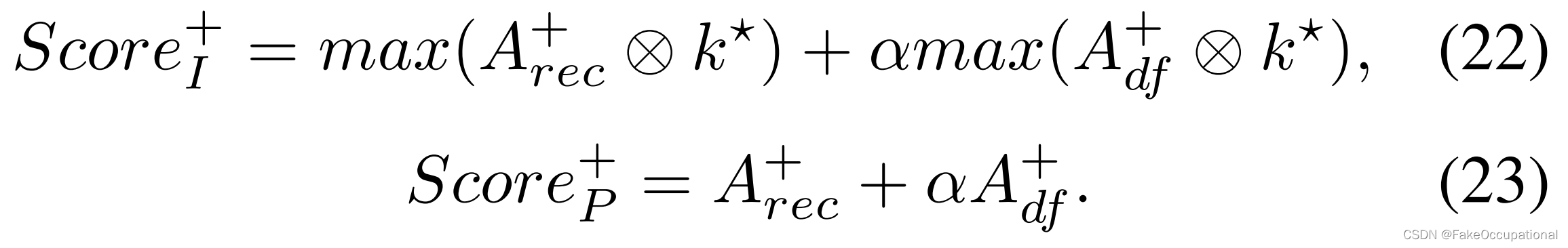
在这里插入图片描述

4. Experiments and Analysis

首先，我们在MNIST上进行了玩具实验，以说明我们的方法。然后，分别在视频异常检测和工业表面缺陷检测中报告了两个版本的DMAD框架的定量和定性结果。最后，我们进行了消融实验并分析了结果。

4.1. 数据集

监控视频。 Ped2 [27]、Avenue [23] 和 ShanghaiTech [25] 是固定视图视频。异常包括驾驶、骑自行车、跑步、扔东西等。在这些数据集中，相互遮挡、类似异常的行为、受污染的数据和不同的场景频繁出现。

工业图像。MVTec [2] 包含 15 种类型的工业图像，分为 5 种纹理和 10 种对象。缺陷包括裂纹、划痕等。普通工件有不同的位置、角度和纹理。它用于检测和定位任务。

4.2. 玩具实验

如图 6 所示，作者在 MNIST 数据集 [16] 上进行了toy实验，其设置类似于分布外（OOD）检测（即对“1、3、5、7、9”进行训练，并在所有类上进行测试）。我们的模型为每个数字类别搜索单独的内存项，以将其重建为特定于类的参考，并使用 PDM 中的变形场对其进行分层调整。
在这里插入图片描述

图6.实验的可视化。最后三行是：从内存重建的示例、粗变形后的示例和应用精细变形后的最终输出示例。

相比之下，没有多样性感知模块的记忆网络无法保证类内紧凑性和重构多样性，导致模型错误地获得数据集最优的“平均内存”，导致模糊重构和判别能力降低。采用全通道跳跃连接的模型存在捷径学习并成功重构异常的问题，削弱了识别异常的能力。

4.3. 实现细节

输入图像的大小调整为 256 × 256，并归一化为 [−1， 1] 范围内的值。根据帧填充策略[19]，视频异常检测的历史记录长度设置为4，图像的历史记录长度设置为0。PDM和PPDM通过堆叠stride-2卷积层获得不同的头。然后，我们使用T anh作为输出层的激活函数和裁剪函数，以确保变形值在[−1,1]之间。除非另有说明，否则自动编码器的架构分别符合 PDM 和 PPDM 的 MNAD [29] 和 RD [6] 的设置。方程（10）中的函数Dis（·）是样本空间重建的M SE损失和Grad损失以及深层特征的COS损失的组合。我们将 PDM 设置为（γ， γ） = （1， 0.25），PPDM 为（1， 1）（γ在第 4.5 节中讨论），β = 0.25，如 [35] 所示。在后处理过程中，我们对监控视频使用平均核，对工业图像使用高斯核，σ = 4，如[6]所示。采用帧差分法去除Avenue的静态异常，因为我们的方法检测了[23]中可能标记为正常异常的所有异常。我们使用方程（9）中计算的掩码来归一化[25]中由于尺度变化而导致的异常映射。此外，我们为三个视频任务设置了 α = 0.2，并为缺陷检测设置了一个附加选项 α = 0.05，具体取决于缺陷是否包含几何变化。该模型由AdamW[21]优化，学习率分别为2e-4和5e-3，如[6,29]所示，采用余弦退火LR[22]策略衰减。MNIST、Ped2、Avenue、Shanghai和MVTec分别采用60、60、60、10、400个epoch，批量大小为8。

4.4. 主要结果

监控视频。作者在表1中将本文的方法与SOTA在视频异常检测方面的工作进行了比较。即使既不使用外部估计器，也不删除训练数据中的异常帧，我们的方法也优于比较方法。此外，如果我们在[23]中检测到相机抖动的全局偏移，将有额外的0.1%增益。

在这里插入图片描述

定性结果如图7所示，a）原始图像;b）具有跳过连接的存储网络 ;c）带有VQLayer的PDM ;d）带有 ICM 的 PDM。绿框表示负数，红框表示正数，黄框表示弱正数。我们发现：（b）中的异常被过度重构;在（c）中，正常样本重建得不好;（d）大大改善了正常重建，对异常的抑制能力略低。

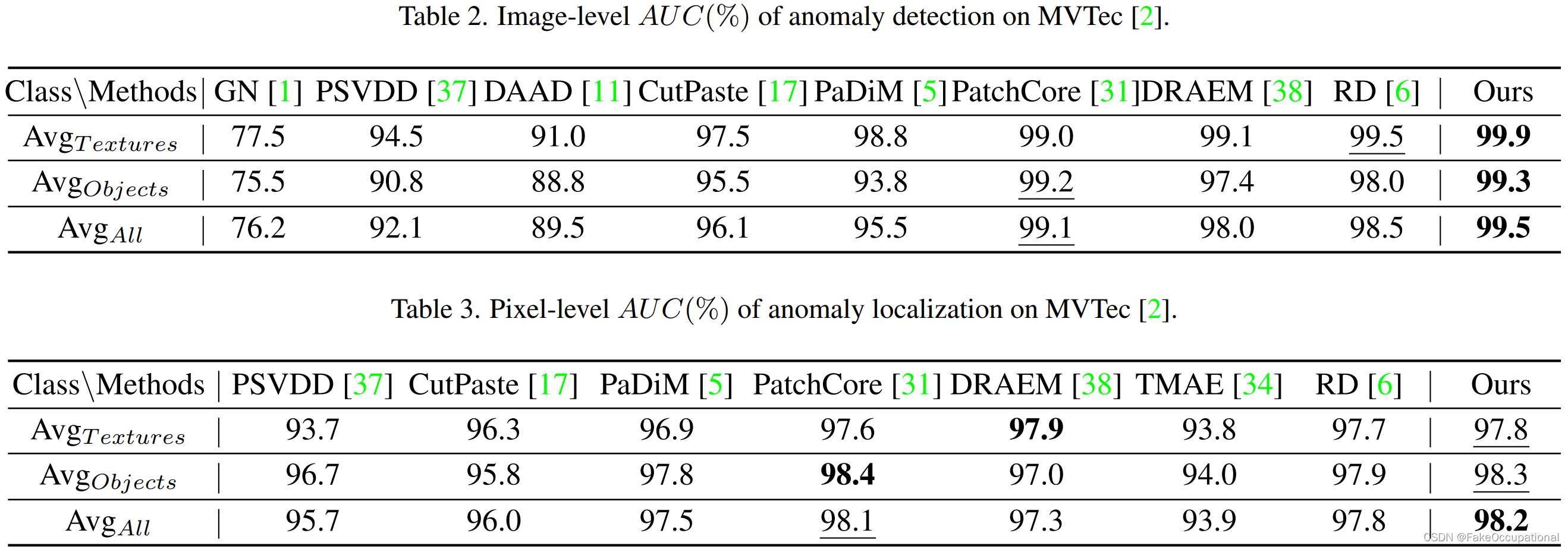
在这里插入图片描述

工业图像。 MVTec 上的异常检测结果如表 2 所示，像素级定位结果如表 3 所示。通过PPDM的变形，可以高性能地检测纹理异常，并且我们的方法在检测和定位任务中都优于SOTA方法，而无需从训练数据中存储大量嵌入。

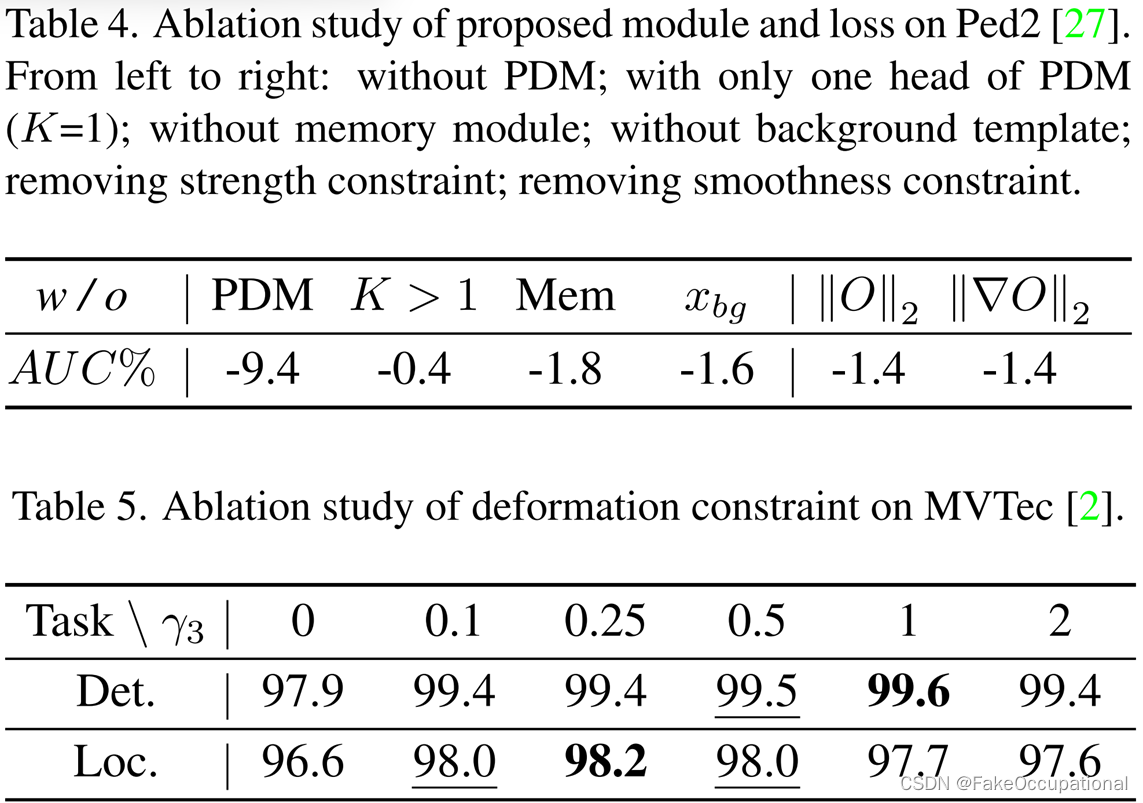
在这里插入图片描述

4.5. 消融研究

在这里插入图片描述

如表4所示，不带PDM的单输出存储器模块严重抑制了各种正常模式，而不带存储器的单独PDM提供了与以前的SOTA相当的性能提升，因为模块“Comp.”用作信息压缩模块。多尺度变形场的数量对性能的影响也不大。我们建议
K“至少应使控制网格比例覆盖表1。Ped2 [27]、Avenue [23] 和 Shanghai [25] 的视频异常检测结果。我们计算所有帧的AU C（%）。粗体数字表示最佳性能，带下划线的数字表示次优性能。表示由于性能较高或未实现而重现结果。

基本元素的大小（例如行人肢体）。此外，前景-背景选择模块进一步提高了内存嵌入的紧凑性。此外，如果缺少 PDM 的任何约束，异常信息将被传输并导致快捷学习。特别是，循环一致性约束Li也是PPDM避免退化解（−1.7%）的必要部分，因为通过消除所有必要的信息可以最小化特征重构误差。

如表5所示，所提方法对方程（19）中的超参数γ具有鲁棒性。在不形成简并解的条件下，弱化约束使模型更容易从细节较少的参考中恢复图像，并通过将异常转换为正常模式来更准确地感知异常的位置，这有利于定位任务。相反，加强约束可以缓解快捷方式学习，并通过保留更多的异常细节来改善图像级结果。

这篇关于OOD : DMAD Diversity-Measurable Anomaly Detection的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！