国密算法 SM9 公钥加密 数字签名 密钥交换 基于身份的密码算法（IBC）完整高效的开源python代码

上篇文章（发布于2023-09-18）给自己挖了个坑，说是要搞定SM9。从国庆前一周开始，到现在一个月时间，这个坑终于填上了。此前信息安全数学基础太差，理解不了SM9双线性对、扩域计算等等，为此还特意选修了现代密码学和近世代数2门专业课，边写代码边上课，带着问题学确实收获不少。说实话，弯路比预想的多，但实现效果却出乎意料的好。

SM9原理就不赘述了。目前，互联网上开源的基于Python原生实现的、确保正确（输出数据与《GBT 38635.2-2020 信息安全技术 SM9标识密码算法 第2部分：算法》附录A列举的数据完全一致）的SM9貌似是没有（我没找到）。我参考了以下代码： 

1. GitHub - gongxian-ding/gmssl-Python: a Python crypto for sm2/sm3/sm4/sm9
2. GitHub - guanzhi/GmSSL: 支持国密SM2/SM3/SM4/SM9/SSL的密码工具箱
3. GitHub - funfungho/GmSSL: http://gmssl.org/ v2.5.4
4. GitHub - GmSSL/GmSSL-Python: Python binding to the GmSSL library
5. GitHub - yaoyuanyylyy/abestudy: Study project for sm9, IBE, ABE implements with JPBC and BC under IDEA

其中，代码①应该是搬运了国外的IBC算法或有限域等运算的Python代码来尝试实现 SM9，虽然其实现并不完全正确，但给了我最初的重要参考。代码②③是C语言实现的GmSSL库，②是新版（还包含js代码实现的版本）包含更多数学上的优化，③是旧版但跟国标描述的更接近。代码④是代码②在Python下的调用，需要先编译②，我还没尝试过，应该是Python环境下最高效的，但没有基于Python原生实现SM9。代码⑤是SM9的Java实现，还有完整的SM9国标PDF。在GitHub上还能搜到不少，没下载的就不列举了。

本次用Python实现SM9国标描述的公钥加密、数字签名、密钥交换算法，除了保证正确性之外，还对实现细节做了若干数学和代码实现上的优化（包括但不限于：用2-NAF优化Miller循环和常数t模幂、最终模幂分解优化、用共轭实现frobenius映射、将Miller循环中的分子分母分别计算以减少模逆、针对Fq4零元较多而设计稀疏乘法、分圆循环子群Gϕ6(Fp2)下平方运算的优化、用Karatsuba 思想方法减少乘法）。不止是把他人的研究成果写进代码，也有自己独创的优化。另有些文章描述的优化方法在理论上是没问题的，但用Python实际实现却效果不佳，这些都要通过大量的代码测试来甄别。最后在不依赖第三方库的情况下，凝练成总计不到700行代码，我相信高效的代码一定不会太冗长。除了SM9国标，还参考了以下论文，在此对作者表示衷心感谢！

[1] 胡芯忆,何德彪,彭聪,等. 一种SM9算法R-ate对的快速实现方法[J]. 密码学报,2022,9(5):936-948. DOI:10.13868/j.cnki.jcr.000559.

[2] 甘植旺,廖方圆. 国密SM9中R-ate双线性对快速计算[J]. 计算机工程,2019,45(6):171-174. DOI:10.19678/j.issn.1000-3428.0054123.

[3] 王明东,何卫国,李军,等. 国密SM9算法R-ate对计算的优化设计[J]. 通信技术,2020,53(9):2241-2244. DOI:10.3969/j.issn.1002-0802.2020.09.025.

[4] 王江涛,樊荣,黄哲. SM9中高次幂运算的快速实现方法[J]. 计算机工程,2023,49(9):118-124,136. DOI:10.19678/j.issn.1000-3428.0065618.

[5] 付柱. R-ate双线性对密码算法的高效实现[D]. 天津:天津大学,2017.

[6] 孙铭玮. SM9标识密码算法关键技术研究[D]. 黑龙江:哈尔滨理工大学,2022.

[7] 李江峰. SM9算法的研究与FPGA实现[D]. 西安:西安电子科技大学,2021.

总之，非常感谢前辈们的工作，没有这些参考，对于一个非密码专业的网安学生，我手上连一本能讲清SM9具体实现的书都没有，想做出自己的实现更是难上加难，事实上这一个月我也的确走了很多弯路。不像SM2、SM3、SM4、ZUC对着国标或教材的算法描述就能实现，SM9涉及的数学基础要厚实得多，把图书馆里椭圆曲线的书都借遍了，它们和国标描述差不多，数学上都是那么几条式子，可这其中暗藏着巨大的知识鸿沟，让我对代码实现一时无从下手。另一个困难，是手上没有已经正确实现的Python代码（写惯了Python再来看Java会感觉代码太散，看C语言就像是当初学了C看汇编语言的感觉。当然，再难也要啃下来）。做其他国密算法实现的时候，更像是在优化，因为前人已经正确实现了，我只是研究如何把性能往上提，只要哪个步骤输出数据跟参考代码不一致，就说明实现错了，方便及时纠正。但做SM9实现，没有Python下的正确参考，双线性对有那么多复杂步骤，任何一步理解错了或一个粗心，都得不到正确结果，还不知道错在哪…………………………………………直到上周五突然输出了正确结果。再经过近一周优化，达到了满意的效果，及时将代码分享出来。 

废话多了，上源码：

from random import randrange
from math import ceil
from .SM3 import digest as sm3# SM9总则(GB_T 38635.1-2020) A.1 系统参数
q = 0XB640000002A3A6F1D603AB4FF58EC74521F2934B1A7AEEDBE56F9B27E351457D  # 基域特征
N = 0XB640000002A3A6F1D603AB4FF58EC74449F2934B18EA8BEEE56EE19CD69ECF25  # 群的阶
# 群G1的生成元 P1=(x_p1, y_p1)
x_p1 = 0X93DE051D62BF718FF5ED0704487D01D6E1E4086909DC3280E8C4E4817C66DDDD
y_p1 = 0X21FE8DDA4F21E607631065125C395BBC1C1C00CBFA6024350C464CD70A3EA616
# 群G2的生成元 P2=(x_p2, y_p2)
x_p2 = (0X85AEF3D078640C98597B6027B441A01FF1DD2C190F5E93C454806C11D8806141,0X3722755292130B08D2AAB97FD34EC120EE265948D19C17ABF9B7213BAF82D65B)
y_p2 = (0X17509B092E845C1266BA0D262CBEE6ED0736A96FA347C8BD856DC76B84EBEB96,0XA7CF28D519BE3DA65F3170153D278FF247EFBA98A71A08116215BBA5C999A7C7)
HASH_SIZE = 32  # sm3输出256位（32字节）
N_SIZE = 32  # 阶的字节数
KEY_LEN = 128  # 默认密钥位数
K2_len = 256  # MAC函数中密钥K2的位数def to_byte(x, size=None):if type(x) is int:return x.to_bytes(size if size else ceil(x.bit_length() / 8), byteorder='big')elif type(x) in (str, bytes):x = x.encode() if type(x) is str else xreturn x[:size] if size and len(x) > size else x  # 超过指定长度，则截取左侧字符elif type(x) in (tuple, list):return b''.join(to_byte(c, size) for c in x)return bytes(x)[:size] if size else bytes(x)# 将字节转换为int
def to_int(byte):return int.from_bytes(byte, byteorder='big')# 广义的欧几里得除法求模逆（耗时约为slow/SM2代码内get_inverse函数的43%）
def mod_inv(a, mod=q):if a == 0:return 0lm, low, hm, high = 1, a % mod, 0, modwhile low > 1:r = high // lowlm, low, hm, high = hm - lm * r, high - low * r, lm, lowreturn lm % modclass FQ:def __init__(self, n):self.n = ndef __add__(self, other):return FQ(self.n + other.n)def __sub__(self, other):return FQ(self.n - other.n)def __mul__(self, other):  # 右操作数可为intreturn FQ(self.n * (other.n if type(other) is FQ else other) % q)def __truediv__(self, other):  # 右操作数可为intreturn FQ(self.n * mod_inv(other.n if type(other) is FQ else other) % q)def __pow__(self, other):  # 操作数应为intreturn FQ(pow(self.n, other, q) if other else 1)def __eq__(self, other):  # 右操作数可为intreturn self.n % q == (other.n if type(other) is FQ else other) % qdef __neg__(self):return FQ(-self.n)def __repr__(self):return 'FQ(%064X)' % (self.n % q)def __bytes__(self):return to_byte(self.n % q, N_SIZE)def is_zero(self):return self.n % q == 0def inv(self):return FQ(mod_inv(self.n))def sqr(self):return FQ(self.n * self.n % q)@classmethoddef one(cls):return cls(1)@classmethoddef zero(cls):return cls(0)class FQ2:def __init__(self, *coeffs):  # 国标中的表示是高位在前，而此处coeffs是低位在前self.coeffs = coeffsdef __add__(self, other):(a0, a1), (b0, b1) = self.coeffs, other.coeffsreturn FQ2(a0 + b0, a1 + b1)def __sub__(self, other):(a0, a1), (b0, b1) = self.coeffs, other.coeffsreturn FQ2(a0 - b0, a1 - b1)def sqr(self):a0, a1 = self.coeffsreturn FQ2((a0 * a0 - (a1 * a1 << 1)) % q, (a0 * a1 << 1) % q)  # (a0^2 - 2 * a1^2, 2 * a0 * a1)def sqr_u(self):a0, a1 = self.coeffsreturn FQ2(-(a0 * a1 << 2) % q, (a0 * a0 - (a1 * a1 << 1)) % q)  # (-4 * a0 * a1, a0^2 - 2 * a1^2)def mul_b_u(self, b):  # 带参数乘法(a0, a1), (b0, b1) = self.coeffs, b.coeffsreturn FQ2(-(a0 * b1 + a1 * b0 << 1) % q, (a0 * b0 - (a1 * b1 << 1)) % q)  # (-2*(a0*b1+a1*b0), a0*b0-2*a1*b1)def __mul__(self, other):if type(other) is int:a0, a1 = self.coeffsreturn FQ2(a0 << 1, a1 << 1) if other == 2 else FQ2(a0 * other % q, a1 * other % q)(a0, a1), (b0, b1) = self.coeffs, other.coeffsa0b0, a1b1 = a0 * b0, a1 * b1  # Karatsuba 思想方法（节约一次乘法），实测此处约有5%提升，用在其他地方未见性能提升return FQ2((a0b0 - (a1b1 << 1)) % q, ((a0 + a1) * (b0 + b1) - (a0b0 + a1b1)) % q)  # (a0*b0-2*a1*b1,a0*b1+a1*b0)def __rmul__(self, other):return self.__mul__(other)def __truediv__(self, other):if type(other) is int:other_inv = mod_inv(other)return FQ2([c * other_inv % q for c in self.coeffs])return self * other.inv()def __pow__(self, other):  # 实际运行此函数的对象都是分圆循环子群Gϕ6(Fp2)中的元素if other == 0:return self.one()t = selffor ri in bin(other)[3:]:t = t.sqr2() * self if ri == '1' else t.sqr2()return tdef inv(self):a0, a1 = self.coeffsif a0 == 0:return FQ2(0, -mod_inv(a1 << 1))  # (0, -(2 * a1)^-1)if a1 == 0:return FQ2(mod_inv(a0), 0)  # (a0^-1, 0)k = mod_inv(a0 * a0 + (a1 * a1 << 1))  # k = (a0^2 + 2 * a1^2)^-1return FQ2(a0 * k % q, -a1 * k % q)  # (a0 * k, -a1 * k)def conjugate(self):  # 共轭a0, a1 = self.coeffsreturn self.__class__(a0, -a1)def get_fp_list(self):  # 返回所有基域元素（高位在前）if type(self) is FQ2:return [i % q for i in self[::-1]]return [y for x in self[::-1] for y in x.get_fp_list()] if self.coeffs else [0] * 4  # 注意FQ4对象零值的处理def __repr__(self):return '%s(%s)' % (self.__class__.__name__, ', '.join('%064X' % i for i in self.get_fp_list()))def __bytes__(self):  # 字节串高位在前return to_byte(self.get_fp_list(), N_SIZE)def __eq__(self, other):return self.get_fp_list() == other.get_fp_list()def __neg__(self):return self.__class__(*[-c for c in self.coeffs])def __getitem__(self, item):return self.coeffs[item]def is_zero(self):return all(c % q == 0 for c in self.coeffs) if type(self) is FQ2 else all(c.is_zero() for c in self.coeffs)@classmethoddef one(cls):return FQ2_one if cls is FQ2 else (FQ12_one if cls is FQ12 else FQ4_one)@classmethoddef zero(cls):return FQ2_zero if cls is FQ2 else ()class FQ4(FQ2):  # 零元的coeffs为空，可优化FQ12稀疏乘法运算def __add__(self, other):if not self.coeffs:return otherif not other.coeffs:return self(a0, a1), (b0, b1) = self.coeffs, other.coeffsreturn FQ4(a0 + b0, a1 + b1)def __sub__(self, other):if not self.coeffs:return -otherif not other.coeffs:return self(a0, a1), (b0, b1) = self.coeffs, other.coeffsreturn FQ4(a0 - b0, a1 - b1)def sqr(self):if not self.coeffs:return FQ4_zeroa0, a1 = self.coeffsreturn FQ4(a0.sqr() + a1.sqr_u(), a0 * a1 * 2)  # (a0^2 + a1^2 * u, 2 * a0 * a1)def sqr_v(self):if not self.coeffs:return FQ4_zeroa0, a1 = self.coeffsreturn FQ4(a0.mul_b_u(a1) * 2, a0.sqr() + a1.sqr_u())  # (2 * a0 * a1 * u, a0^2 + a1^2 * u)def mul_b_v(self, b):  # 带参数乘法if not self.coeffs or not b.coeffs:return FQ4_zero(a0, a1), (b0, b1) = self.coeffs, b.coeffsreturn FQ4(a0.mul_b_u(b1) + a1.mul_b_u(b0), a0 * b0 + a1.mul_b_u(b1))  # (a0*b1*u+a1*b0*u, a0*b0+a1*b1*u)def __mul__(self, other):if not self.coeffs:return FQ4_zeroif type(other) is int:a0, a1 = self.coeffsreturn FQ4(a0 * other, a1 * other)if not other.coeffs:return FQ4_zero(a0, a1), (b0, b1) = self.coeffs, other.coeffsreturn FQ4(a0 * b0 + a1.mul_b_u(b1), a0 * b1 + a1 * b0)  # (a0*b0+a1*b1*u, a0*b1+a1*b0)def inv(self):if not self.coeffs:return FQ4_zeroa0, a1 = self.coeffsk = (a1.sqr_u() - a0.sqr()).inv()return FQ4((-a0 * k), a1 * k)class FQ12(FQ2):def __add__(self, other):(a0, a1, a2), (b0, b1, b2) = self.coeffs, other.coeffsreturn FQ12(a0 + b0, a1 + b1, a2 + b2)def __sub__(self, other):(a0, a1, a2), (b0, b1, b2) = self.coeffs, other.coeffsreturn FQ12(a0 - b0, a1 - b1, a2 - b2)def sqr(self):a0, a1, a2 = self.coeffsreturn FQ12(a0.sqr() + a1.mul_b_v(a2) * 2, a0 * a1 * 2 + a2.sqr_v(), a0 * a2 * 2 + a1.sqr())def __mul__(self, other):(a0, a1, a2), (b0, b1, b2) = self.coeffs, other.coeffsreturn FQ12(a0 * b0 + a1.mul_b_v(b2) + a2.mul_b_v(b1), a0 * b1 + a1 * b0 + a2.mul_b_v(b2),a0 * b2 + a1 * b1 + a2 * b0)def sqr2(self):  # 分圆循环子群Gϕ6(Fp2)中的元素平方a, b, c = self.coeffsa2, b2, c2v = a.sqr(), b.sqr(), c.sqr_v()return FQ12(a2 + (a2 - a.conjugate()) * 2, c2v + (c2v + b.conjugate()) * 2, b2 + (b2 - c.conjugate()) * 2)def pow_t(self):  # 只可用于分圆循环子群Gϕ6(Fp2)中的元素，求逆为共轭c, _inv = self, self.frobenius6()for ti in t_NAF:c = c.sqr2()if ti == '1':c = c * selfelif ti == '2':  # 用2代替-1c = c * _invreturn cdef inv(self):a0, a1, a2 = self.coeffsa0_2, a1_2 = a0.sqr(), a1.sqr()if a2.is_zero():k = (a0 * a0_2 + a1.mul_b_v(a1_2)).inv()return FQ12(a0_2 * k, (-a0 * a1 * k), a1_2 * k)t0, t1, t2 = a1_2 - a0 * a2, a0 * a1 - a2.sqr_v(), a0_2 - a1.mul_b_v(a2)t3 = a2 * (t1.sqr() - t0 * t2).inv()return FQ12(t2 * t3, (-t1 * t3), t0 * t3)def frobenius(self):(a0, a1), (b0, b1), (c0, c1) = self.coeffsa = FQ4(a0.conjugate(), a1.conjugate() * alpha3)b = FQ4(b0.conjugate() * alpha1, b1.conjugate() * alpha4)c = FQ4(c0.conjugate() * alpha2, c1.conjugate() * alpha5)return FQ12(a, b, c)def frobenius2(self):a, b, c = self.coeffsreturn FQ12(a.conjugate(), b.conjugate() * alpha2, c.conjugate() * alpha4)def frobenius3(self):(a0, a1), (b0, b1), (c0, c1) = self.coeffsa = FQ4(a0.conjugate(), -a1.conjugate() * alpha3)b = FQ4(b0.conjugate() * alpha3, b1.conjugate())c = FQ4(-c0.conjugate(), c1.conjugate() * alpha3)return FQ12(a, b, c)def frobenius6(self):a, b, c = self.coeffsreturn FQ12(a.conjugate(), -b.conjugate(), c.conjugate())class ECC_Point:def __init__(self, *pt):  # 采用Jacobian射影坐标计算，输入仿射坐标后会转换为Jacobian射影坐标self.pt = pt if len(pt) == 3 else (*pt, pt[0].one())@classmethoddef from_byte(cls, byte):  # 输入bytes类型仿射坐标，构建点对象fp_num = len(byte) // (N_SIZE << 1)  # 单个坐标包含的域元素个数if fp_num in (1, 2) and len(byte) % N_SIZE == 0:fp_list = [to_int(byte[i:i + N_SIZE]) for i in range(0, len(byte), N_SIZE)]  # 将bytes转换为域元素列表if fp_num == 1:return cls(FQ(fp_list[0]), FQ(fp_list[1]))x_list, y_list = fp_list[fp_num - 1::-1], fp_list[:fp_num - 1:-1]  # 从bytes到FQ2对象保存的域元素，需翻转高低位顺序return cls(FQ2(*x_list), FQ2(*y_list))return Falsedef is_inf(self):return self[2].is_zero()def is_on_curve(self):  # 检查点是否满足曲线方程 y^2 == x^3 + bx, y, z = self.ptreturn y ** 2 == x ** 3 + (_b1 if type(x) is FQ else _b2) * z ** 6def double(self):x, y, z = self.ptT1, _y2 = x.sqr() * 3, y.sqr()T2, T3 = x * _y2 * 4, _y2.sqr() * 8x3 = T1.sqr() - T2 * 2y3 = T1 * (T2 - x3) - T3z3 = y * z * 2return ECC_Point(x3, y3, z3)def zero(self):cls = self[0].__class__return ECC_Point(cls.one(), cls.one(), cls.zero())def __add__(self, p2):if self.is_inf():return p2if p2.is_inf():return self(x1, y1, z1), (x2, y2, z2) = self.pt, p2.ptz1_2, z2_2 = z1.sqr(), z2.sqr()T1, T2 = x1 * z2_2, x2 * z1_2T3, T4, T5 = T1 - T2, y1 * z2_2 * z2, y2 * z1_2 * z1T6, T7, T3_2 = T4 - T5, T1 + T2, T3.sqr()T8, T9 = T4 + T5, T7 * T3_2x3 = T6.sqr() - T9T10 = T9 - x3 * 2y3 = (T10 * T6 - T8 * T3_2 * T3) * _2_invz3 = z1 * z2 * T3return ECC_Point(x3, y3, z3)def multiply(self, n):  # 算法一：二进制展开法if n in (0, 1):return self if n else self.zero()Q = selffor i in bin(n)[3:]:Q = Q.double() + self if i == '1' else Q.double()return Qdef __mul__(self, n):  # 算法三：滑动窗法k = bin(n)[2:]l, r = len(k), 5  # 滑动窗口为5效果较好if r >= l:  # 如果窗口大于k的二进制位数，则本算法无意义return self.multiply(n)P_ = {1: self, 2: self.double()}  # 保存P[j]值的字典for i in range(1, 1 << (r - 1)):P_[(i << 1) + 1] = P_[(i << 1) - 1] + P_[2]t = rwhile k[t - 1] != '1':t -= 1hj = int(k[:t], 2)Q, j = P_[hj], twhile j < l:if k[j] == '0':Q = Q.double()j += 1else:t = min(r, l - j)while k[j + t - 1] != '1':t -= 1hj = int(k[j:j + t], 2)Q = Q.multiply(1 << t) + P_[hj]j += treturn Qdef __rmul__(self, n):return self.__mul__(n)def __eq__(self, p2):(x1, y1, z1), (x2, y2, z2) = self.pt, p2.ptz1_2, z2_2 = z1.sqr(), z2.sqr()return x1 * z2_2 == x2 * z1_2 and y1 * z2_2 * z2 == y2 * z1_2 * z1def __neg__(self):x, y, z = self.ptreturn ECC_Point(x, -y, z)def __getitem__(self, item):return self.pt[item]def __repr__(self):return '%s%s' % (self.__class__.__name__, self.normalize())def __bytes__(self):return to_byte(self.normalize())def normalize(self):x, y, z = self.ptif not hasattr(self, 'normalize_tuple'):if z != z.one():z_inv = z.inv()z_inv_2 = z_inv.sqr()x, y = x * z_inv_2, y * z_inv_2 * z_invself.normalize_tuple = (x.n, y.n) if type(x) is FQ else (x, y)return self.normalize_tupledef frobenius(self):x, y, z = self.ptreturn ECC_Point(x.conjugate(), y.conjugate(), z.conjugate() * alpha1)def frobenius2_neg(self):x, y, z = self.ptreturn ECC_Point(x, -y, z * alpha2)FQ2_one, FQ2_zero = FQ2(1, 0), FQ2(0, 0)  # FQ2单位元、零元
FQ4_one, FQ4_zero = FQ4(FQ2_one, FQ2_zero), FQ4()  # FQ4单位元、零元
FQ12_one = FQ12(FQ4_one, FQ4_zero, FQ4_zero)  # FQ12单位元
P1 = ECC_Point(FQ(x_p1), FQ(y_p1))  # 群G1的生成元
P2 = ECC_Point(FQ2(*x_p2[::-1]), FQ2(*y_p2[::-1]))  # 群G2的生成元
_b1, _b2 = FQ(5), FQ2(0, 5)  # b2=βb=(1,0)*5
alpha1 = 0X3F23EA58E5720BDB843C6CFA9C08674947C5C86E0DDD04EDA91D8354377B698B  # -2^((q - 1)/12)
alpha2 = 0XF300000002A3A6F2780272354F8B78F4D5FC11967BE65334  # -2^((q - 1)/6)
alpha3 = 0X6C648DE5DC0A3F2CF55ACC93EE0BAF159F9D411806DC5177F5B21FD3DA24D011  # -2^((q - 1)/4)
alpha4 = 0XF300000002A3A6F2780272354F8B78F4D5FC11967BE65333  # -2^((q - 1)/3)
alpha5 = 0X2D40A38CF6983351711E5F99520347CC57D778A9F8FF4C8A4C949C7FA2A96686
_2_inv = 0X5B2000000151D378EB01D5A7FAC763A290F949A58D3D776DF2B7CD93F1A8A2BF  # 1/2
_3div2 = 0X5B2000000151D378EB01D5A7FAC763A290F949A58D3D776DF2B7CD93F1A8A2C0  # 3/2
R_ate_a_NAF = '00100000000000000000000000000000000000010001020200020200101000020'  # a=6t+2的二进制非相邻表示(2-NAF)（去首1）
t_NAF = '10000000000000000000000000000000000000102020010000201020001010'  # t的二进制非相邻表示(2-NAF)（去首1）
hlen = 320  # 8 * ceil(5 * log(N, 2) / 32)# 线函数g T,Q(P)，求过点T和Q的直线在P上的值（分母在最终模幂时值为1，可消去）
def g(T, Q, P=None):if P:(xT, yT, zT), (xQ, yQ, zQ), (xP, yP) = T, Q, PzT_2, zQ_2 = zT.sqr(), zQ.sqr()zQ_3, t1 = zQ * zQ_2, (xT * zQ_2 - xQ * zT_2) * zT * zQb1, t2 = t1 * zQ_3, (yT * zQ_3 - yQ * zT * zT_2) * zQa0, a4 = t1 * yQ - t2 * xQ, t2 * zQ_2 * xPelse:  # 当P为空时，g T,T(P)，求过点T的切线在P上的值(xT, yT, zT), (xP, yP) = T, QzT_2, t1 = zT.sqr(), xT.sqr() * _3div2b1, a0, a4 = zT * zT_2 * yT, yT.sqr() - t1 * xT, t1 * zT_2 * xPreturn FQ12(FQ4(a0, -b1 * yP), FQ4_zero, FQ4(a4, FQ2_zero))# BN曲线上R_ate对的计算
def e(P, Q):T, nQ, f, P_xy = Q, -Q, FQ12_one, P.normalize()for ai in R_ate_a_NAF:f, T = f.sqr() * g(T, P_xy), T.double()if ai == '1':f, T = f * g(T, Q, P_xy), T + Qelif ai == '2':  # 用2代替-1f, T = f * g(T, nQ, P_xy), T + nQQ1, nQ2 = Q.frobenius(), Q.frobenius2_neg()return final_exp(f * g(T, Q1, P_xy) * g(T + Q1, nQ2, P_xy))# 最终模幂
def final_exp(f):m = f.frobenius6() * f.inv()  # f^(p^6 - 1)s = m.frobenius2() * m  # m^(p^2 + 1)# 困难部分 s^(p^3 + (6t^2+1)p^2 + (-36t^3-18t^2-12t+1)p + (-36t^3-30t^2-18t-2))s_6t = s.pow_t() ** 6s_6t2, s_12t = s_6t.pow_t(), s_6t.sqr2()s_6t3, s_12t2, s_18t = s_6t2.pow_t(), s_6t2.sqr2(), s_6t * s_12ts_36t3, s_18t2, a2 = s_6t3 ** 6, s_6t2 * s_12t2, s_6t2 * ss_30t2, a1 = s_12t2 * s_18t2, (s_36t3 * s_18t2 * s_12t).frobenius6() * sa0 = (s_36t3 * s_30t2 * s_18t * s.sqr2()).frobenius6()return s.frobenius3() * a2.frobenius2() * a1.frobenius() * a0# SM9算法(GB_T 38635.2-2020) 5.3.6定义的密钥派生函数
# Z为bytes类型，klen表示输出密钥比特长度（8的倍数）；输出为bytes类型
def KDF(Z, klen=KEY_LEN):ksize, K = klen >> 3, bytearray()for ct in range(1, ceil(ksize / HASH_SIZE) + 1):K.extend(sm3(Z + to_byte(ct, 4)))return K[:ksize]# SM9算法(GB_T 38635.2-2020) 5.3.2.2和5.3.2.3定义的密码函数
def H(i, Z):Ha = to_int(KDF(to_byte(i, 1) + Z, hlen))return Ha % (N - 1) + 1# SM9算法(GB_T 38635.2-2020) 5.3.5定义的消息认证码函数
def MAC(K2, Z):return sm3(Z + K2)class SM9:  # SM9算法(GB_T 38635.2-2020)def __init__(self, ID='', ks=None, Ppub_s=None, ke=None, Ppub_e=None, hid_s=1, hid_e=3, is_KGC=False):self.ID = IDif is_KGC:  # 作为密钥生成中心self.ks = ks if ks and 0 < ks % N < N else randrange(1, N)  # 未提供签名主密钥则随机生成self.Ppub_s = Ppub_s if Ppub_s and Ppub_s == P2 * self.ks else P2 * self.ks  # 确保签名主公钥与签名主私钥匹配self.ke = ke if ke and 0 < ke % N < N else randrange(1, N)  # 未提供加密主密钥则随机生成self.Ppub_e = Ppub_e if Ppub_e and Ppub_e == P1 * self.ke else P1 * self.ke  # 确保加密主公钥与加密主私钥匹配else:  # 作为用户self.ds, self.Ppub_s, self.de, self.Ppub_e = ks, Ppub_s, ke, Ppub_eself.gs, self.ge = e(P1, Ppub_s), e(Ppub_e, P2)self.hid_s_byte, self.hid_e_byte = [hid if type(hid) is bytes else to_byte(hid, 1) for hid in [hid_s, hid_e]]def KGC_gen_user(self, ID):ID_byte = to_byte(ID)t1 = (H(1, ID_byte + self.hid_s_byte) + self.ks) % Nif t1 == 0:  # 需重新产生签名主密钥，并更新所有用户的签名密钥return Falset2 = self.ks * mod_inv(t1, N) % Nds = P1 * t2  # 用户签名私钥t1 = (H(1, ID_byte + self.hid_e_byte) + self.ke) % Nif t1 == 0:  # 需重新产生加密主密钥，并更新所有用户的加密密钥return Falset2 = self.ke * mod_inv(t1, N) % Nde = P2 * t2  # 用户加密私钥return SM9(ID, ds, self.Ppub_s, de, self.Ppub_e, self.hid_s_byte, self.hid_e_byte)# 6.2 数字签名生成算法def sign(self, M, r=None, outbytes=True):l = 0while l == 0:r = r if r else randrange(1, N)  # A2w = bytes(self.gs ** r)  # A3h = H(2, to_byte(M) + w)  # A4l = (r - h) % N  # A5S = self.ds * l  # A6return to_byte([h, S]) if outbytes else (h, S)# 6.4 数字签名验证算法def verify(self, ID, M_, sig):h_, S_ = (to_int(sig[:N_SIZE]), ECC_Point.from_byte(sig[N_SIZE:])) if type(sig) is bytes else sigif not 0 < h_ < N or not S_ or not S_.is_on_curve():  # B1、B2return Falset = self.gs ** h_  # B4h1 = H(1, to_byte(ID) + self.hid_s_byte)  # B5P = P2 * h1 + self.Ppub_s  # B6u = e(S_, P)  # B7w_ = bytes(u * t)  # B8h2 = H(2, to_byte(M_) + w_)  # B9return h_ == h2# A 发起协商（也可用作B生成rB、RB；outbytes=True时输出bytes）# 7.2 密钥交换协议 A1-A3def agreement_initiate(self, IDB, r=None, outbytes=True):QB = P1 * H(1, to_byte(IDB) + self.hid_e_byte) + self.Ppub_e  # A1rA = r if r else randrange(1, N)  # A2RA = QB * rA  # A3return rA, bytes(RA) if outbytes else RA# B 响应协商（option=True时计算选项部分）# 7.2 密钥交换协议 B1-B6def agreement_response(self, RA, IDA, option=False, rB=None, klen=KEY_LEN, outbytes=True):RA = ECC_Point.from_byte(RA) if type(RA) is bytes else RAif not RA or not RA.is_on_curve():  # B4return False, 'RA不属于椭圆曲线群G1'rB, RB = self.agreement_initiate(IDA, rB, outbytes)  # B1-B3g1, g2 = e(RA, self.de), bytes(self.ge ** rB)  # B4g1, g3 = bytes(g1), bytes(g1 ** rB)  # B4tmp_byte = to_byte([IDA, self.ID, RA, RB])SKB = KDF(tmp_byte + g1 + g2 + g3, klen)  # B5if not option:return True, (RB, SKB)self.tmp_byte2 = g1 + sm3(g2 + g3 + tmp_byte)SB = sm3(to_byte(0x82, 1) + self.tmp_byte2)  # B6（可选部分）return True, (RB, SKB, SB)# A 协商确认# 7.2 密钥交换协议 A5-A8def agreement_confirm(self, rA, RA, RB, IDB, SB=None, option=False, klen=KEY_LEN):RB = ECC_Point.from_byte(RB) if type(RB) is bytes else RBif not RB or not RB.is_on_curve():  # A5return False, 'RB不属于椭圆曲线群G1'g1_, g2_ = bytes(self.ge ** rA), e(RB, self.de)  # A5g2_, g3_ = bytes(g2_), bytes(g2_ ** rA)  # A5tmp_byte = to_byte([self.ID, IDB, RA, RB])if option and SB:  # A6（可选部分）tmp_byte2 = g1_ + sm3(g2_ + g3_ + tmp_byte)S1 = sm3(to_byte(0x82, 1) + tmp_byte2)if S1 != SB:return False, 'S1 != SB'SKA = KDF(tmp_byte + g1_ + g2_ + g3_, klen)  # A7if not option or not SB:return True, SKASA = sm3(to_byte(0x83, 1) + tmp_byte2)  # A8return True, (SKA, SA)# B 协商确认（可选部分）# 7.2 密钥交换协议 B8def agreement_confirm2(self, SA):if not hasattr(self, 'tmp_byte2'):return False, 'step error'S2 = sm3(to_byte(0x83, 1) + self.tmp_byte2)if S2 == SA:del self.tmp_byte2return True, ''return False, 'S2 != SA'# 8.2 密钥封装算法def encaps(self, IDB, klen, r=None, outbytes=True):K = bytes()while K == bytes(len(K)):r, C = self.agreement_initiate(IDB, r, outbytes)  # A1-A3w = bytes(self.ge ** r)  # A5K = KDF(to_byte([C, w, IDB]), klen)return K, C# 8.4 密钥封装算法def decaps(self, C, klen):C = ECC_Point.from_byte(C) if type(C) is bytes else Cif not C or not C.is_on_curve():  # B1return False, 'C不属于椭圆曲线群G1'w_ = bytes(e(C, self.de))  # B2K_ = KDF(to_byte([C, w_, self.ID]), klen)  # B3return (True, K_) if K_ != bytes(len(K_)) else (False, 'K为全0比特串')# 9.2 加密算法def encrypt(self, IDB, M, r=None, outbytes=True):M = to_byte(M)K, C1 = self.encaps(IDB, (len(M) << 3) + K2_len, r, outbytes)  # A1-A6.a.1K1, K2 = K[:len(M)], K[len(M):]  # A6.a.1C2 = bytes(M[i] ^ K1[i] for i in range(len(M)))  # A6.a.2C3 = MAC(K2, C2)  # A7return to_byte([C1, C3, C2]) if outbytes else (C1, C3, C2)# 9.4 解密算法def decrypt(self, C):C3_start, C3_end = N_SIZE << 1, (N_SIZE << 1) + HASH_SIZEC1, C3, C2 = (C[:C3_start], C[C3_start:C3_end], C[C3_end:]) if type(C) is bytes else Cres, K_ = self.decaps(C1, (len(C2) << 3) + K2_len)  # B1-B3.a.1if not res:return False, K_.replace('C', 'C1')K1_, K2_ = K_[:len(C2)], K_[len(C2):]  # B3.a.1if K1_ == bytes(len(K_)):return False, 'K1\'为全0比特串'u = MAC(K2_, C2)  # B4if u != C3:return False, 'u != C3'return True, bytes(C2[i] ^ K1_[i] for i in range(len(C2)))  # B3.a.2

使用时先创建KGC对象，由它生成用户对象，再由用户对象完成公钥加密、数字签名或密钥交换，例子如下：

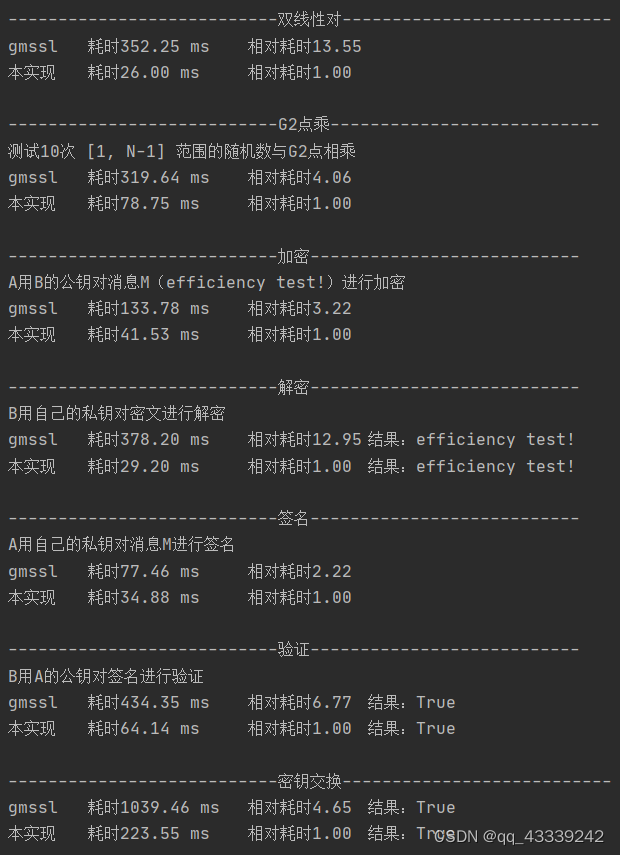
    IDA, IDB, message = 'Alice', 'Bob', 'Chinese IBS standard'kgc = SM9(ks=0x130E78459D78545CB54C587E02CF480CE0B66340F319F348A1D5B1F2DC5F4,ke=0x2E65B0762D042F51F0D23542B13ED8CFA2E9A0E7206361E013A283905E31F, is_KGC=True)sm9_A, sm9_B = kgc.KGC_gen_user(IDA), kgc.KGC_gen_user(IDB)assert bytes(sm9_A.gs).hex().swapcase().endswith('F0F071D7D284FCFB')print("-----------------test sign and verify---------------")r = 0x033C8616B06704813203DFD00965022ED15975C662337AED648835DC4B1CBEsignature = sm9_A.sign(message, r)assert signature.hex().swapcase().endswith('827CC2ACED9BAA05')assert sm9_B.verify(IDA, message, signature)print("success")print("-----------------test key agreement---------------")rA = 0x5879DD1D51E175946F23B1B41E93BA31C584AE59A426EC1046A4D03B06C8rA, RA = sm9_A.agreement_initiate(IDB, rA)  # A发起协商# A将RA发送给BrB = 0x018B98C44BEF9F8537FB7D071B2C928B3BC65BD3D69E1EEE213564905634FEres, content = sm9_B.agreement_response(RA, IDA, True, rB)  # B响应协商if not res:print('B报告协商错误：', content)returnRB, SKB, SB = content# B将RB、SB发送给Ares, content = sm9_A.agreement_confirm(rA, RA, RB, IDB, SB, True)  # A协商确认if not res:print('A报告协商错误：', content)returnSKA, SA = contentassert SKA.hex().swapcase() == '68B20D3077EA6E2B825315836FDBC633'# A将SA发送给Bres, content = sm9_B.agreement_confirm2(SA)  # B协商确认if not res:print('B报告协商错误：', content)returnassert SKA == SKBprint("success")print("-----------------test encrypt and decrypt---------------")message = 'Chinese IBE standard'kgc = SM9(ks=kgc.ks, Ppub_s=kgc.Ppub_s,ke=0x01EDEE3778F441F8DEA3D9FA0ACC4E07EE36C93F9A08618AF4AD85CEDE1C22, is_KGC=True)sm9_A, sm9_B = kgc.KGC_gen_user(IDA), kgc.KGC_gen_user(IDB)C = sm9_A.encrypt(IDB, message, 0xAAC0541779C8FC45E3E2CB25C12B5D2576B2129AE8BB5EE2CBE5EC9E785C)assert C.hex().swapcase().endswith('378CDD5DA9513B1C')res, content = sm9_B.decrypt(C)if not res:print('解密错误：', content)returnassert message == content.decode()print("success")

虽然和代码①实现的结果不一样，但手头也只有这一个Python的原生实现，但还是比较一下。

此前介绍国密算法的系列文章如下：

三篇SM2：

国密算法 SM2 公钥加密 数字签名 密钥交换 更高效、依赖更少的开源python代码_国密算法 开源-CSDN博客

国密算法 SM2 公钥加密 数字签名 密钥交换 全网最高效的开源python代码_-CSDN博客

国密算法 SM2 公钥加密 非对称加密 数字签名 密钥协商 python实现完整代码_qq_43339242的博客-CSDN博客_python sm2

SM3：国密算法 SM3 消息摘要 杂凑算法 哈希函数 散列函数 python实现完整代码_qq_43339242的博客-CSDN博客_国密sm3

SM4：国密算法 SM4 对称加密 分组密码 python实现完整代码_qq_43339242的博客-CSDN博客_python国密算法库

ZUC：国密算法 ZUC流密码 祖冲之密码 python代码完整实现_qq_43339242的博客-CSDN博客_国密算法代码

对上述几个算法和实现不了解的，建议点进去看看。下面这篇文章是对上述的汇总：

国密算法 SM2公钥密码 SM3杂凑算法 SM4分组密码 python代码完整实现_qq_43339242的博客-CSDN博客_python sm2

上述所有国密算法的完整Python实现代码和测试代码，库名叫hggm，托管在码云：hggm - 国密算法 SM2 SM3 SM4 python实现完整代码: 国密算法 SM2公钥密码 SM3杂凑算法 SM4分组密码 python代码完整实现 效率高于所有公开的python国密算法库 (gitee.com)

至此，公开国密算法的一家子（SM2、SM3、SM4、SM9和ZUC）已经团聚了，在国密算法Python原生实现领域，目前来看，性能应该都做到了网上开源最优。

咱们所处的世界还很不太平，建设网络安全强国的脚步一刻也不会停，任重道远。