深度学习在单线性回归方程中的应用--TensorFlow实战详解

本文主要是介绍深度学习在单线性回归方程中的应用--TensorFlow实战详解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

深度学习在单线性回归方程中的应用–TensorFlow实战详解

提到人工智能，绕不开的话题就是机器学习了，因为机器学习是人工智能很重要的一个分支。而今天要讨论的深度学习又是机器学习的一个很重要的分支。

目前的主流深度学习框架有

• TensorFlow
• Keras
• Theano
• …

1、人工智能<–>机器学习<–>深度学习

其实机器学习就是让机器自己学习的算法，我们需要训练出这个算法，在利用这个算法解决一些问题。机器学习和人工智能的关系就是，机器学习是技术，人工智能是概念，机器学习技术用来解决人工智能出现的问题。

显而易见的说，机器学习就是训练如下的一个模型，用这个模型解决问题，那么如何训练呢？那就是通过历史数据来训练。

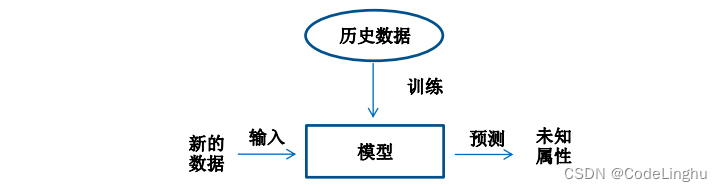
深度学习是机器学习的一个子集，深度学习是利用深度的神经网络，将模型处理得更为复杂，从而使模型对数据的理解更加深入。

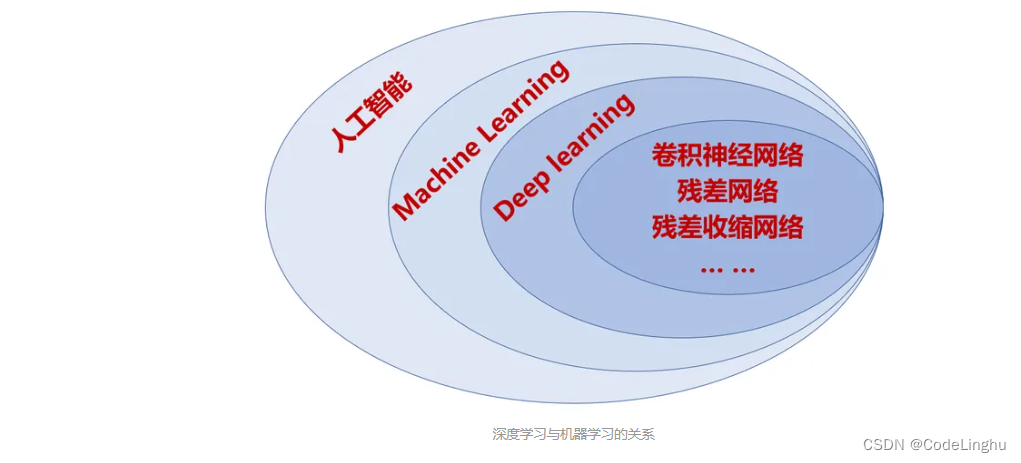
2、线性回归方程

首先要知道线性回归的概念，所谓回归是指：回归事物的本质和真相。线性是指通过一个已知条件x得到预测值y。我们中学学过的y=kx放在坐标系里讨论，就是一条直线，我们称其为：线性的。

所以线性回归方程我们可以抽象成如下：

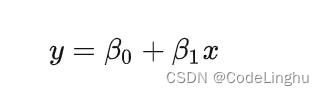
它的图象可以表示为：

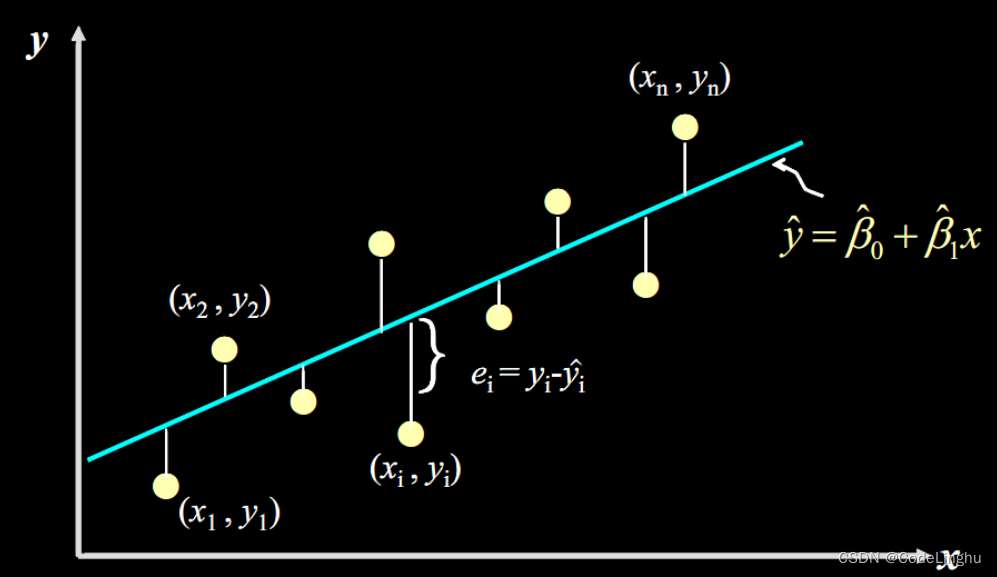
线性回归有一个特点就是，我们事先知道一个方程，然后代入x因变量，就可以得到y的值，只要我们知道这个方程，那么我们就掌握了预测未来的可能。在深度学习中，我们将x点成为 特征，将得到的y成为标签，而一堆特征我们称为 样本。

那么我们对一个模型的训练过程就如下图：

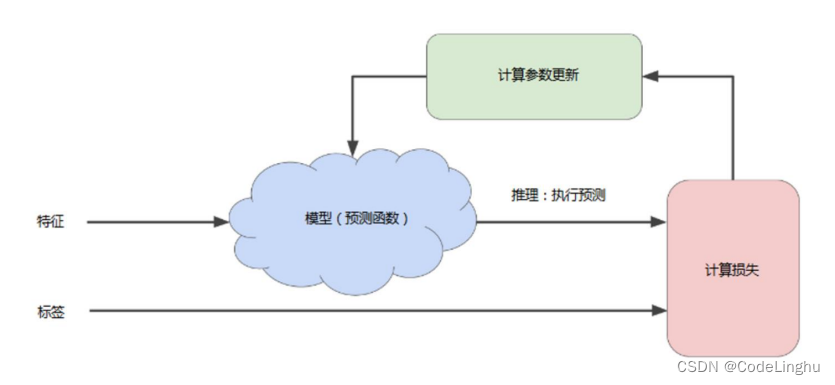
机器学习要做的事情是：先给你一些点，也就是数据集，我们通过这个数据集训练出一个方程，也就是一个模型，然后再用这个模型去预测未来。

3、TensorFlow实战解决单线性回归问题

首先我们要知道利用深度学习算法训练一个模型的核心步骤：

• 准备数据集
• 构建模型
• 训练模型
• 进行预测

我们这里选用了TensorFlow框架进行训练。

单变量线性回归方程可以表示如下：

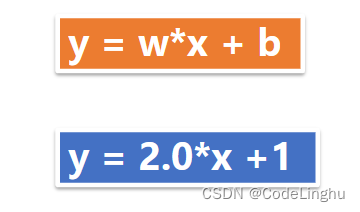
人工数据集生成

现在的已知条件是，我们有一堆点在这里，然后我们希望通过这些点找到上面的回归方程，这个回归方程就是我们说的模型，这个找方程的过程叫做：模型训练。方程找到了，也就是计算出了w和b了，那么我们就可以通过这个模型预测未知的y值了。

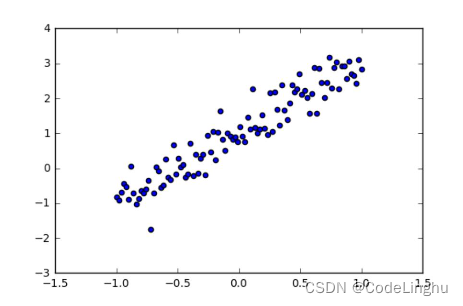
这些点我们可以通过随机生成人工数据集，为了让这些点均匀分布，不会分布在一条线上，我们还要加上噪音振幅。

# 图象实现
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import tensorflow.compat.v1 as tf
#关闭Eager Execution
tf.compat.v1.disable_eager_execution()
#设置随机数种子
np.random.seed(5)

然后生成100个点，每个点的取值在-1,1之间

x_data=np.linspace(-1,1,100)
# y=2x+1+噪声
y_data=2*x_data+1.0+np.random.randn(*x_data.shape)*0.4

利用matplotlib画出结果

# 画出随机数生成的散点图
plt.scatter(x_data,y_data)
# 画出我们的目标，也就是希望得到的函数y=2*x+1
plt.plot(x_data,2*x_data+1.0,color='red',linewidth=3)

我们画出这个图想要说明的是，当前选用的数据集点生成模型是可行的，因为点和我们期待生成的那个函数是可以拟合的，大致相似的。

构建模型

模型结构如下：

x=tf.placeholder("float",name="x")
y=tf.placeholder("float",name="y")
# 定义模型函数
def model(x,w,b):return tf.multiply(x,w)+bw=tf.Variable(1.0,name="w0")
b=tf.Variable(0.0,name="b0")
pred=model(x,w,b)#预测值的计算

训练模型

设置训练参数，在这里 learn_rate学习率和迭代次数 train_epochs是超参量参数，也就是我们在训练一个模型的时候必须自己人工定义的参数，通过这种参数去让模型更好的拟合，达到我们希望的效果。我们常说调参调参就是指这个。

#迭代次数
train_epochs=10
#学习率
learn_rate=0.05

定义损失函数

损失函数的作用是指导模型收敛的方向，他表示描述预测值和真实值之间的误差，是一个数。

常见的损失函数有：

• L1损失函数
• l2损失函数
• 均方误差MSE

这里我们使用MSE均方差损失函数。所谓均方差损失函数就是每个点的y值减掉预测的y值在进行平方，然后把这些点的平方都加起来，最后加和结果除以总的点个数。专业的解释是：每个样本的平均平方损失。

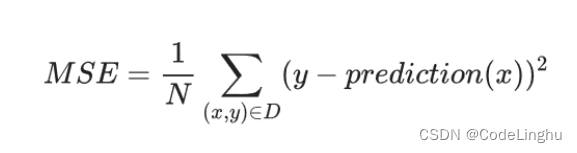
# 采用均方差作为损失函数
loss_function=tf.reduce_mean(tf.square(y-pred))

定义优化器

我们定义优化器的目的是减少模型的损失，使得损失最小化。我们在优化器 Optimzer中会通过 learn_rate学习率和 loss_function损失函数 来优化收敛我们的模型。我们在讨论损失函数的时候，我们希望损失最小，那么我们就要求出损失函数的最小值。怎么求呢？我们需要用到 梯度下降算法。

# 梯度下降优化器
optimizer=tf.train.GradientDescentOptimizer(learn_rate).minimize(loss_function)

如何理解梯度下降呢？首先需要知道这个东西是为了降低损失的，降低损失函数的值！

梯度下降法的基本思想可以类比为一个下山的过程，如下图所示函数看似为一片山林，红色的是山林的高点，蓝色的为山林的低点，蓝色的颜色越深，地理位置越低，则图中有一个低点，一个最低点。

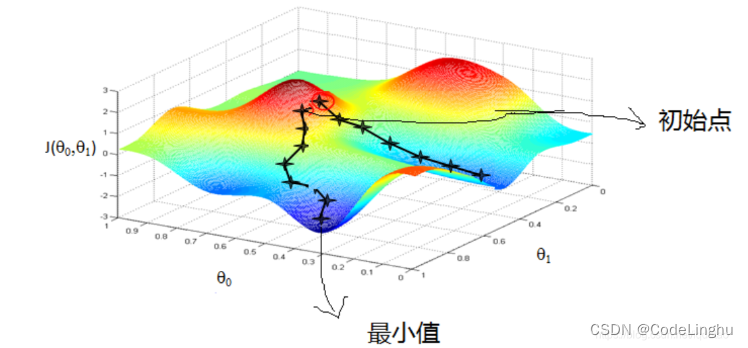
假设这样一个场景：一个人被困在山上（图中红圈的位置），需要从山上下来(找到山的最低点，也就是山谷)，但此时山上的浓雾很大，导致可视度很低。因此，下山的路径就无法确定，他必须利用自己周围的信息去找到下山的路径。这个时候，他就可以利用梯度下降算法来帮助自己下山。具体来说就是，以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着山的高度下降的方向走，然后每走一段距离，都反复采用同一个方法，最后就能成功的抵达山谷。

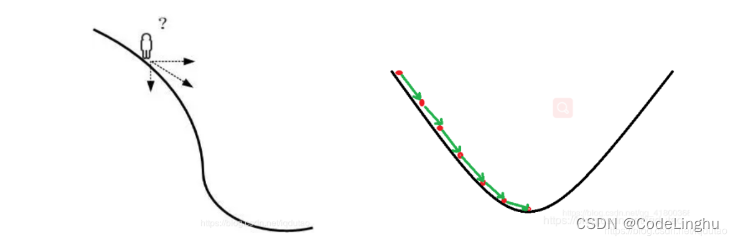
假设这座山最陡峭的地方是无法通过肉眼立马观察出来的，而是需要一个复杂的工具来测量，同时，这个人此时正好拥有测量出最陡峭方向的工具。所以，此人每走一段距离，都需要一段时间来测量所在位置最陡峭的方向，这是比较耗时的。那么为了在太阳下山之前到达山底，就要尽可能的减少测量方向的次数。这是一个两难的选择，如果测量的频繁，可以保证下山的方向是绝对正确的，但又非常耗时，如果测量的过少，又有偏离轨道的风险。所以需要找到一个合适的测量方向的频率（多久测量一次），来确保下山的方向不错误，同时又不至于耗时太多，在算法中我们成为步长。

在这里我们将步长称为 学习率，也就是上面代码中的 learn_rate。学习率不能过大过小，需要我们根据经验设置，过大过小都会导致模型拟合过度。

我们说一个点什么时候梯度最小？也就是说什么时候损失函数最小？

如下图我们对点进行求导，它的导数从数学的角度来说表示斜率，也就是斜线的陡峭程度，这个斜率的值其实就是我们说的梯度。斜线的方向就是我们说的梯度方向。

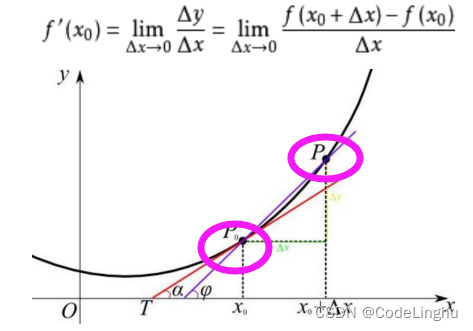
如下图，当点的斜率为0的时候，也就是梯度为0了，这个时候我们说这个模型的损失最小，模型最为拟合。

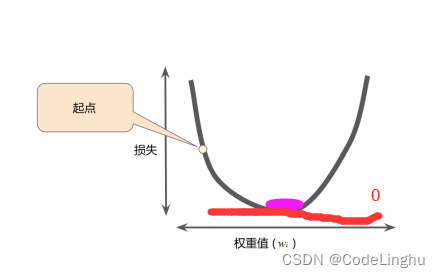
其实我们上面定义的优化器 GradientDescentOptimizer(learn_rate).minimize(loss_function)已经帮我们干了上面所有的事情，它直接通过我们设置好的步长学习率和损失函数，将我们的模型损失降到了最低，也就是上面这张图所需要的效果。

创建会话

sess=tf.Session()
# 所有变量初始化
init=tf.global_variables_initializer()
sess.run(init)

迭代训练

在模型训练阶段，设置多轮迭代，每次通过将样本逐个输入模型，进行梯度下降优化操作，每轮迭代以后，绘制出迭代曲线

# epoch就是训练轮数，这里为10
for epoch in range(train_epochs):for xs,ys in zip(x_data,y_data):_,loss=sess.run([optimizer,loss_function],feed_dict={x:xs,y:ys})#核心b0temp=b.eval(session=sess)w0temp=w.eval(session=sess)plt.plot(x_data,w0temp*x_data+b0temp)

训练结果

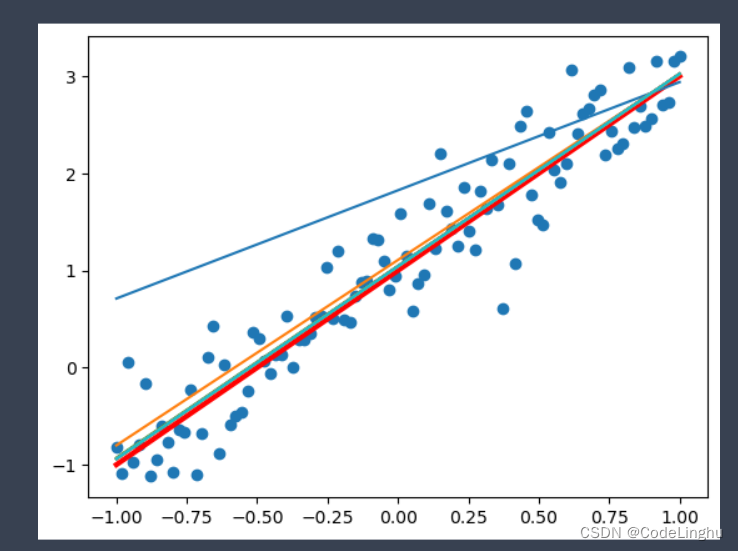
从图中可以得到，这个模型在训练3次以后就接近拟合的状态了。

打印参数和预测值

print("w:",sess.run(w))
print("b:",sess.run(b))
x_test=3.21 #这是预测值
predict=sess.run(pred,feed_dict={x:x_test})
print("预测值：%f" % predict)
target=2*x_test+1.0
print("目标值：%f" % target)

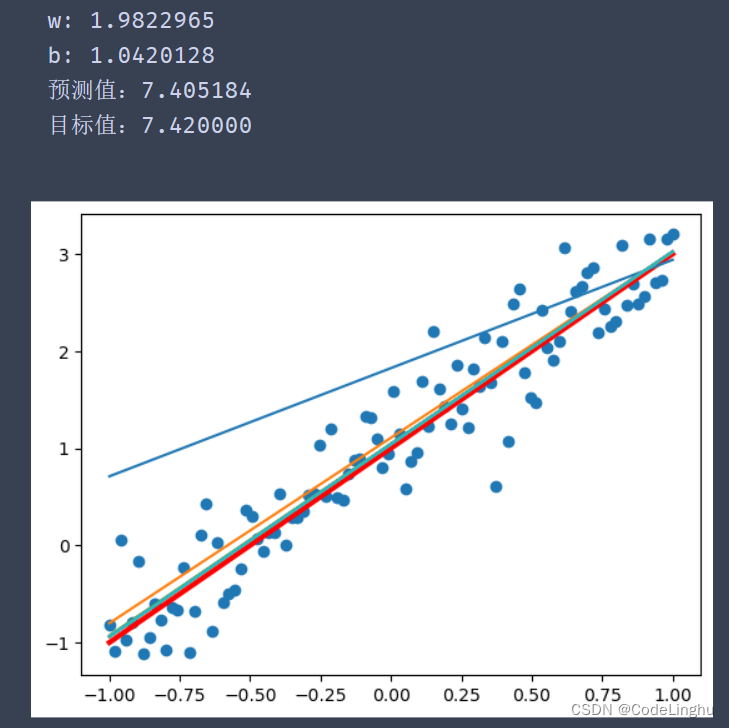
4、完整代码demo

环境：

• Anaconda
• Jupyter
• Python3.5.2
• TensorFlow2.0

%matplotlib inlineimport matplotlib.pyplot as plt
import numpy as np
import tensorflow.compat.v1 as tf
tf.compat.v1.disable_eager_execution()np.random.seed(5)x_data=np.linspace(-1,1,100)
y_data=2*x_data+1.0+np.random.randn(*x_data.shape)*0.4
plt.scatter(x_data,y_data)
plt.plot(x_data,2*x_data+1.0,color='red',linewidth=3)x=tf.placeholder("float",name="x")
y=tf.placeholder("float",name="y")
def model(x,w,b):return tf.multiply(x,w)+bw=tf.Variable(1.0,name="w0")
b=tf.Variable(0.0,name="b0")
pred=model(x,w,b)#设置迭代次数和学习率、损失函数
train_epochs=10
learn_rate=0.05
loss_function=tf.reduce_mean(tf.square(y-pred))optimizer=tf.train.GradientDescentOptimizer(learn_rate).minimize(loss_function)sess=tf.Session()init=tf.global_variables_initializer()sess.run(init)for epoch in range(train_epochs):for xs,ys in zip(x_data,y_data):_,loss=sess.run([optimizer,loss_function],feed_dict={x:xs,y:ys})b0temp=b.eval(session=sess)w0temp=w.eval(session=sess)plt.plot(x_data,w0temp*x_data+b0temp)print("w:",sess.run(w))
print("b:",sess.run(b))x_test=3.21
predict=sess.run(pred,feed_dict={x:x_test})
print("预测值：%f" % predict)target=2*x_test+1.0
print("目标值：%f" % target)

这篇关于深度学习在单线性回归方程中的应用--TensorFlow实战详解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---