概率测度理论方法（第 1 部分）

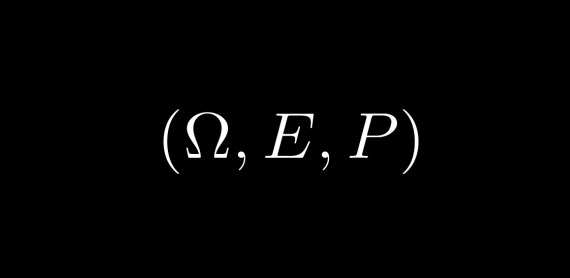
一、说明

        概率的应用范围广泛到经济学、量子力学、生物学甚至政治学，可以说是数学最重要的分支之一。然而，普遍教授和广泛接受的概率版本错过了一些令人难以置信的令人满意的直觉。在本文中，我们将利用这种直觉。为了做到这一点，我们求助于测度理论。对于新手读者来说，测量论，简单来说，就是对尺寸的研究。

在开始之前，定义一些事情很重要。

二、σ-代数

        测度论的核心是 σ 代数的概念。这个概念对于抽象“大小”的概念非常有用。但数学意义上的“大小”是什么意思呢？当然，我们知道大小必须遵循以下直观属性：如果我们将一个物体拆开，那么各个部分的大小之和必须等于该物体本身的大小。

        现在，在我们讨论物体及其部分的大小之前，我们需要一种以数学方式表示这些物体的方法。为了方便起见，我们以集合的形式表示对象。例如，集合 P 可以描述一个粘土球。

        现在，我们需要一种方法来描述如何将对象分解成碎片。这种“将物体分解成碎片”的概念由 P 上的 σ 代数来描述。

σ-代数的正式定义如下：

        给定集合 P 和子集 P' 的集合，如果满足以下条件，则集合 P' 是 P 上的 σ 代数：

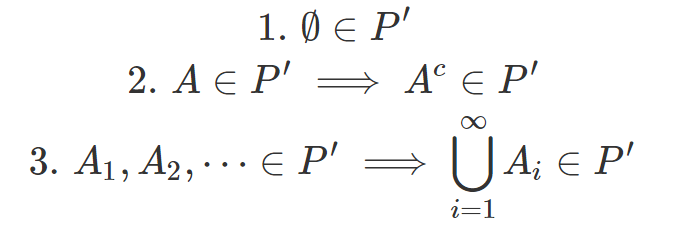
子集集合成为 σ 代数的条件。

        直观上，σ 代数的每个元素代表对象的一个​​“部分”。上面定义中的第一个标准建立了一个“空块”（一块大小为零的块）可以被视为对象的一块。第二个标准确立了这样一个事实：如果我们折断物体的一块 A，那么剩下的物体（A 的补集）也是一个有效的块。最后，第三个标准确立了这样一个事实：如果我们将一组碎片粘合在一起，所得的碎片也是物体的一部分。

        事实上，根据这三个公理，还可以得出σ-代数不仅在集合并集下闭集，而且在集合交集、集合差和对称差下也是闭集的。从数学上来说，这意味着：

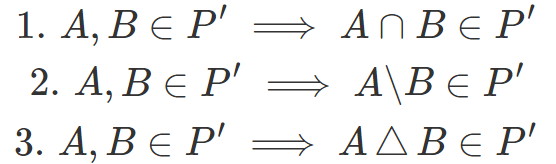
        直观理解 σ-代数的另一种方法是将集合 F 视为破碎的盘子。σ 代数 ℱ 描述了板沿裂纹破裂的所有方式。下图说明了这一点：

在此图像中，F 是物体，ℱ 是 σ 代数。

在该图中，顶部的大椭圆形是一块表面有裂纹的陶瓷板。设板上的点为集合 F。上面，我们说明了每个子集 B ⊆ F ⊆ ℱ。您可以将每个 B 视为代表去除了块的某种组合的盘子。只有当一块周围有裂缝时，我们才可以移除它。我们移除盘子大块的方法的整套配置是 F 上的 σ 代数 ℱ。

三、测量空间

        既然我们已经满足了分解物体的直观属性，我们就可以量化“大小”了。为此，我们转向测量空间。我们首先按以下方式定义一个度量：

        给定集合 P 和 P 上的 σ 代数（表示为 P'），函数

        是满足以下公理时的度量：

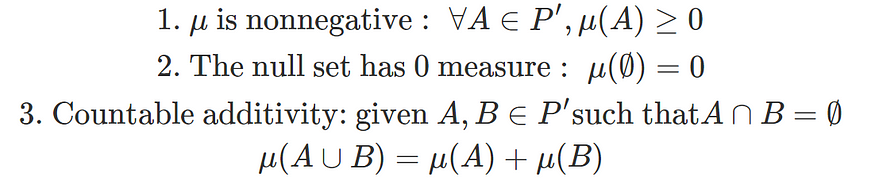
        在这里，度量与尺寸同义。因此，第一个标准本质上是说衡量标准不能为负。第二个标准说，没有任何东西的度量是 0。最后，两个不同部分的度量只是它们的度量之和。

        我们可以通过扩展上面陶瓷板的例子来说明这一点。这里，F 是对象，ℱ 是 F 上的 σ 代数。

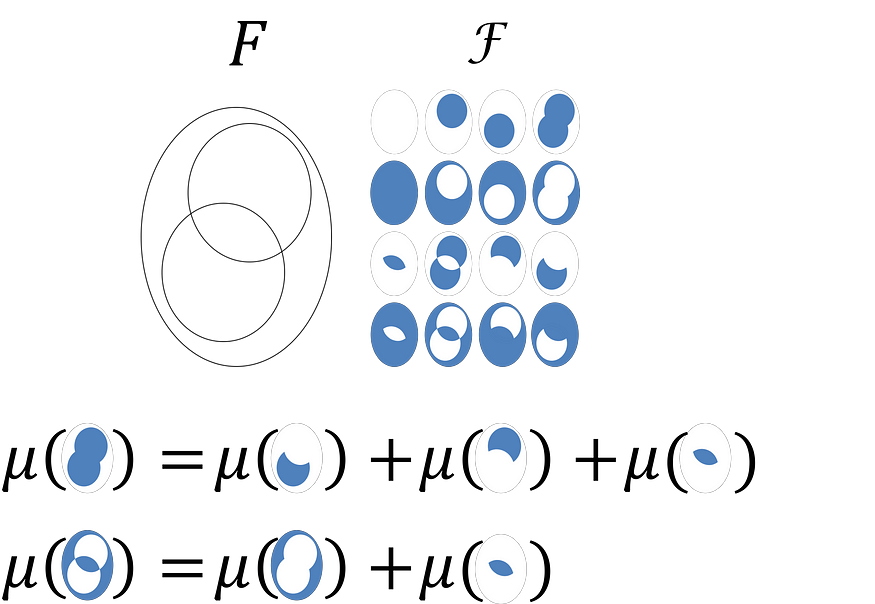
        现在，我们结合所涵盖的所有内容来定义一个新想法：测量空间。测度空间只是集合（对象）、σ 代数（对象的部分）和测度（对象部分的“大小”）的组合。接下来是严格的定义。

        最后，我们定义一个可测量空间如下：

        可测空间是由集合和 σ 代数组成的对。可测量空间中的“可测量”一词暗指它能够配备测量装置。一旦配备了量具，就形成了一个完整的量具空间。

四、概率空间

        这与概率有何关系？好吧，我们可以将测度空间的定义调整为概率空间。概率空间定义如下：

        在理解了测度论的基础知识之后，我们对概率的新定义似乎有了一种更加直观的定义方式。集合 Ω 是样本空间，或所有可能结果的集合。Ω 上的 σ 代数是将所有可能结果划分为事件的一种方法，这是一个熟悉的概念。概率测度 P 只是为事件发生的概率赋值的一种方式——另一个熟悉的概念。并且，由于样本空间中的某些事件肯定会发生，因此 P(Ω)=1。

        至此，我们为更先进的概率概念发展为测度理论概念奠定了基础。在第二部分中，我们将深入研究离散和连续概率分布以及如何使用测度论来统一这两个概念。