左神算法基础class3—题目11判断一个链表是否为回文结构（不同额外空间复杂度的三种方法）

2023-12-07 19:18
文章标签 算法 基础 链表 方法 题目 三种 判断 是否 复杂度 空间 不同 额外 左神 回文结构 class3

本文主要是介绍左神算法基础class3—题目11判断一个链表是否为回文结构（不同额外空间复杂度的三种方法），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

左神算法基础class3—题目11三种方法判断一个链表是否为回文结构

  • 题目：判断一个链表是否为回文结构
  • 方法一：利用堆栈结构(额外空间复杂度O(n))
    • （1）分析
    • （2）核心代码
      • ①头节点初始化
      • ②初始化链表数据
      • ③比较栈和链表是否相同
    • （3）完整代码
  • 方法二：利用快慢指针和堆栈结构（额外空间复杂度O(n/2)）
    • （1）分析
    • （2）核心代码
      • 快慢指针
    • （3）完整代码
  • 方法三：利用快慢指针和逆序一半链表（额外空间复杂度O(1)）
    • （1）分析
    • （2）核心代码
      • ①从头开始的快慢指针
      • ②逆序过程
      • ③比较链表首尾端是否相同
      • ④重排链表恢复如前
    • （3）完整代码

题目：判断一个链表是否为回文结构

【题目】 给定一个链表的头节点head，请判断该链表是否为回文结构。 例如： 1->2->1，返回true。 1->2->2->1，返回true。15->6->15，返回true。 1->2->3，返回false。

进阶： 如果链表长度为N，时间复杂度达到O(N)，额外空间复杂度达到O(1)。

理解：回文结构指中间有对称轴两侧是逆序关系或者是从正方向、反方向遍历值都相同

方法一：利用堆栈结构(额外空间复杂度O(n))

思路：从正方向、反方向遍历值都相同

（1）分析

将链表按顺序存入堆栈结构中，那么栈的弹出顺序与链表的顺序刚好相反。对比栈顶元素与链表当前元素，如果不同返回false，如果相同弹出栈并把链表指向下一元素，不断遍历至空，若全部相同返回true。

（2）核心代码

①头节点初始化

注意：头节点需指向空

List MakeEmpty()
{List head = (List)malloc(sizeof(listnode));head->next = NULL;return head;
}

②初始化链表数据

使用尾插法，r是指向尾部的指针，找到链表末尾并加入新节点

List insert(List head,int num)
{//初始化新节点List p = (List)malloc(sizeof(listnode));p->val = num;p->next = NULL;//找到链表末尾List r = head;while(r->next != NULL){r = r->next; }//将新节点加入链表r->next = p;return head;
}

③比较栈和链表是否相同

将链表内容入栈，比较栈与链表的内容

bool IsPalindromeList(List head)
{List cur = head->next;//保留头节点stack<int> s1,s2,s_cur;//把链表的内容入栈while(cur!= NULL)	{s1.push(cur->val);cur = cur->next;}//比较链表和栈的内容while(!s1.empty()) 	{if(s1.top() == head->next->val)//头节点的下一个节点是链表的第一个有效节点{s1.pop();head = head->next;}elsereturn false;}return true;
}

（3）完整代码

#include<iostream>
#include<stack>using namespace std;
typedef struct listnode
{int val ;listnode *next;
}*List;bool IsPalindromeList(List head)
{List cur = head->next;//保留头节点stack<int> s1,s2,s_cur;while(cur!= NULL) //把链表的内容入栈{s1.push(cur->val);cur = cur->next;}while(!s1.empty()) //比较链表和栈的内容{if(s1.top() == head->next->val){s1.pop();head = head->next;}elsereturn false;}return true;
}List insert(List head,int num)
{//初始化新节点List p = (List)malloc(sizeof(listnode));p->val = num;p->next = NULL;//找到链表末尾List r = head;while(r->next != NULL){r = r->next; }//将新节点加入链表r->next = p;return head;
}List MakeEmpty()
{List head = (List)malloc(sizeof(listnode));head->next = NULL;return head;
}int main()
{List head = MakeEmpty();insert(head,8);insert(head,10);insert(head,7);insert(head,10);insert(head,8);cout<<IsPalindromeList(head);system("pause");return 0;
}

方法二：利用快慢指针和堆栈结构（额外空间复杂度O(n/2)）

思路：若是回文结构，从后半部分与前半部分刚好相反。

（1）分析

使用快慢指针，快指针一次走两步，慢指针一次走一步。当快指针走完时慢指针走到一半。将慢指针的后一半入堆栈，出栈时(相当于后半部分逆序)元素如果和链表前半部分相同则是回文结构。与方法一相比，由于堆栈只存放一半元素，所以额外空间复杂度减半为n/2。
本方法的难点在于不论奇偶情况恰好让慢指针停在中间后一个的位置。
情况一：一共偶数个数
①刚开始慢指针指向第二个数，快指针指向第一个数；

在这里插入图片描述
②快指针走两步，慢指针走一步

在这里插入图片描述

③快指针走两步，慢指针走一步
在这里插入图片描述
④不能继续了，把慢指针指向的数依次入栈（7,10,8），再进行比较

情况二：一共奇数个数

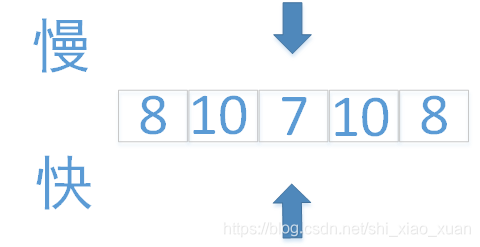
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
和情况一相同，最后把10,8入栈再比较。

（2）核心代码

快慢指针

如果链表为空或者只有一个元素返回true，慢指针指向第二个数，快指针指向第一个数。在快指针能走的情况下，快指针一次走两步，慢指针一次走一步。

head = head->next;if (head == NULL|| head->next == NULL) return true;List p1,p2;p2 = head;		//快指针p1 = head->next;//慢指针while(p2->next != NULL && p2->next->next != NULL){p2 = p2->next->next;p1 = p1->next;}

②比较代码和方法一相同，代码复用

（3）完整代码

//使用快慢指针判断是否是回文链表
#include<iostream>
#include<stack>using namespace std;
typedef struct listnode
{int val ;listnode *next;
}*List;bool IsPalindromeList(List head)
{head = head->next;if (head == NULL|| head->next == NULL) return true;List p1,p2;p2 = head;		//快指针p1 = head->next;//慢指针while(p2->next != NULL && p2->next->next != NULL){p2 = p2->next->next;p1 = p1->next;}//链表入栈stack<int> s1;while(p1!=NULL){s1.push(p1->val);p1 = p1->next ;}//对比while(!s1.empty()){if(head->val == s1.top()){s1.pop();head = head->next;}elsereturn false;}return true;
}List insert(List head,int num)
{//初始化新节点List p = (List)malloc(sizeof(listnode));p->val = num;p->next = NULL;//找到链表末尾List r = head;while(r->next != NULL){r = r->next; }//将新节点加入链表r->next = p;return head;
}List MakeEmpty()
{List head = (List)malloc(sizeof(listnode));head->next = NULL;return head;
}int main()
{List head = MakeEmpty();insert(head,8);insert(head,10);insert(head,7);insert(head,7);insert(head,10);insert(head,8);cout<<IsPalindromeList(head);system("pause");return 0;
}

方法三：利用快慢指针和逆序一半链表（额外空间复杂度O(1)）

Tips方法三实现起来比方法一、方法二复杂很多，一般只在面试过程中追求最小额外空间复杂度时使用。笔试追求稳，快用方法一和方法二。
思路：若是回文结构，后半部分逆序后与前半部分刚好相同。

（1）分析

总体分为四步，首先找到中间值，再逆序后半部分，接着进行比较，最后重排恢复链表，具体如下。
使用快慢指针，快指针一次走两步，慢指针一次走一步。当快指针走完时慢指针走到一半。方法二链表为奇数项时慢指针停在中间靠右一个位置，而方法三慢指针在正中间。从中间项开始逆序，不用辅助空间（参考反转单向和双向链表）。逆序过后，对比链表从后向前的数据和从前向后的顺序。最后，由于没有用辅助空间，链表的顺序发生了变化，需要重排链表变回原来的链表，依旧是一个逆序的过程。

本方法的难点依旧在于不论奇偶情况，奇数项停在中间，偶数项停在中间后一个位置。
与方法二不同，快慢指针最开始都在第一个数，对于奇数项的链表慢指针刚好走到中间位置，而对于偶数项的链表，先让快慢指针各走一步，之后如果快指针不能走了就结束。这样在奇数情况下快、慢指针至少走一步，只剩一个数时，慢指针依旧可以走一步，就比方法二一次走两步的情况多走了一步，慢指针最终停在中间后一个数。
情况一：一共奇数个数
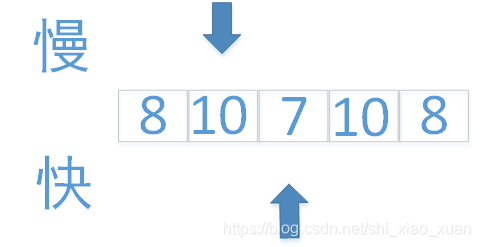
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
情况二：一共偶数个数

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
上图时快指针没有到最后，快慢指针都可以继续走一步，走到下图时快指针达到最后，结束
在这里插入图片描述

（2）核心代码

①从头开始的快慢指针

原理如上图所示，先让快慢指针走一步再继续判断快指针是否走到最后。此处的while循环条件是快指针能不能走一步，而不是快指针能不能走两步。记录p1_pre的位置，也就是不逆序的最后一个数，最后重排时碰到p1_pre 停止。

	p2 = head;//快指针p1 = head;//慢指针while(p2->next != NULL){p1_pre = p1;p2 = p2->next;p1 = p1->next;if(p2->next == NULL){break;}p2 = p2->next;

②逆序过程

p1是中间节点的位置，从中间节点开始逆序，需要暂存当前节点、前一节点和下一节点。参考反转单向和双向链表

	List cur = p1;List pre = NULL;while(cur!=NULL){List temp = cur->next;cur->next = pre;pre = cur;cur = temp;}

③比较链表首尾端是否相同

依次比较链表头端和尾端的数，如果有一位不相同res是false,退出比较，但是不能立刻返回，因为还需要重排链表，逆序过后pre是保留的最后一个数需要记录下来，重排时的开始条件就是pre

	//比较bool res = true;cur = pre;	//逆序过后pre是保留的最后一个数while(cur != NULL){if(cur->val != head->val){res = false;break;}cur = cur->next;head = head->next;}

④重排链表恢复如前

由逆序的最后一个数pre开始,终止条件是cur不为空且碰到未逆序的最后一个数为止

	//重排cur = pre;pre = NULL;while(cur!=NULL && cur!= p1_pre){List temp = cur->next;cur->next = pre;pre = cur;cur = temp;}

（3）完整代码

//使用快慢指针但不用辅助空间判断是否是回文链表
#include<iostream>using namespace std;
typedef struct listnode
{int val ;listnode *next;
}*List;bool IsPalindromeList(List head)
{head = head->next;if (head == NULL|| head->next == NULL) return true;List p1,p2,p1_pre = NULL;p2 = head;//快指针p1 = head;//慢指针while(p2->next != NULL){p1_pre = p1;p2 = p2->next;p1 = p1->next;if(p2->next == NULL){break;}p2 = p2->next;}//逆序List cur = p1;List pre = NULL;while(cur!=NULL){List temp = cur->next;cur->next = pre;pre = cur;cur = temp;}//比较bool res = true;cur = pre;//pre是保留的最后一个数while(cur != NULL){if(cur->val != head->val){res = false;break;}cur = cur->next;head = head->next;}//重排cur = pre;pre = NULL;while(cur!=NULL && cur!= p1_pre){List temp = cur->next;cur->next = pre;pre = cur;cur = temp;}return res;
}List insert(List head,int num)
{//初始化新节点List p = (List)malloc(sizeof(listnode));p->val = num;p->next = NULL;//找到链表末尾List r = head;while(r->next != NULL){r = r->next; }//将新节点加入链表r->next = p;return head;
}List MakeEmpty()
{List head = (List)malloc(sizeof(listnode));head->next = NULL;return head;
}int main()
{List head = MakeEmpty();insert(head,1);insert(head,2);insert(head,3);insert(head,4);insert(head,4);insert(head,3);insert(head,2);insert(head,0);cout<<IsPalindromeList(head);system("pause");return 0;
}

这篇关于左神算法基础class3—题目11判断一个链表是否为回文结构（不同额外空间复杂度的三种方法）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/467053。

相关文章

Java中Arrays类和Collections类常用方法示例详解

Java中Arrays类和Collections类常用方法示例详解

《Java中Arrays类和Collections类常用方法示例详解》本文总结了Java中Arrays和Collections类的常用方法,涵盖数组填充、排序、搜索、复制、列表转换等操作,帮助开发者高... 目录Arrays.fill()相关用法Arrays.toString()Arrays.sort()A
阅读更多...
Nginx安全防护的多种方法

Nginx安全防护的多种方法

《Nginx安全防护的多种方法》在生产环境中,需要隐藏Nginx的版本号,以避免泄漏Nginx的版本,使攻击者不能针对特定版本进行攻击,下面就来介绍一下Nginx安全防护的方法,感兴趣的可以了解一下... 目录核心安全配置1.编译安装 Nginx2.隐藏版本号3.限制危险请求方法4.请求限制（CC攻击防御）
阅读更多...
python生成随机唯一id的几种实现方法

python生成随机唯一id的几种实现方法

《python生成随机唯一id的几种实现方法》在Python中生成随机唯一ID有多种方法,根据不同的需求场景可以选择最适合的方案,文中通过示例代码介绍的非常详细,需要的朋友们下面随着小编来一起学习学习... 目录方法 1：使用 UUID 模块（推荐）方法 2：使用 Secrets 模块（安全敏感场景）方法
阅读更多...
MyBatis-Plus通用中等、大量数据分批查询和处理方法

MyBatis-Plus通用中等、大量数据分批查询和处理方法

《MyBatis-Plus通用中等、大量数据分批查询和处理方法》文章介绍MyBatis-Plus分页查询处理,通过函数式接口与Lambda表达式实现通用逻辑,方法抽象但功能强大,建议扩展分批处理及流式... 目录函数式接口获取分页数据接口数据处理接口通用逻辑工具类使用方法简单查询自定义查询方法总结函数式接口
阅读更多...
MySQL深分页进行性能优化的常见方法

MySQL深分页进行性能优化的常见方法

《MySQL深分页进行性能优化的常见方法》在Web应用中,分页查询是数据库操作中的常见需求,然而,在面对大型数据集时,深分页（deeppagination）却成为了性能优化的一个挑战,在本文中,我们将... 目录引言：深分页，真的只是“翻页慢”那么简单吗？一、背景介绍二、深分页的性能问题三、业务场景分析四、
阅读更多...
JAVA中安装多个JDK的方法

JAVA中安装多个JDK的方法

《JAVA中安装多个JDK的方法》文章介绍了在Windows系统上安装多个JDK版本的方法,包括下载、安装路径修改、环境变量配置（JAVA_HOME和Path）,并说明如何通过调整JAVA_HOME在... 首先去oracle官网下载好两个版本不同的jdk（需要登录Oracle账号，没有可以免费注册）下载完
阅读更多...
Java中读取YAML文件配置信息常见问题及解决方法

Java中读取YAML文件配置信息常见问题及解决方法

《Java中读取YAML文件配置信息常见问题及解决方法》：本文主要介绍Java中读取YAML文件配置信息常见问题及解决方法,本文给大家介绍的非常详细,对大家的学习或工作具有一定的参考借鉴价值,需要... 目录1 使用Spring Boot的@ConfigurationProperties2. 使用@Valu
阅读更多...
Java 方法重载Overload常见误区及注意事项

Java 方法重载Overload常见误区及注意事项

《Java方法重载Overload常见误区及注意事项》Java方法重载允许同一类中同名方法通过参数类型、数量、顺序差异实现功能扩展,提升代码灵活性,核心条件为参数列表不同,不涉及返回类型、访问修饰符... 目录Java 方法重载（Overload）详解一、方法重载的核心条件二、构成方法重载的具体情况三、不构
阅读更多...
SQL中如何添加数据(常见方法及示例)

SQL中如何添加数据(常见方法及示例)

《SQL中如何添加数据(常见方法及示例)》SQL全称为StructuredQueryLanguage,是一种用于管理关系数据库的标准编程语言,下面给大家介绍SQL中如何添加数据,感兴趣的朋友一起看看吧... 目录在mysql中，有多种方法可以添加数据。以下是一些常见的方法及其示例。1. 使用INSERT I
阅读更多...
Ubuntu如何分配​​未使用的空间

Ubuntu如何分配​​未使用的空间

《Ubuntu如何分配​​未使用的空间》Ubuntu磁盘空间不足,实际未分配空间8.2G因LVM卷组名称格式差异（双破折号误写）导致无法扩展,确认正确卷组名后,使用lvextend和resize2fs... 目录1：原因2：操作3：报错5：解决问题：确认卷组名称​6：再次操作7：验证扩展是否成功8：问题已解
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2