左神算法基础class3—题目6旋转正方形矩阵

本文主要是介绍左神算法基础class3—题目6旋转正方形矩阵，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.题目

【题目】 给定一个整型正方形矩阵matrix，请把该矩阵调整成
顺时针旋转90度的样子。
【要求】 额外空间复杂度为O(1)，不使用辅助数组。

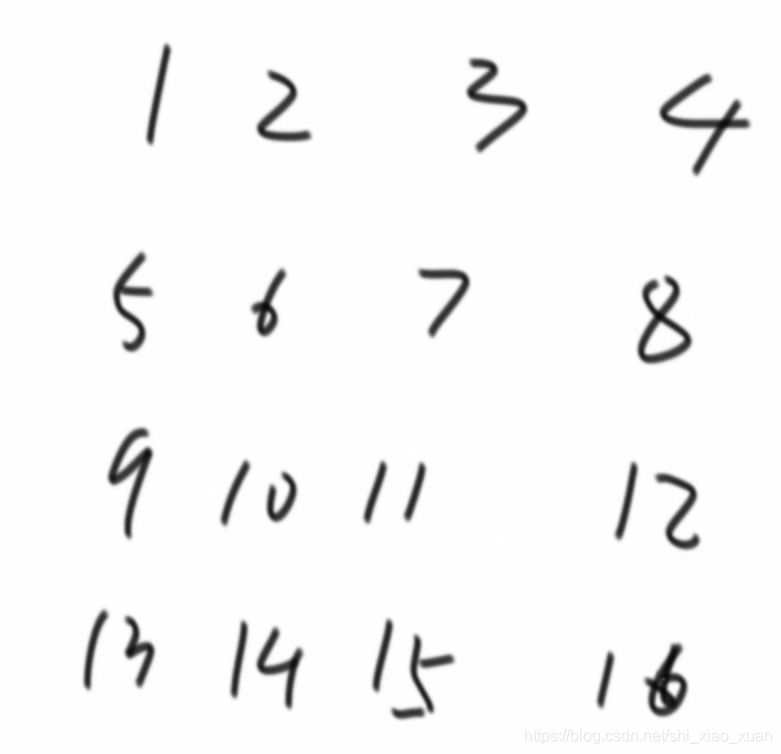
2.分析

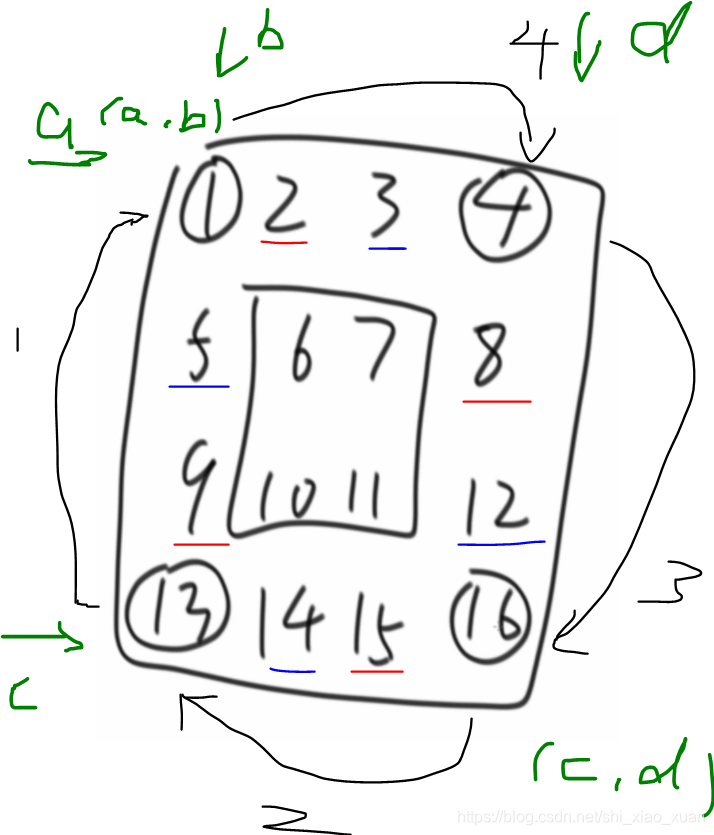
分析：题目给定的是正方形矩阵，考虑把矩阵看成回字形结构，由外到内按层进行旋转，先外层后内层。与题目5思路相同规定左上角和右下角的点为（a,b）（c,d）。由于不能使用辅助数组，旋转会覆盖之前的数所以需要一个temp变量暂存某个数。
（1）暂存数字1后通过a,b,c,d四个变量对1,4,16,13四个数按照黑色箭头的顺序逐个覆盖掉之前的数；
（2）对a行上的方向依次把2,8,15,9与（1）步骤相似的旋转覆盖，3,12,14,5也是如此，这样最外层的12个数旋转完成；
（3）a++,b++,c–,d–后对内层6,7,11,10相同操作。
tips：最外层每行4个数，有三个起始点1,2,3，内层每行2两个数只有一个起始点6，那么d-b表示需要的起始点个数即每层需要循环多少次。本题外层循环三次可以旋转12个数，内层四个数循环一次。

3.核心代码

（1）初始化a,b,c,d。

int a = 0,b = 0,c = height - 1,d = width - 1;

（2）每层旋转的代码，通过i和a,b,c,d控制数组的位置,单纯考察代码能力

void rotate_matrix(int arr[][width],int a,int b,int c,int d)
{int times = d - b;for(int i = 0;i < times;i++){int temp = arr[a][b + i];arr[a][b + i] = arr[c - i][b];arr[c - i][b] = arr[c][d - i];arr[c][d - i] = arr[a + i][d];arr[a + i][d] = temp;}
}

（3）通过a,c两个变量控制一共需要旋转的层数。左上角和右下角的点每层旋转过后逐渐向中心移动一格，由于题目给定是正方形，那么两个点只能重合不可能斜错，使用两个点的横坐标a,c控制旋转层数。

while(a < c){rotate_matrix(arr,a++,b++,c--,d--);}

4.完整代码

#include<iostream>
#define height 4
#define width 4
using namespace std;void rotate_matrix(int arr[][width],int a,int b,int c,int d)
{int times = d - b;for(int i = 0;i < times;i++){int temp = arr[a][b + i];arr[a][b + i] = arr[c - i][b];arr[c - i][b] = arr[c][d - i];arr[c][d - i] = arr[a + i][d];arr[a + i][d] = temp;}
}void print(int arr[][width])
{//打印输出for(int i = 0;i < height;i++){for(int j = 0;j < width;j++){cout<<arr[i][j]<<" " ;}cout<<endl;}
}
int main()
{//int arr[height][width] = {1,2,3,4,5,6,7,8,9};int arr[height][width] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};int a = 0,b = 0,c = height - 1,d = width - 1;while(a < c){rotate_matrix(arr,a++,b++,c--,d--);}print(arr);system("pause");return 0;
}

5.输出结果

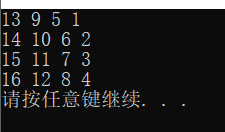
这篇关于左神算法基础class3—题目6旋转正方形矩阵的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---