左神算法基础class3—题目5转圈打印矩阵

本文主要是介绍左神算法基础class3—题目5转圈打印矩阵，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.题目

给定一个整型矩阵matrix，请按照转圈的方式打印它。
例如： 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 打印结果为：1，2，3，4，8，12，16，15，14，13，9，5，6，7，11， 10
【要求】 额外空间复杂度为O(1)。

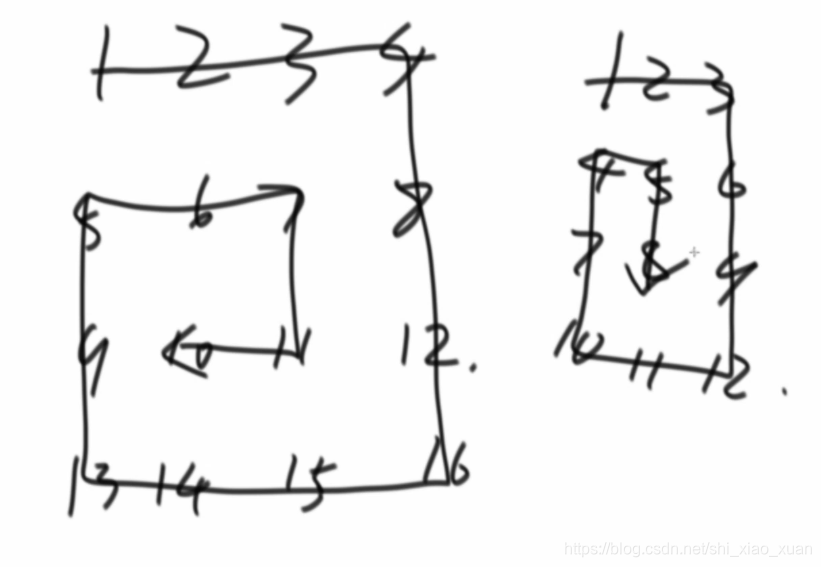
2.分析

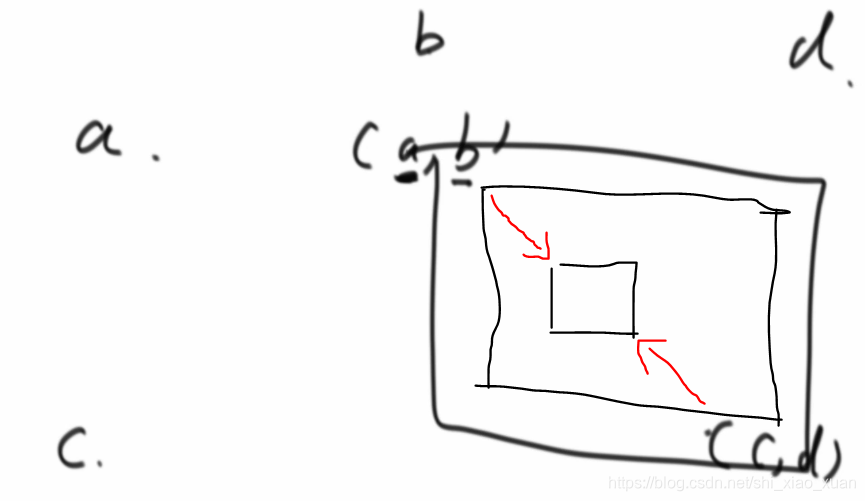
（1）本题考虑使用a,b,c,d四个变量控制边界，如下图所示a，c表示行，b，d表示列（a,b）是左上角点，(c,d)是右下角点。按照题目要求打印a橫行，d纵行，c逆序橫行，b逆序纵行。之后a++，b++，c–，d–，也就是把左上角的点向右下角移动，把右下角的点往左上角移动。继续打印里面的方形框，再更改a,b,c,d的值直到 （a,b）,(c,d)重合或者相错结束。

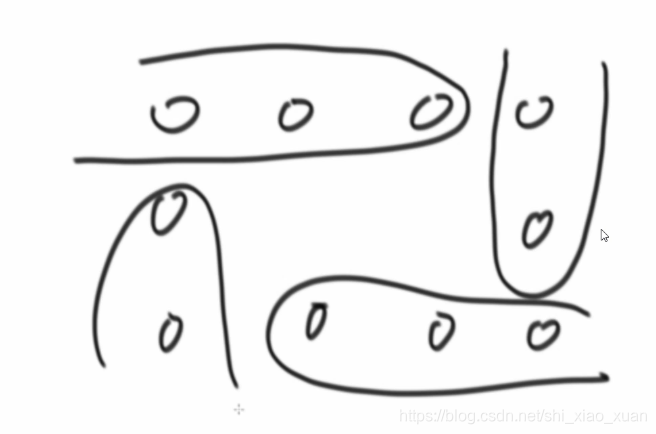
（2）为了打印方便，考虑下图方式打印，拐点用于下一组开头不打印，打印其余的数。

3.核心代码

（2）打印到最后一组形成单独的行和列如题图，并不能构成方形框进行打印，故需要先进行判别，条件是ac和bd。

void print_num(int arr[][height],int a,int b,int c,int d)
{if(a==c){for(int i = b;i <= d;i++){cout<<arr[a][i]<<" ";}}else if(b==d){for(int i = a;i <= c;i++){cout<<arr[i][b]<<" ";}}else{int cur_i = a;int cur_j = b;while(cur_j != d){cout<<arr[a][cur_j]<<" ";cur_j++;}while(cur_i != c){cout<<arr[cur_i][d]<<" ";cur_i++;}while(cur_j != b){cout<<arr[c][cur_j]<<" ";cur_j--;}while(cur_i != a){cout<<arr[cur_i][b]<<" ";cur_i--;}}
}

（2）调用打印的条件是左上角的点不能与右下角的点相错，加上等于号是指当他们重合时剩下最后一个数也必须打印

while(a <= c && b <= d){print_num(arr,a,b,c,d);a++,b++,c--,d--;}

4.完整代码

#include<iostream>
#define height 3
#define width 3
using namespace std;void print_num(int arr[][height],int a,int b,int c,int d)
{if(a==c){for(int i = b;i <= d;i++){cout<<arr[a][i]<<" ";}}else if(b==d){for(int i = a;i <= c;i++){cout<<arr[i][b]<<" ";}}else{int cur_i = a;int cur_j = b;while(cur_j != d){cout<<arr[a][cur_j]<<" ";cur_j++;}while(cur_i != c){cout<<arr[cur_i][d]<<" ";cur_i++;}while(cur_j != b){cout<<arr[c][cur_j]<<" ";cur_j--;}while(cur_i != a){cout<<arr[cur_i][b]<<" ";cur_i--;}}
}
int main()
{int arr[height][width] = {1,2,3,4,5,6,7,8,9};//int arr[height][width] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};int a = 0,b = 0,c = height - 1,d = width - 1;while(a <= c && b <= d){print_num(arr,a,b,c,d);a++,b++,c--,d--;}system("pause");return 0;
}

5.输出结果

这篇关于左神算法基础class3—题目5转圈打印矩阵的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---