本文主要是介绍台湾国立大学郭彦甫Matlab教程笔记(15)polynomial integration 多项式积分,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
台湾国立大学郭彦甫Matlab教程笔记(15)
Polynomial integration多项式积分
一个多项式和它的积分如下

MATlAB中如何计算积分?
polynomial integration :polyint()
多项式积分的函数:polyint()
这个函数怎样用呢?
polyint(p,3),其中第一个参数是被积多项式的系数向量,第二个参数是给定的常数。
举例:计算下面函数的积分,取常数为3,并且计算派生的,在7这一点的积分值

根据数学知识,我们知道这个函数的积分出来是不定积分,如下,需要指定这个常数k,这里是k=3
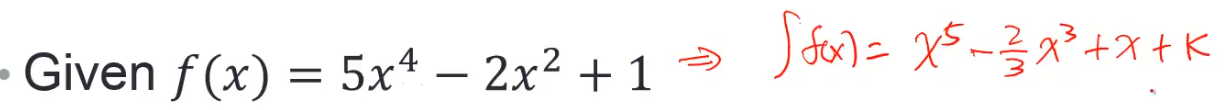
例程:
p=[5,0,-2,0,1];
polyint(p,3);%第二个参数是需要添加的常数
这个时候问你在x=7的时候积分数值是多少,就要使用polyval()这个函数指令
polyval(polyint(p,3),7);
运行的结果:可以看出的确计算出来积分的结果

而且在x=7处这个积分函数的值是

学到这里,需要对知识点进行练习:
下面是自己对自己的练习:请绘制出来上述积分曲线的图形
我的代码:
p=[5,0,-2,0,1];%被积函数的系数
%常数是3的积分函数
A=polyint(p,3);%得到的是系数
%现在需要得到积分的值
x=-2:0.01:2;%自变量范围
f=polyval(A,x);%积分函数的y值
plot(x,f);
xlabel('x');ylabel('∫f(x)');运行结果:

【总结】
多项式积分用到的函数时polyint,这个函数名时polynomial integration(多项式积分)的缩写,这样容易记住,得到的结果类似于多项式微分,得到的是一个系数向量。
计算积分的值仍然需要polyval()这个函数。
给出一个绘制积分函数曲线的例程。
这篇关于台湾国立大学郭彦甫Matlab教程笔记(15)polynomial integration 多项式积分的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







