polynomial专题
Quotient Polynomial
第一次的时候理解错题意了,以为是输入与K有关。。。我也不知道我怎么想的。。。反正后来改对啦 Problem B Quotient Polynomial Time Limit 2 Seconds A polynomial of degree n can be expressed as If k is any integer then we can write:
Spark MLlib 特征工程系列—特征转换Polynomial Expansion
Spark MLlib 特征工程系列—特征转换Polynomial Expansion 1. Polynomial Expansion 简介 PolynomialExpansion 是 Spark MLlib 中的一种特征转换工具,主要用于将原始特征进行多项式扩展。多项式扩展通过生成原始特征的所有多项式组合来增加特征的维度,从而提高模型的表达能力。这种方法在非线性问题的建模中非常有用,因为它允
1204 ACdream Integration of Polynomial(数学:简单求积分)
很容易的一个题,但是题目有个坑 比如说输入: 1 -1 1 输出结果应该为:-1/2 2 而不是:1/-2 2 但是题目中又没有说清楚 感觉是因为题目不严谨 代码如下: #include <cstdio>#include <cstring>#include <iostream>#include <algorithm>#define MAXN 1010#define
polynomial regression
在上一节所介绍的非线性回归分析,首先要求我们对回归方程的函数模型做出判断。虽然在一些特定的情况下我们可以比较容易地做到这一点,但是在许多实际问题上常常会令我们不知所措。根据高等数学知识我们知道,任何曲线可以近似地用多项式表示,所以在这种情况下我们可以用多项式进行逼近,即多项式回归分析。 一、多项式回归方法 假设变量y与x的关系为p次多项式,且在xi处对y的随机误差 (i=1,2,…,
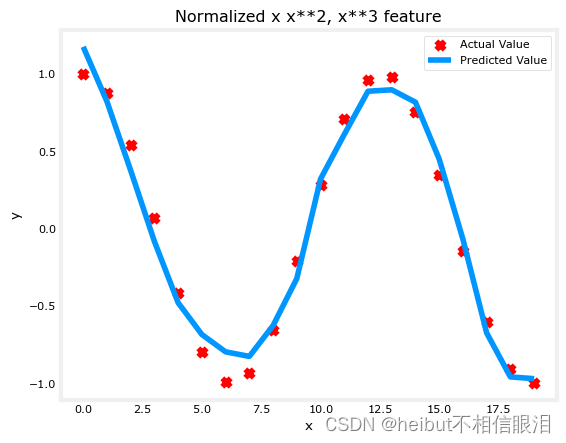
吴恩达机器学习-可选实验室:特征工程和多项式回归(Feature Engineering and Polynomial Regression)
文章目录 目标工具特征工程和多项式回归概述多项式特征选择功能备用视图扩展功能复杂的功能 恭喜! 目标 在本实验中,你将:探索特征工程和多项式回归,它们允许您使用线性回归的机制来拟合非常复杂,甚至非常非线性的函数。 工具 您将利用在以前的实验中开发的函数以及matplotlib和NumPy。 import numpy as npimport matplotlib.pypl
【DataStructure】Another usage of List: Polynomial
Statements: This blog was written by me, but most of content is quoted from book【Data Structure with Java Hubbard】 【Description】 Apolynomialis a mathematical function of the form:
线性回归(linear_regression),多项式回归(polynomial regression)(Tensorflow实现)
#回归import numpy as npimport tensorflow as tfimport matplotlib.pyplot as pltn_observations=100xs=np.linspace(-3,3,n_observations)ys=np.sin(xs)+np.random.uniform(-0.5,0.5,n_observations)plt.scatt
1.1介绍与多项式曲线拟合(Polynomial Curve Fitting)
今天开始学Pattern Recognition and Machine Learning (PRML),章节1.1,介绍与多项式曲线拟合(Polynomial Curve Fitting) 转载请注明源地址:http://www.cnblogs.com/xbinworld/archive/2013/04/21/3034300.html Pattern Recognition
abc D - Polynomial division
传送门:D - Polynomial division 题目大意:给出A(x)和C(x)多项式的序数,A(x)*B(x) = C(x),求B(x)。 坑:这题不能够顺着想,那样会很复杂,但是一旦把数组倒过来,先求B(m),题意就会明朗很多了。 #include <bits/stdc++.h>using namespace std;int main() {int N, M;cin >> N >
PCL-表面(Surface)Smoothing and normal estimation based on polynomial reconstruction
Moving Least Squares(MLS) 移动最小二乘法,可以用来平滑和重采样,接下来将介绍使用方法。https://en.wikipedia.org/wiki/Moving_least_squares(MLS介绍) 使用统计分析很难去除一些数据不规则(由小距离测量误差引起)。 要创建完整的模型,必须考虑光泽表面以及数据中的遮挡。 在无法获得额外扫描的情况下,解决方案是使用重采样算法,
台湾国立大学郭彦甫Matlab教程笔记(15)polynomial integration 多项式积分
台湾国立大学郭彦甫Matlab教程笔记(15) Polynomial integration多项式积分 一个多项式和它的积分如下 MATlAB中如何计算积分? polynomial integration :polyint() 多项式积分的函数:polyint() 这个函数怎样用呢? polyint(p,3),其中第一个参数是被积多项式的系数向量,第二个参数是给定的常数。 举例:计算下
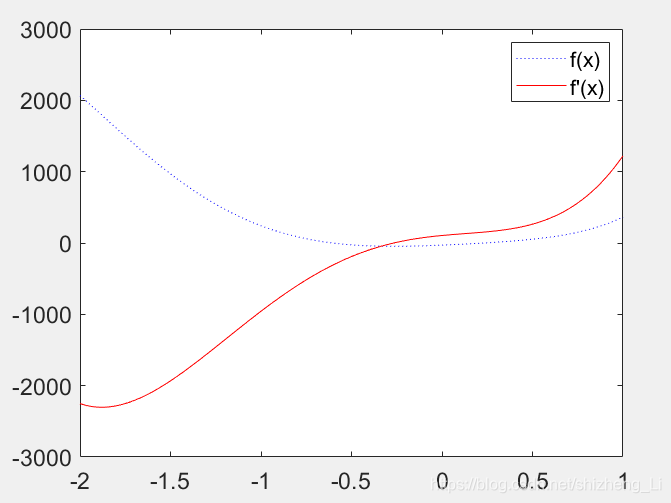
台湾国立大学郭彦甫Matlab教程笔记(14)polynomial differentiation多项式微分
台湾国立大学郭彦甫Matlab教程笔记(14) today: polynomial differentiation and integration多项式微分与积分 numerical differentiation and integration数值微分与积分 Differentiation微分 1.the derivative of a function f(x) is written a
R语言中的函数27:polynom::polynomial(), deriv(),integral(),solve()多式处理函数
文章目录 介绍polynomial()用法参数实例多项式的加减乘除等运算实例 deriv()和integral()用法参数实例solve()参数实例 介绍 R语言中的polynom包可以实现对多项式的操作,例如:加、减、乘、除、微分、积分。使用的时候先用polynomial()函数定义一个多项式对象,然后就可以相应的操作了。 polynomial() 用于创建一个多项式对象
针对zkVM中Memory Consistency Checks的Polynomial IOPs
1. 引言 主要参考Yuncong Zhang等人2023年论文《Polynomial IOPs for Memory Consistency Checks in Zero-Knowledge Virtual Machines》。 在设计zkvm时,需检查其所有组件的功能一致性,包括: instruction fetcher寄存器文件算术化逻辑单元内存 其中最具挑战的技术协议为Memory
ZKP7.2 Polynomial Commitments Based on Error-correcting Code
ZKP学习笔记 ZK-Learning MOOC课程笔记 Lecture 7: Polynomial Commitments Based on Error-correcting Codes (Yupeng Zhang) 7.2 Polyneomial commitment based on error-correcting codes Recall: polynomial commitm
ZKP7.1 Polynomial Commitments Based on Error-correcting Codes (Background)
ZKP学习笔记 ZK-Learning MOOC课程笔记 Lecture 7: Polynomial Commitments Based on Error-correcting Codes (Yupeng Zhang) Recall: common paradigm for efficient SNARK A polynomial commitment scheme + A polynomi
ZKP6.2 Discrete-log-based Polynomial Commitments (KZG10)
ZKP学习笔记 ZK-Learning MOOC课程笔记 Lecture 6: Discrete-log-based Polynomial Commitments (Yupeng Zhang) 6.2 KZG polynomial commitment and its variants KZG: [Kate-Zaverucha-Goldberg '2010]Procedure