本文主要是介绍【抱佛脚必备】18张图带你彻底搞定面试要考的数据结构!,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
点击上方"蓝字", 右上角选择“设为星标”
周一至周五早8点半!精品技术文章准时送上!
作者:嘉明
来源 | https://github.com/reng99/blogs
数据结构是计算机存储、组织数据的方式。数据结构是指相互直接存在一种或多种特殊关系的数据元素的集合。
通常情况下,精心选择数据结构可以带来更高的运行或者存储效率。作为一名程序猿,更需要了解下数据结构。
讲到数据结构,我们都会谈到线性结构和非线性结构。
1.线性结构是一个有序数据元素的集合。它应该满足下面的特征:
集合中必存在唯一的一个“第一个元素”
集合中必存在唯一的一个“最后的元素”
除最后一元素之外,其它数据元素均有唯一的“后继”
除第一个元素之外,其它数据元素均有唯一的“前驱”
按照百度百科的定义,我们知道符合条件的数据结构就有栈、队列和其它。
2.非线性结构其逻辑特征是一个节点元素可以有多个直接前驱或多个直接后继。
那么,符合条件的数据结构就有图、树和其它。
嗯~了解一下就行。我们进入正题:
数组
数组是一种线性结构,以十二生肖(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)排序为例:

我们来创建一个数组并打印出结果就一目了然了:
let arr = ['鼠', '牛', '虎', '兔', '龙', '蛇', '马', '羊', '猴', '鸡', '狗', '猪'];
arr.forEach((item, index) => {
console.log(`[ ${index} ] => ${item}`);
});
// [ 0 ] => 鼠
// [ 1 ] => 牛
// [ 2 ] => 虎
// [ 3 ] => 兔
// [ 4 ] => 龙
// [ 5 ] => 蛇
// [ 6 ] => 马
// [ 7 ] => 羊
// [ 8 ] => 猴
// [ 9 ] => 鸡
// [ 10 ] => 狗
// [ 11 ] => 猪
栈
栈是一种后进先出(LIFO)线性表,是一种基于数组的数据结构。(ps:其实后面讲到的数据结构或多或少有数组的影子)
LIFO(Last In First Out)表示后进先出,后进来的元素第一个弹出栈空间。类似于自动餐托盘,最后放上去的托盘,往往先被拿出来使用。
仅允许在表的一端进行插入和移除元素。这一端被称为栈顶,相对地,把另一端称为栈底。如下图的标识。
向一个栈插入新元素称作进栈、入栈或压栈,这是将新元素放在栈顶元素上面,使之成为新的栈顶元素。
从一个栈删除元素又称为出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。
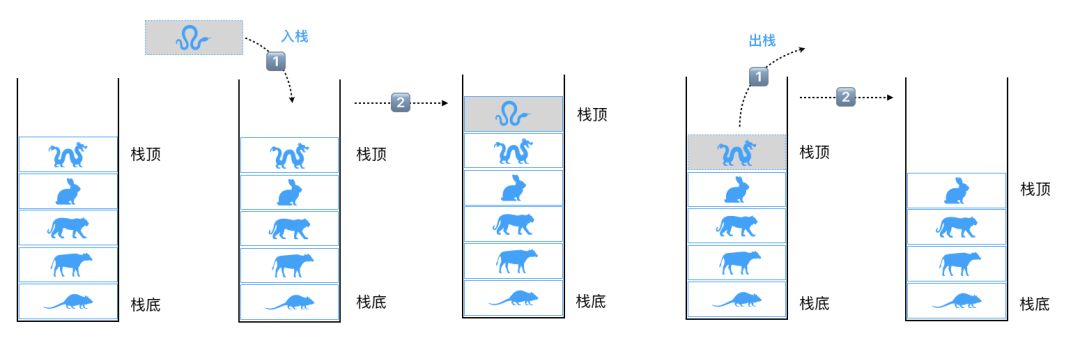
我们代码写下,熟悉下栈:
class Stack {
constructor(){
this.items = [];
}
// 入栈操作
push(element = ''){
if(!element) return;
this.items.push(element);
return this;
}
// 出栈操作
pop(){
this.items.pop();
return this;
}
// 对栈一瞥,理论上只能看到栈顶或者说即将处理的元素
peek(){
return this.items[this.size() - 1];
}
// 打印栈数据
print(){
return this.items.join(' ');
}
// 栈是否为空
isEmpty(){
return this.items.length == 0;
}
// 返回栈的元素个数
size(){
return this.items.length;
}
}
⚠️ 注意:栈这里的push和pop方法要和数组方法的push和pop方法区分下。
队列
队列是一种先进先出(FIFO)受限的线性表。受限体现在于其允许在表的前端(front)进行删除操作,在表的末尾(rear)进行插入【优先队列这些排除在外】操作。
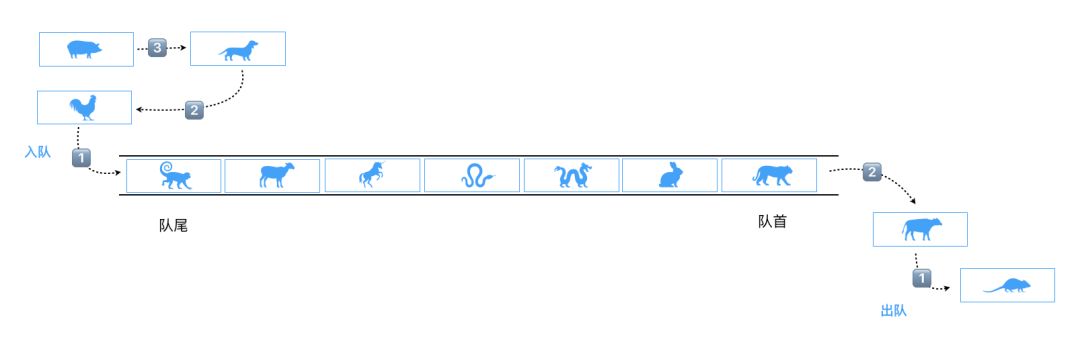
代码走一遍:
class Queue {
constructor(){
this.items = [];
}
// 入队操作
enqueue(element = ''){
if(!element) return;
this.items.push(element);
return this;
}
// 出队操作
dequeue(){
this.items.shift();
return this;
}
// 查看队前元素或者说即将处理的元素
front(){
return this.items[0];
}
// 查看队列是否为空
isEmpty(){
return this.items.length == 0;
}
// 查看队列的长度
len(){
return this.items.length;
}
// 打印队列数据
print(){
return this.items.join(' ');
}
}
链表
在进入正题之前,我们先来聊聊数组的优缺点。
优点:
存储多个元素,比较常用
访问便捷,使用下标[index]即可访问
缺点:
数组的创建通常需要申请一段连续的内存空间,并且大小是固定的(大多数的编程语言数组都是固定的),所以在进行扩容的时候难以掌控。
一般情况下,申请一个更大的数组,会是之前数组的倍数,比如两倍。然后,再将原数组中的元素复制过去
插入数据越是靠前,其成本很高,因为需要进行大量元素的位移。
相对数组,链表亦可以存储多个元素,而且存储的元素在内容中不必是连续的空间;
在插入和删除数据时,时间复杂度可以达到O(1)。
在查找元素的时候,还是需要从头开始遍历的,比数组在知道下标的情况下要快,但是数组如果不确定下标的话,那就另说了…
我们使用十二生肖来了解下链表:
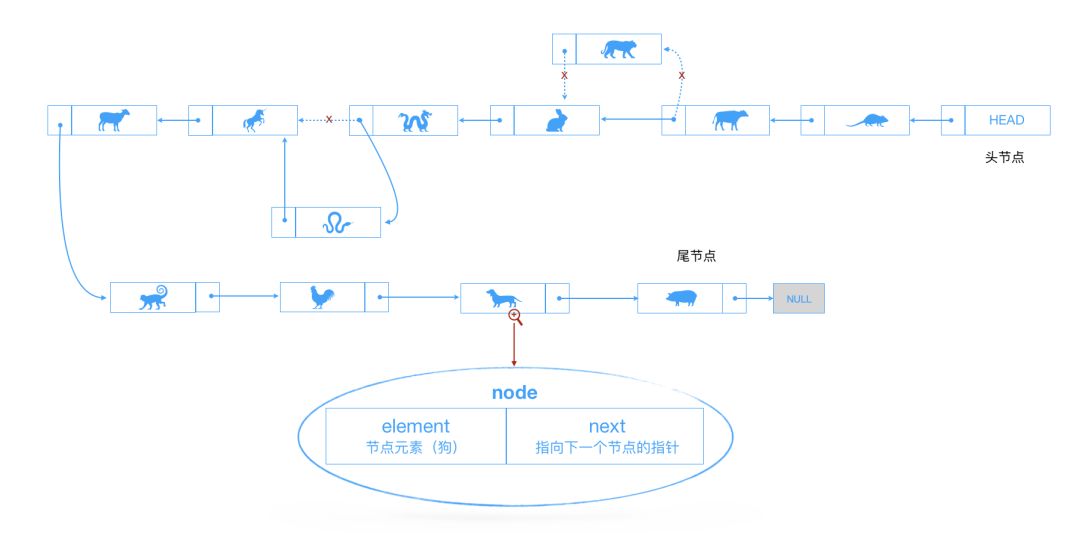
链表是由一组节点组成的集合。每个节点都使用一个对象的引用指向它的后继。如上图。下面用代码实现下:
// 链表
class Node {
constructor(element){
this.element = element;
this.next = null;
}
}
class LinkedList {
constructor(){
this.length = 0; // 链表长度
this.head = new Node('head'); // 表头节点
}
/**
* @method find 查找元素的功能,找不到的情况下直接返回链尾节点
* @param { String } item 要查找的元素
* @return { Object } 返回查找到的节点
*/
find(item = ''){
let currNode = this.head;
while(currNode.element != item && currNode.next){
currNode = currNode.next;
}
return currNode;
}
/**
* @method findPrevious 查找链表指定元素的前一个节点
* @param { String } item 指定的元素
* @return { Object } 返回查找到的之前元素的前一个节点,找不到节点的话返回链尾节点
*/
findPrevious(item){
let currNode = this.head;
while((currNode.next != null) && (currNode.next.element != item)){
currNode = currNode.next;
}
return currNode;
}
/**
* @method insert 插入功能
* @param { String } newElement 要出入的元素
* @param { String } item 想要追加在后的元素(此元素不一定存在)
*/
insert(newElement = '', item){
if(!newElement) return;
let newNode = new Node(newElement),
currNode = this.find(item);
newNode.next = currNode.next;
currNode.next = newNode;
this.length++;
return this;
}
// 展示链表元素
display(){
let currNode = this.head,
arr = [];
while(currNode.next != null){
arr.push(currNode.next.element);
currNode = currNode.next;
}
return arr.join(' ');
}
// 链表的长度
size(){
return this.length;
}
// 查看链表是否为空
isEmpty(){
return this.length == 0;
}
/**
* @method indexOf 查看链表中元素的索引
* @param { String } element 要查找的元素
*/
indexOf(element){
let currNode = this.head,
index = 0;
while(currNode.next != null){
index++;
if(currNode.next.element == element){
return index;
}
currNode = currNode.next;
}
return -1;
}
/**
* @method removeEl 移除指定的元素
* @param { String } element
*/
removeEl(element){
let preNode = this.findPrevious(element);
preNode.next = preNode.next != null ? preNode.next.next : null;
}
}
字典
字典的主要特点是键值一一对应的关系。可以比喻成我们现实学习中查不同语言翻译的字典。
这里字典的键(key)理论上是可以使用任意的内容,但还是建议语意化一点,比如下面的十二生肖图:
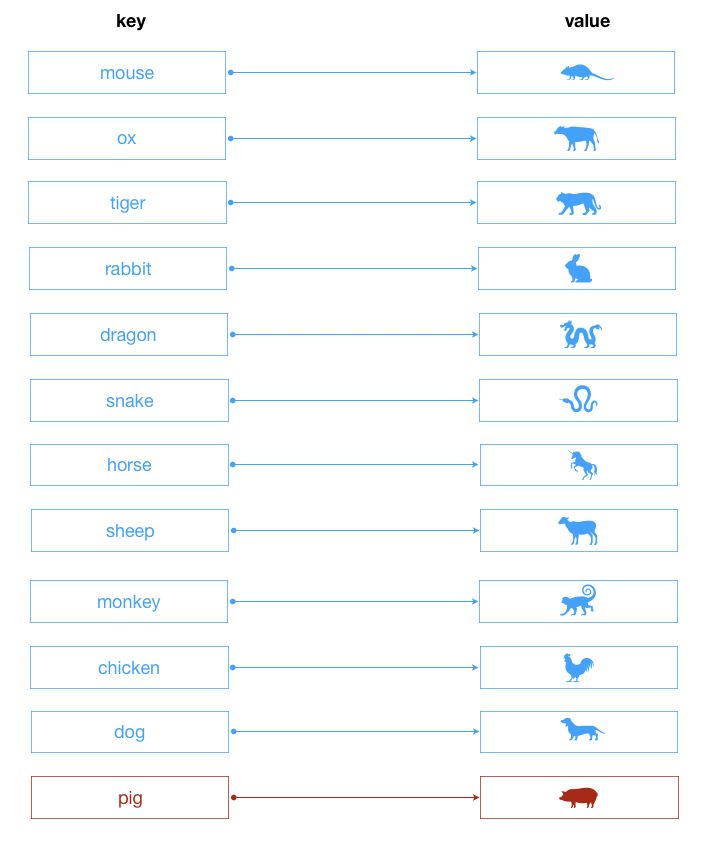
class Dictionary {
constructor(){
this.items = {};
}
/**
* @method set 设置字典的键值对
* @param { String } key 键
* @param {*} value 值
*/
set(key = '', value = ''){
this.items[key] = value;
return this;
}
/**
* @method get 获取某个值
* @param { String } key 键
*/
get(key = ''){
return this.has(key) ? this.items[key] : undefined;
}
/**
* @method has 判断是否含有某个键的值
* @param { String } key 键
*/
has(key = ''){
return this.items.hasOwnProperty(key);
}
/**
* @method remove 移除元素
* @param { String } key
*/
remove(key){
if(!this.has(key)) return false;
delete this.items[key];
return true;
}
// 展示字典的键
keys(){
return Object.keys(this.items).join(' ');
}
// 字典的大小
size(){
return Object.keys(this.items).length;
}
// 展示字典的值
values(){
return Object.values(this.items).join(' ');
}
// 清空字典
clear(){
this.items = {};
return this;
}
}
集合
集合通常是由一组无序的,不能重复的元素构成,一些常见的集合操作如图:
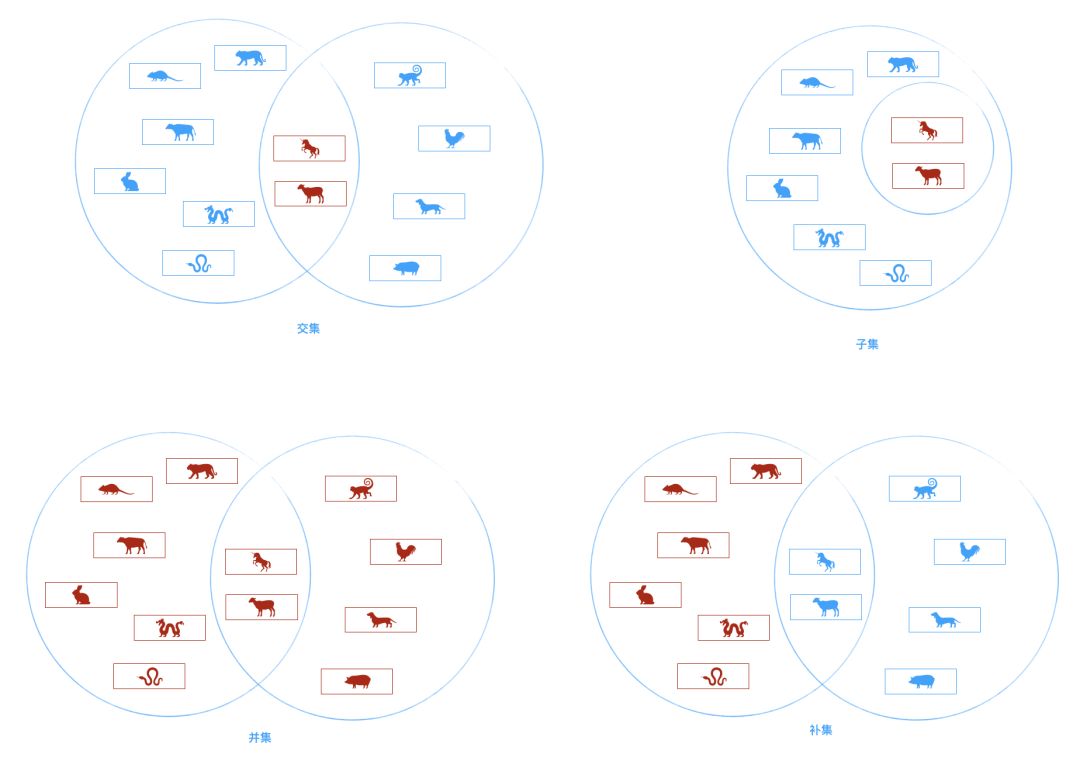
es6中已经封装好了可用的Set类。我们手动来写下相关的逻辑:
// 集合
class Set {
constructor(){
this.items = [];
}
/**
* @method add 添加元素
* @param { String } element
* @return { Boolean }
*/
add(element = ''){
if(this.items.indexOf(element) >= 0) return false;
this.items.push(element);
return true;
}
// 集合的大小
size(){
return this.items.length;
}
// 集合是否包含某指定元素
has(element = ''){
return this.items.indexOf(element) >= 0;
}
// 展示集合
show(){
return this.items.join(' ');
}
// 移除某个元素
remove(element){
let pos = this.items.indexOf(element);
if(pos < 0) return false;
this.items.splice(pos, 1);
return true;
}
/**
* @method union 并集
* @param { Array } set 数组集合
* @return { Object } 返回并集的对象
*/
union(set = []){
let tempSet = new Set();
for(let i = 0; i < this.items.length; i++){
tempSet.add(this.items[i]);
}
for(let i = 0; i < set.items.length; i++){
if(tempSet.has(set.items[i])) continue;
tempSet.items.push(set.items[i]);
}
return tempSet;
}
/**
* @method intersect 交集
* @param { Array } set 数组集合
* @return { Object } 返回交集的对象
*/
intersect(set = []){
let tempSet = new Set();
for(let i = 0; i < this.items.length; i++){
if(set.has(this.items[i])){
tempSet.add(this.items[i]);
}
}
return tempSet;
}
/**
* @method isSubsetOf 【A】是【B】的子集❓
* @param { Array } set 数组集合
* @return { Boolean } 返回真假值
*/
isSubsetOf(set = []){
if(this.size() > set.size()) return false;
this.items.forEach*(item => {
if(!set.has(item)) return false;
});
return true;
}
}
散列表/哈希表
散列是一种常用的存储技术,散列使用的数据结构叫做散列表/哈希表。
在散列表上插入、删除和取用数据都非常快,但是对于查找操作来说却效率低下,比如查找一组数据中的最大值和最小值。
查找的这些操作得求助其它数据结构,比如下面要讲的二叉树。
切入个案例感受下哈希表:
假如一家公司有1000个员工, 现在我们需要将这些员工的信息使用某种数据结构来保存起来。你会采用什么数据结构呢?
方案一:数组
按照顺序将所有员工信息依次存入一个长度为1000的数组中。每个员工的信息都保存在该数组的某个位置上。
但是我们要查看某个员工的信息怎么办呢?一个个查找吗?不太好找。
数组最大的优势是什么?通过下标值获取信息。
所以为了可以通过数组快速定位到某个员工,最好给员工信息中添加一个员工编号,而编号对应的就是员工的下标值。
当查找某个员工信息时,通过员工号可以快速定位到员工的信息位置。
方案二:链表
链表对应插入和删除数据有一定的优势。
但是对于获取员工的信息,每次都必须从头遍历到尾,这种方式显然不是特别适合我们这里。
最终方案:
这么看最终方案似乎就是数组了,但是数组还是有缺点,什么缺点呢?
假如我们想查看下张三这位员工的信息,但是我们不知道张三的员工编号,怎么办呢?
当然,我们可以问他的员工编号。但是我们每查找一个员工都是要问一下这个员工的编号吗?不合适。【那我们还不如直接问他的信息嘞】
能不能有一种办法,让张三的名字和他的员工编号产生直接的关系呢?
也就是通过张三这个名字,我们就能获取到他的索引值,而再通过索引值我们就能获取张三的信息呢?
这样的方案已经存在了,就是使用哈希函数,让某个key的信息和索引值对应起来。
那么散列表的原理和实现又是怎样的呢,我们来聊聊。
我们的哈希表是基于数组完成的,我们从数组这里切入解析下。数组可以通过下标直接定位到相应的空间,哈希表的做法就是类似的实现。
哈希表把key(键)通过一个固定的算法函数(此函数称为哈希函数/散列函数)转换成一个整型数字。
然后,就将该数字对数组长度进行取余,取余结果就当作数组的下标,将value(值)存储在以该数字为下标的数组空间里。
而当使用哈希表进行查询的时候,就是再次使用哈希函数将key转换为对应的数组下标,并定位到该空间获取value。
结合下面的代码,也许你会更容易理解:
// 哈希表
class HashTable {
constructor(){
this.table = new Array(137);
}
/**
* @method hashFn 哈希函数
* @param { String } data 传入的字符串
* @return { Number } 返回取余的数字
*/
hashFn(data){
let total = 0;
for(let i = 0; i < data.length; i++){
total += data.charCodeAt(i);
}
return total % this.table.length;
}
/**
*
* @param { String } data 传入的字符串
*/
put(data){
let pos = this.hashFn(data);
this.table[pos] = data;
return this;
}
// 展示
show(){
this.table && this.table.forEach((item, index) => {
if(item != undefined){
console.log(index + ' => ' + item);
}
})
}
// ...获取值get函数等看官感兴趣的话自己补充测试啦
}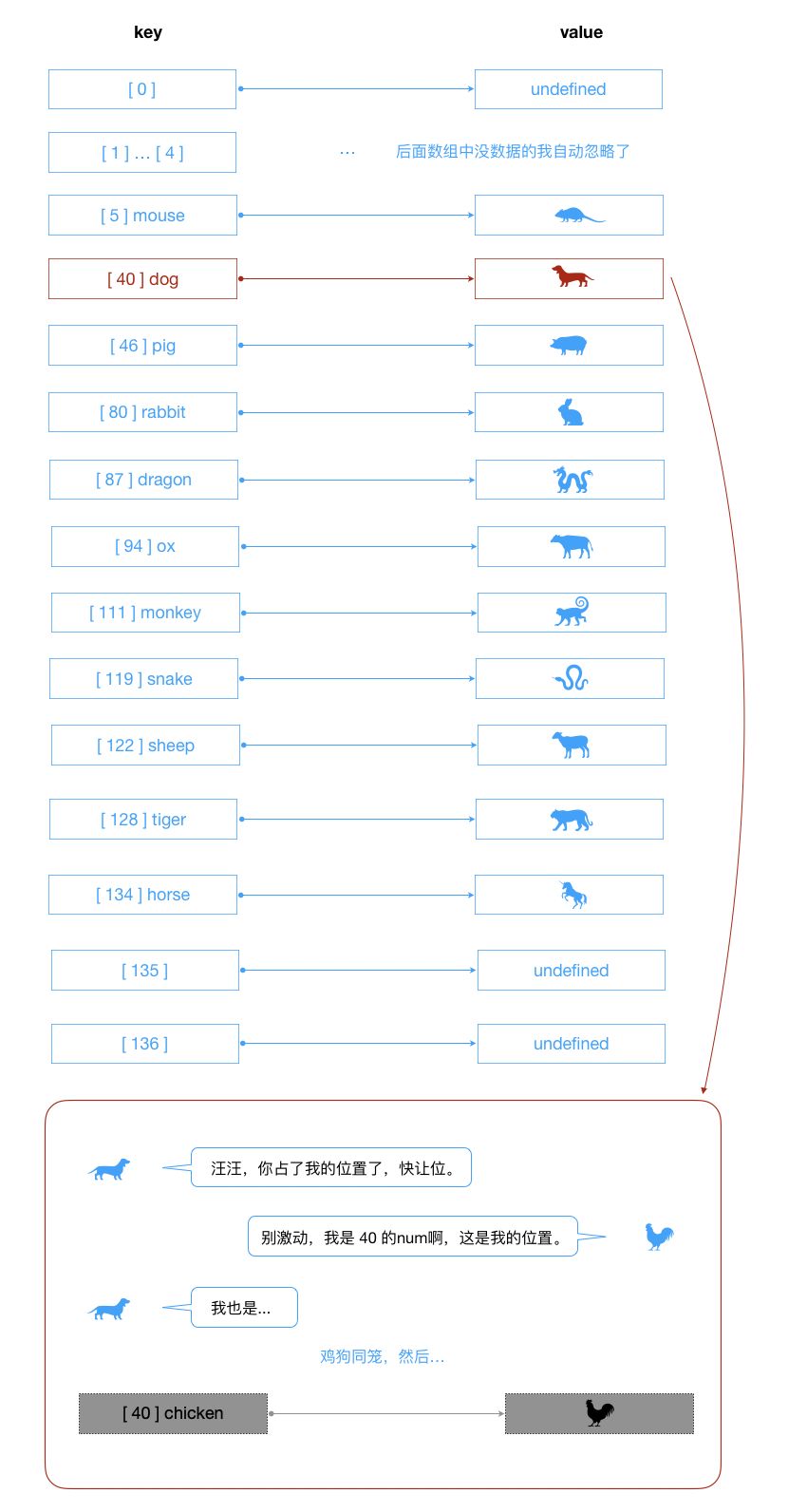
针对上面的问题,我们存储数据的时候,产生冲突的话我们可以像下面这样解决:
1. 线性探测法
当发生碰撞(冲突)时,线性探测法检查散列表中的下一个位置【有可能非顺序查找位置,不一定是下一个位置】是否为空。
如果为空,就将数据存入该位置;如果不为空,则继续检查下一个位置,直到找到一个空的位置为止。
该技术是基于一个事实:每个散列表都有很多空的单元格,可以使用它们存储数据。
2. 开链法
但是,当发生碰撞时,我们任然希望将key(键)存储到通过哈希函数产生的索引位置上,那么我们可以使用开链法。
开链法是指实现哈希表底层的数组中,每个数组元素又是一个新的数据结构,比如另一个数组(这样结合起来就是二位数组了),链表等,这样就能存储多个键了。
使用这种技术,即使两个key(键)散列后的值相同,依然是被保存在同样的位置,只不过它们是被保存在另一个数据结构上而已。
以另一个数据结构是数组为例,存储的数据如下:
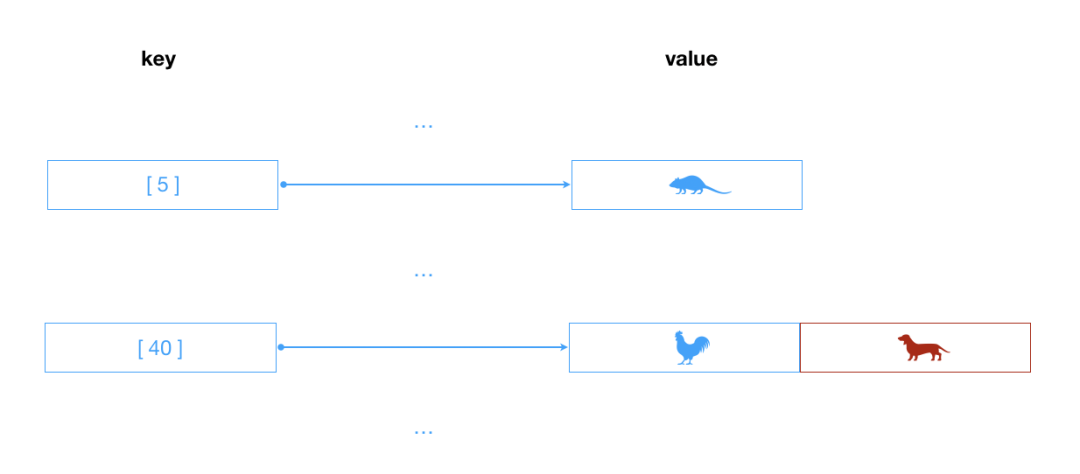
二叉查找树
树的定义:
树(Tree):
n(n >= 0)个节点构成的有限集合。当`n = 0`时,称为空树;
对任意一棵空树`(n > 0)`,它具备以下性质:
树中有一个称为根(Root)的特殊节点,用`r(root)`表示;
其余节点可分为`m(m > 0)`个互不相交的有限集`T1,T2,…Tm`,其中每个集合本省又是一棵树,称为原来树的子树(SubTree)
注意:
子树之间`不可以相交`;
除了根节点外,每个节点有且仅有一个父节点;
一个`N`个节点的树有`N-1`条边。
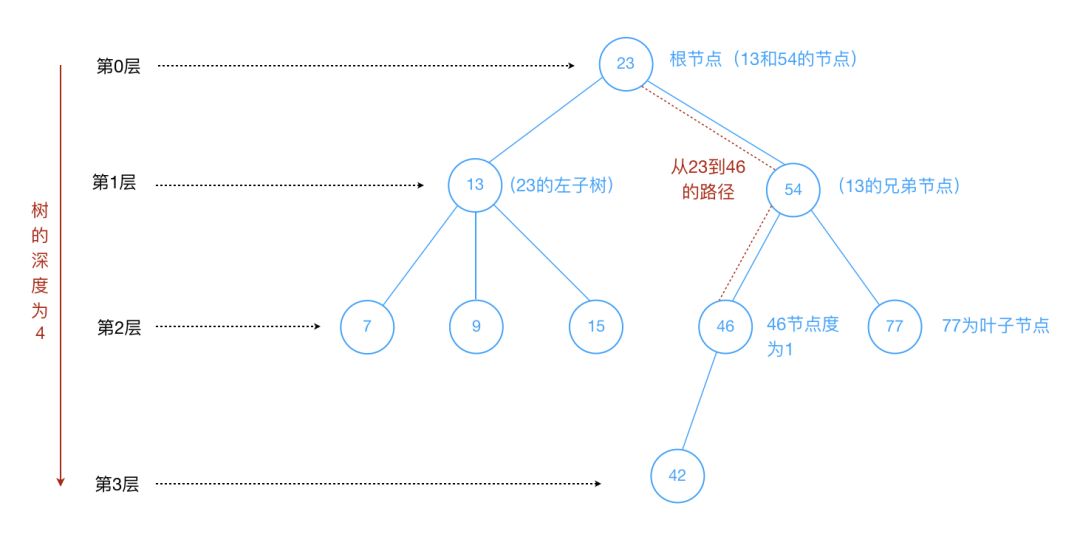
树的术语:
节点的度(Degree):节点的子树个数。
树的度:树的所有节点中最大的度数(树的度通常为节点个数的N-1)。
叶节点(Leaf):度为0的节点(也称叶子节点)。
父节点(Parent):有子树的节点是其子树的父节点。
子节点(Child):若A节点是B节点的父节点,则称B节点是A节点的子节点。
兄弟节点(Sibling):具有同一个父节点的各节点彼此是兄弟节点。
路径和路径长度:从节点n1到nk的路径为一个节点序列n1,n2,n3,…,nk,ni是ni+1的父节点。路径所包含边的个数为路径长度。
节点的层次(Level):规定根节点在第0层,它的子节点是第1层,子节点的子节点是第2层,以此类推。
树的深度(Depth):树中所有节点中的最大层次是这棵树的深度(因为上面是从第0层开始,深度 = 第最大层数 + 1)
如下图:
二叉树的定义:
二叉树可以为空,也就是没有节点
二叉树若不为空,则它是由根节点和称为其左子树
TL和右子树RT的两个不相交的二叉树组成二叉树每个节点的子节点不允许超过
两个二叉树的五种形态:
空
只有根节点
只有左子树
只有右子树
左右子树均有
对应下图(从左至右):
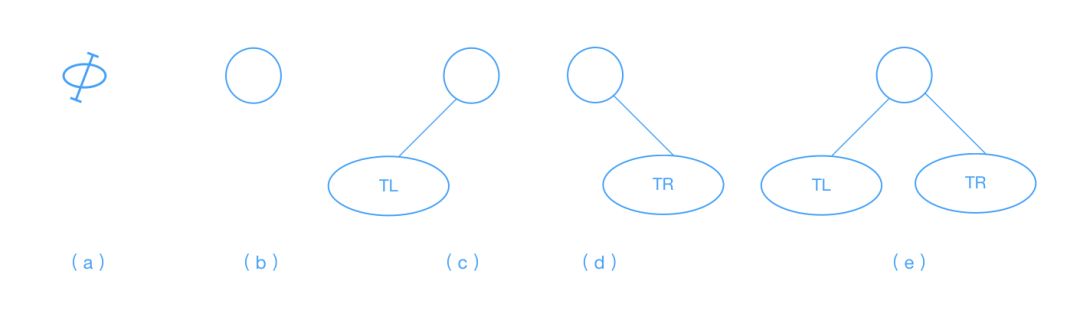
我们接下来要讲的是二叉查找树(BST,Binary Search Tree)。
二叉查找树,也称二叉搜索树或二叉排序树,是一种特殊的二叉树,相对值较小的值保存在左节点中,较大的值保存在右节点中。
二叉查找树特殊的结构使它能够快速的进行查找、插入和删除数据。
下面我们来实现下:
// 二叉查找树
// 辅助节点类
class Node {
constructor(data, left, right){
this.data = data;
this.left = left;
this.right = right;
}
// 展示节点信息
show(){
return this.data;
}
}
class BST {
constructor(){
this.root = null;
}
// 插入数据
insert(data){
let n = new Node(data, null, null);
if(this.root == null){
this.root = n;
}else{
let current = this.root,
parent = null;
while(true){
parent = current;
if(data < current.data){
current = current.left;
if(current == null){
parent.left = n;
break;
}
}else{
current = current.right;
if(current == null){
parent.right = n;
break;
}
}
}
}
return this;
}
// 中序遍历
inOrder(node){
if(!(node == null)){
this.inOrder(node.left);
console.log(node.show());
this.inOrder(node.right);
}
}
// 先序遍历
preOrder(node){
if(!(node == null)){
console.log(node.show());
this.preOrder(node.left);
this.preOrder(node.right);
}
}
// 后序遍历
postOrder(node){
if(!(node == null)){
this.postOrder(node.left);
this.postOrder(node.right);
console.log(node.show());
}
}
// 获取最小值
getMin(){
let current = this.root;
while(!(current.left == null)){
current = current.left;
}
return current.data;
}
// 获取最大值
getMax(){
let current = this.root;
while(!(current.right == null)){
current = current.right;
}
return current.data;
}
// 查找给定的值
find(data){
let current = this.root;
while(current != null){
if(current.data == data){
return current;
}else if(data < current.data){
current = current.left;
}else{
current = current.right;
}
}
return null;
}
// 移除给定的值
remove(data){
root = this.removeNode(this.root, data);
return this;
}
// 移除给定值的辅助函数
removeNode(node, data){
if(node == null){
return null;
}
if(data == node.data){
// 叶子节点
if(node.left == null && node.right == null){
return null; // 此节点置空
}
// 没有左子树
if(node.left == null){
return node.right;
}
// 没有右子树
if(node.right == null){
return node.left;
}
// 有两个子节点的情况
let tempNode = this.getSmallest(node.right); // 获取右子树
node.data = tempNode.data; // 将其右子树的最小值赋值给删除的那个节点值
node.right = this.removeNode(node.right, tempNode.data); // 删除指定节点的下的最小值,也就是置其为空
return node;
}else if(data < node.data){
node.left = this.removeNode(node.left, data);
return node;
}else{
node.right = this.removeNode(node.right, data);
return node;
}
}
// 获取给定节点下的二叉树最小值的辅助函数
getSmallest(node){
if(node.left == null){
return node;
}else{
return this.getSmallest(node.left);
}
}
}
看了上面的代码之后,你是否有些懵圈呢?我们借助几张图来了解下,或许你就豁然开朗了。
在遍历的时候,我们分为三种遍历方法--先序遍历,中序遍历和后序遍历:
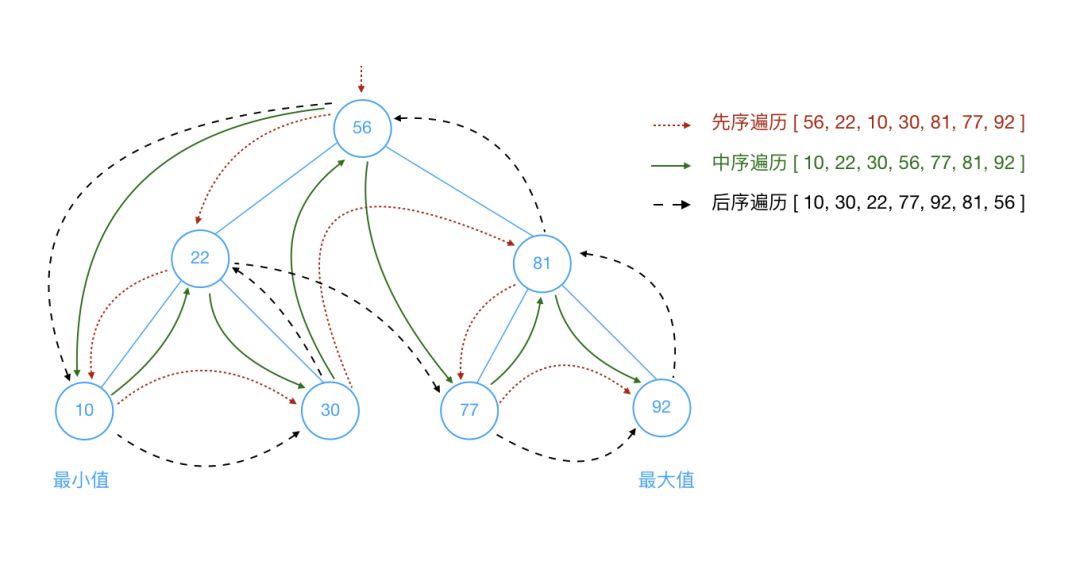
删除节点是一个比较复杂的操作,考虑的情况比较多:
该节点没有叶子节点的时候,直接将该节点置空;
该节点只有左子树,直接将该节点赋予左子树
该节点只有右子树,直接将该节点赋予右子树
该节点左右子树都有,有两种方法可以处理
方案一:从待删除节点的
左子树找节点值最大的节点A,替换待删除节点值,并删除节点A方案二:从待删除节点的
右子树找节点值最小的节点A,替换待删除节点值,并删除节点A【?上面的示例代码中就是这种方案】
删除两个节点的图解如下:
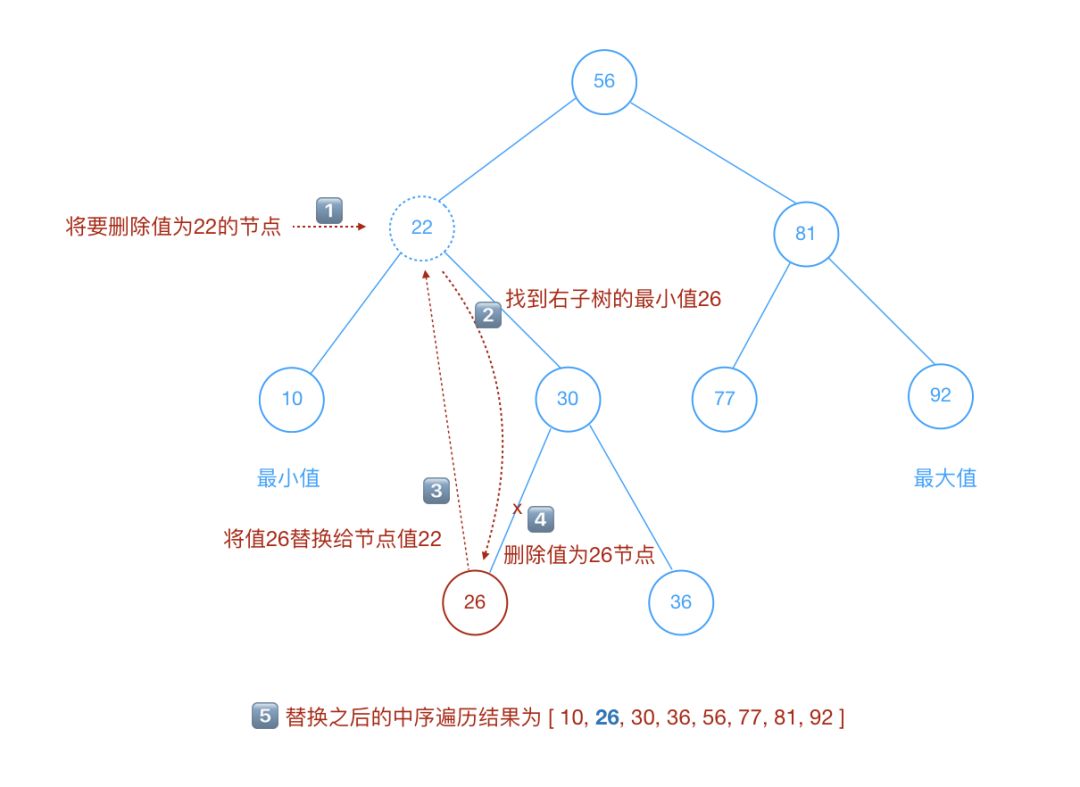
图
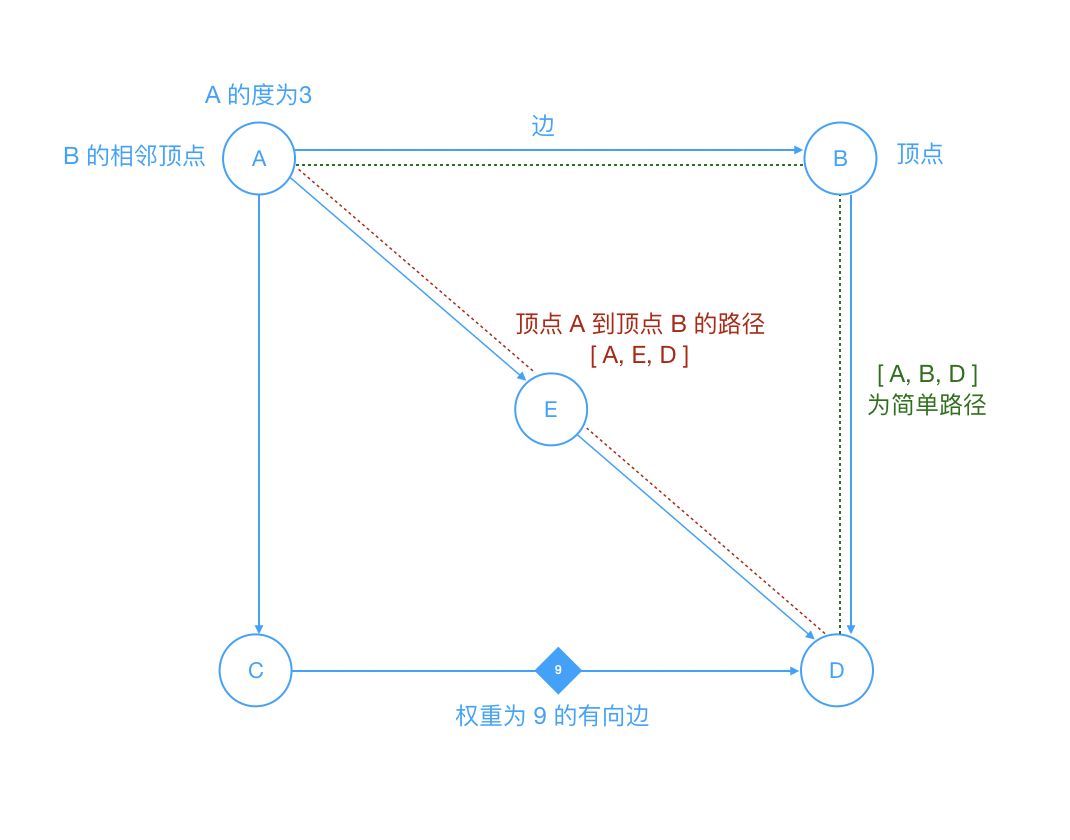
图由边的集合及顶点的集合组成。
我们来了解下图的相关术语:
顶点:图中的一个节点。
边:表示顶点和顶点之间的连线。
相邻顶点:由一条边连接在一起的顶点称为相邻顶点。
度:一个顶点的度是相邻顶点的数量。比如
0顶点和其它两个顶点相连,0顶点的度就是2路径:路径是顶点
v1,v2...,vn的一个连续序列。
简单路径:简单路径要求不包含重复的顶点。
回路:第一个顶点和最后一个顶点相同的路径称为回路。
有向图和无向图
有向图表示图中的
边是有方向的。无向图表示图中的
边是无方向的。带权图和无权图
带权图表示图中的边
有权重。无权图表示图中的边
无权重。
如下图:
图可以用于现实中的很多系统建模,比如:
对交通流量建模
顶点可以表示街道的十字路口, 边可以表示街道.
加权的边可以表示限速或者车道的数量或者街道的距离.
建模人员可以用这个系统来判定最佳路线以及最可能堵车的街道.
图既然这么方便,我们来用代码实现下:
// 图
class Graph{
constructor(v){
this.vertices = v; // 顶点个数
this.edges = 0; // 边的个数
this.adj = []; // 邻接表或邻接表数组
this.marked = []; // 存储顶点是否被访问过的标识
this.init();
}
init(){
for(let i = 0; i < this.vertices; i++){
this.adj[i] = [];
this.marked[i] = false;
}
}
// 添加边
addEdge(v, w){
this.adj[v].push(w);
this.adj[w].push(v);
this.edges++;
return this;
}
// 展示图
showGraph(){
for(let i = 0; i < this.vertices; i++){
for(let j = 0; j < this.vertices; j++){
if(this.adj[i][j] != undefined){
console.log(i +' => ' + this.adj[i][j]);
}
}
}
}
// 深度优先搜索
dfs(v){
this.marked[v] = true;
if(this.adj[v] != undefined){
console.log("visited vertex: " + v);
}
this.adj[v].forEach(w => {
if(!this.marked[w]){
this.dfs(w);
}
})
}
// 广度优先搜索
bfs(v){
let queue = [];
this.marked[v] = true;
queue.push(v); // 添加到队尾
while(queue.length > 0){
let v = queue.shift(); // 从对首移除
if(v != undefined){
console.log("visited vertex: " + v);
}
this.adj[v].forEach(w => {
if(!this.marked[w]){
this.marked[w] = true;
queue.push(w);
}
})
}
}
}
对于搜索图,在上面我们介绍了深度优先搜索 - DFS(Depth First Search)和广度优先搜索 - BFS(Breadth First Search)
结合下面的图再回头看下上面的代码,你会更加容易理解这两种搜索图的方式。
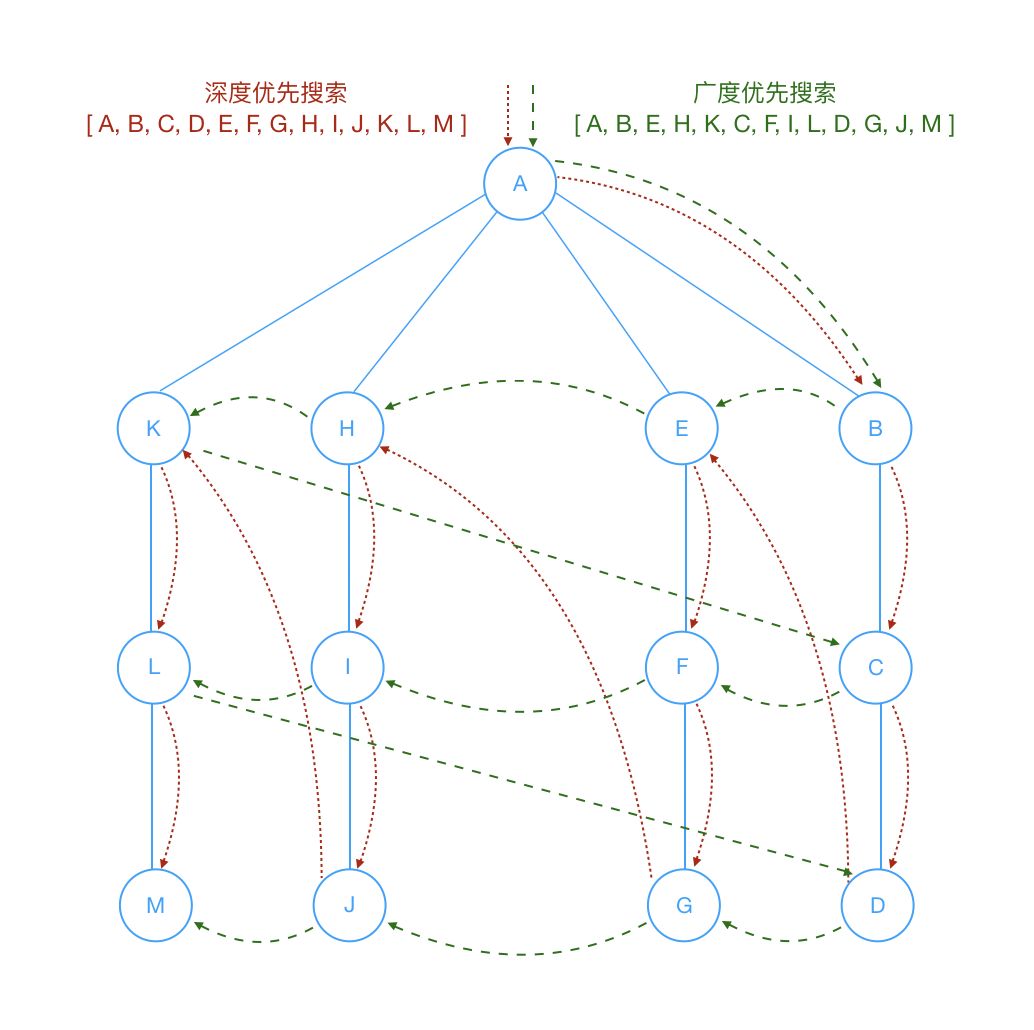
End

公众号后台回复“学习”,获取作者独家秘制学习资料
还没读够?更多原创系列文章,请移步至
2018年原创汇总
2019年原创汇总(持续更新)
面试专栏
爆款推荐

持续关注,一大波原创系列文章正在路上
欢迎扫描下方二维码

石杉的架构笔记(id:shishan100)
BAT架构经验倾囊相授

这篇关于【抱佛脚必备】18张图带你彻底搞定面试要考的数据结构!的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








