现有一个m * n的网格，从最左上角出发，每次只能向右或者向下移动一格，问有多少种不同的方法可以到达最右下角的格子

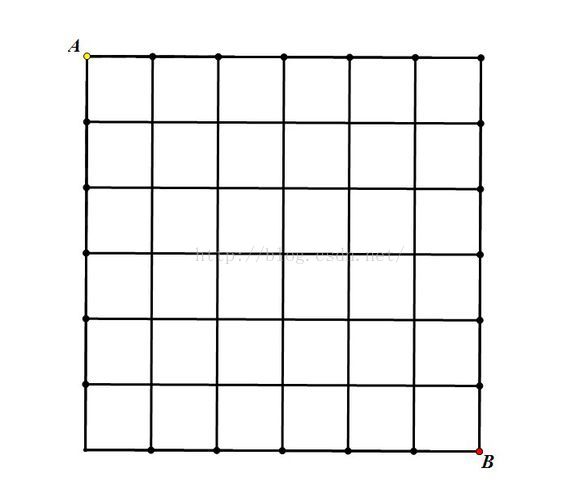
   可以用高中学过的排列组合来解，见下图一个6*6的格子，从A走到B:

   要从A到B，必须向左走6步，向下也走6步，一共12步，我们可以从向下走入手，向下走的方法即从12步里选出6步向下，一共有C(12,6)种，因此从A到B的路线共有组合数C(12,6)种。

   对于m*n的格子，一样的，就是从m+n步中选出m步向下或n步向右，因此为C(m+n,m)=C(m+n,n)种。

   简单编程即可得到。

#include<stdio.h>
int n,m,dp[10005][10005];
int main()
{while(~scanf("%d%d",&n,&m)){dp[0][0]=0;for(int i=1; i<=n; i++)dp[i][0]=1;for(int j=1; j<=m; j++)dp[0][j]=1;//初始化for(int i=1; i<=n; i++)for(int j=1; j<=m; j++){dp[i][j]=dp[i-1][j]+dp[i][j-1];//动态规划转移方程}printf("%d\n",dp[n][m]);}return 0;
}

//2.递归
#include <stdio.h>
long long p(int a,int b,int c)
{if(b == 1 || c == 1){return 1;}else{return p(a-2,b-1,c-1)*(a-2)*(a-3)/(c-1)/(c-1);}
}
int main()
{int m,n;while(scanf("%d%d",&m,&n)!= EOF)printf("%d\n",p(m + n,m,n));return 0;
}

//3.递归
#include <stdio.h>
long long compute(int n,int k)
{if(k == 0){return 1;}else{return(n*compute(n-1,k-1))/k;}
}
int uniquePaths(int m,int n)
{return compute(m+n-2,m-1);
}
int main()
{int m,n;while(scanf("%d%d",&m,&n)!= EOF)printf("%d\n",uniquePaths(m,n));return 0;
}