本文主要是介绍ZC序列理论学习及仿真,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 前言
- 一、ZC 序列理论
- 1、基本概念
- 2、表达式
- 3、ZC 序列一些定义
- ①、自相关
- ②、循环移位
- ③、循环自相关
- ④、循环互相关
- 二、ZC 序列性质
- 1、性质 1:恒包络,即等模
- 2、性质 2:零循环自相关
- 3、性质 3:固定循环互相关
- 4、其他性质
- ①、傅里叶变换后仍是 ZC 序列
- ②、低峰均比
- ③、序列间的正交性
- 三、MATLAB 仿真
- 1、ZC 序列生成
- ①、复数点
- ②、复平面散点图
- ③、模值
- 2、ZC 序列循环移位
- 3、ZC 序列自相关函数
- 4、ZC 序列循环自相关
- 5、ZC 序列循环互相关
- 6、ZC 序列傅里叶变换
- 7、ZC 序列低峰均比特性
前言
ZC 序列和 m 序列是数字通信中常用的两种序列,在编码和解码过程中起到重要的作用。本文作为 ZC 序列学习笔记,主要研究 ZC 序列的一些性质,并通过 MATLAB 对其进行仿真验证。
一、ZC 序列理论
1、基本概念
ZC 序列(Zadoff-Chu 序列)是一种具有良好性质的离散序列,它是一种复数序列,在通信系统中广泛应用。它由 Zadoff 和 Chu 于 1964 年提出,是一种特殊的线性调频脉冲压缩序列。ZC 序列常用于通信系统中的同步和信道估计等方面。
- ZC 序列的自相关性是指序列与其自身进行相关运算后的结果。自相关性能够体现序列的周期性和重复性,对于同步和信道估计非常重要。
- ZC 序列的互相关性是指序列与其他序列进行相关运算后的结果。互相关性能够体现序列之间的相似程度,对于信道估计和多用户检测等方面有着重要作用。
ZC 序列常用于各种无线通信系统中,如 LTE(Long Term Evolution)、WiMAX(Worldwide Interoperability for Microwave Access)、GNSS(Global Navigation Satellite System)等。它们被广泛应用于信号处理和通信领域,以提高系统性能和可靠性。
2、表达式
ZC 序列常用于随机接入(Random Access)中以生成 preamble 序列,其表达式如下图所示:
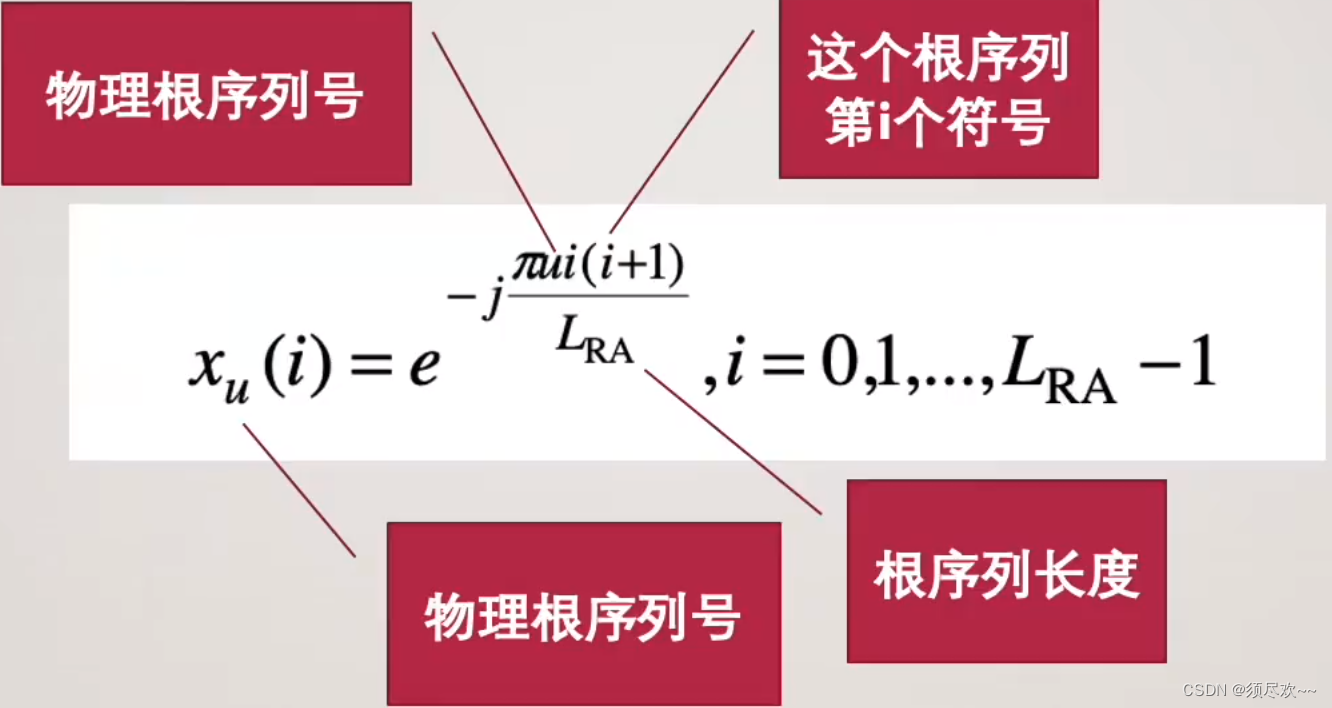
ZC 序列有两个重要的参数:
根索引(root index):对应上图中物理根序列号 u u u, u u u 是由逻辑根序列号查表获取;ZC 序列的长度:对应上图中根序列长度 L R A L_{RA} LRA,一定得是奇数(常常是质数);
对于任意 ZC 序列,在长度 L R A L_{RA} LRA 和根序列 u u u 的取值确定的情况下,便可确定根序列 i i i。
注意到:每个 ZC 序列的长度为 L R A L_{RA} LRA,而ZC序列的序列空间大小为 L R A − 1 L_{RA}-1 LRA−1,即一共有 L R A − 1 L_{RA}-1 LRA−1 个 ZC 序列。
我们可以发现,ZC 序列的值是一个复数,由欧拉公式 e j α = c o s ( α ) + j s i n ( α ) e^{j\alpha}=cos(\alpha)+jsin(\alpha) ejα=cos(α)+jsin(α),即可得到该复数的实部和虚部,除此之外,还可以发现它的幅值恒为 1,其实在复数坐标系中,它都是在单位圆上。
3、ZC 序列一些定义
①、自相关
离散时间序列的自相关函数定义为:
R n = ∑ n = − ∞ ∞ x [ k ] x ∗ [ k + n ] R_{n}= \sum\limits_{n=-\infty}^{\infty}x[k]x^{*}[k+n] Rn=n=−∞∑∞x[k]x∗[k+n]
- x [ k ] x[k] x[k] 为调制序列;
- x ∗ [ k + n ] x^{*}[k+n] x∗[k+n] 为 x [ k ] x[k] x[k] 时延信号的共轭。
②、循环移位
一个长度为 N N N 的有限长序列 x [ n ] x[n] x[n],其 m 次循环移位公式如下:
x m [ n ] = x [ ( n + m ) m o d N ] , m = 0 , 1 , 2 , . . . , N − 1 x^{m}[n]=x[(n+m)\ mod\ N],m=0,1,2,...,N-1 xm[n]=x[(n+m) mod N],m=0,1,2,...,N−1
一共有 N N N 个循环移位序列(包括本身)。
③、循环自相关
循环自相关也叫周期自相关,长度为 N N N 的有限长序列 x [ n ] x[n] x[n] 的序列循环自相关公式为:
R 0 = ∑ n = 0 N − 1 x [ n ] x ∗ [ n ] R_{0}=\sum^{N-1}_{n=0}x[n]x^{*}[n] R0=n=0∑N−1x[n]x∗[n]
归一化的循环自相关公式为:
R ‾ x x [ τ ] = 1 N R x x [ τ ] \overline{R}_{xx}[\tau]=\frac{1}{N}R_{xx}[\tau] Rxx[τ]=N1Rxx[τ]
显而易见, R ‾ x x [ 0 ] = 1 , R ‾ x x [ τ ≠ 0 ] ≤ 1 \overline{R}_{xx}[0]=1,\overline{R}_{xx}[\tau \neq0]\le1 Rxx[0]=1,Rxx[τ=0]≤1。
④、循环互相关
循环互相关也叫周期互相关,给定长度为 N N N 的两个有限长序列 x [ n ] x[n] x[n] 和 y [ n ] y[n] y[n],它们的循环互相关公式为:
R x y = ∑ n = 0 N − 1 x [ n ] y ∗ [ n ] R_{xy}=\sum^{N-1}_{n=0}x[n]y^{*}[n] Rxy=n=0∑N−1x[n]y∗[n]
类似地,我们可以定义归一化的循环互相关公式为:
R ‾ x y [ τ ] = 1 N R x y [ τ ] \overline{R}_{xy}[\tau]=\frac{1}{N}R_{xy}[\tau] Rxy[τ]=N1Rxy[τ]
一般地,我们把 R ‾ x y [ 0 ] \overline{R}_{xy}[0] Rxy[0] 称为两个序列的互相关。
二、ZC 序列性质
1、性质 1:恒包络,即等模
任意长度的 ZC 序列幅值恒定,这也意味着功率恒定,这个好处就是射频器件不用忽大忽小的改变放大能量。为什么能够恒包络?看 ZC 序列的生成表达可以看到,本质就是一个底数为 e 的指数序列,每一个序列值代表单位圆上的一个点。每一个点值,仅是改变相位而已。复指数是一个二维 I、Q 的平面图。
令 u = 10 u=10 u=10, L R A = 839 L_{RA} = 839 LRA=839,绘制的复平面图形如下:
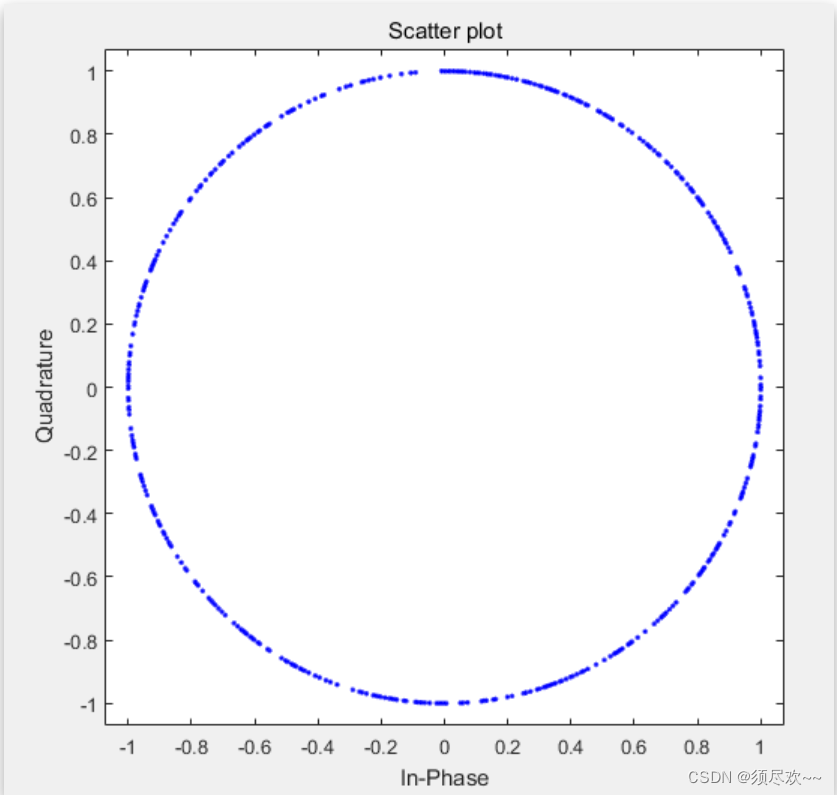
2、性质 2:零循环自相关
一个 ZC 序列的循环自相关是最优的,因为对于所有的非零移位序列,与原序列的自相关都等于 0
ZC 序列循环移位 N,如果 N 不等于 ZC 序列的长度(N 等于序列长度,循环移位后回到起始点了),则移位后的序列和原序列不相关。啥意思?就是说虽然本是同根生,但是只要屁股挪了一下,哪怕是挪一位,那长得一点都不像没有挪前的样子。这个性质有什么好处?假如没挪前的序列表示一个 UE,挪位后的序列表示另一个 UE,那么基站用根序列与接收到的序列一相关运算,就知道有几个 UE 在向他打报告申请资源了。至于“相关”运算,可以理解为查看两条序列长得“像不像”的工具,长得“像”,相关峰值就又直又高耸入云,长得不“像”,相关峰值就软绵绵趴在地上。
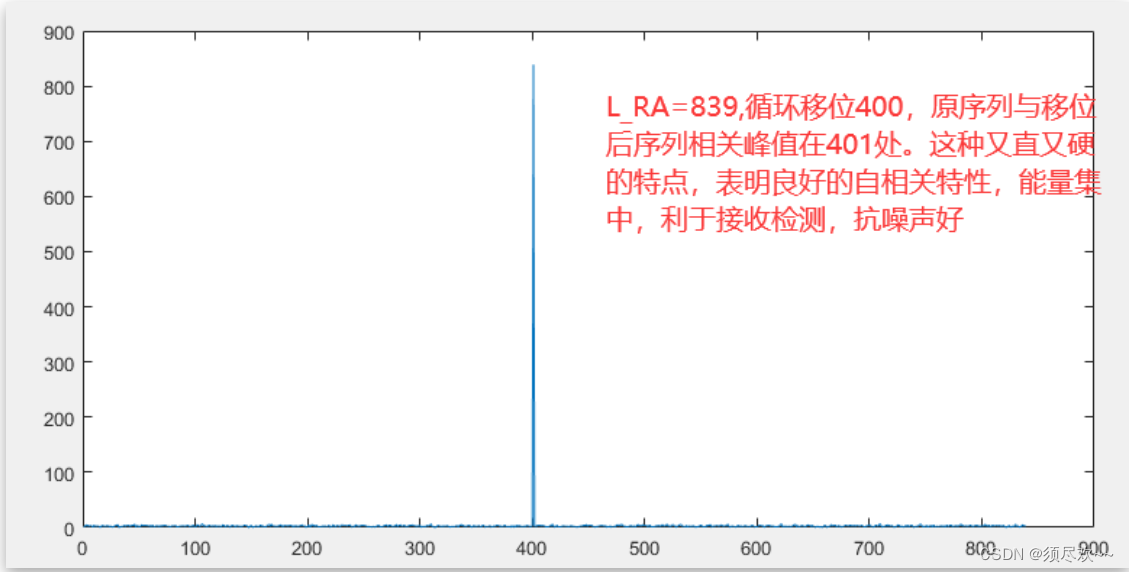
ZC 序列循环移位后,原序列和移位后的相关峰值出现在移位大小的位置。
3、性质 3:固定循环互相关
对相同长度的两个 ZC 序列,即一个序列的 root index 为 q 1 q_1 q1,另一个序列的 root index 为 q 2 q_2 q2,且 q 1 ≠ q 2 q_1\neq q_2 q1=q2,那么两个序列的归一化循环互相关值正好等于 1 / N z c 1/\sqrt{N_{zc}} 1/Nzc,这里一般假设 N z c N_{zc} Nzc 是质数,或者更一般地,认为 ∣ q 1 − q 2 ∣ |q_1-q_2| ∣q1−q2∣ 与 N z c N_{zc} Nzc 互质。
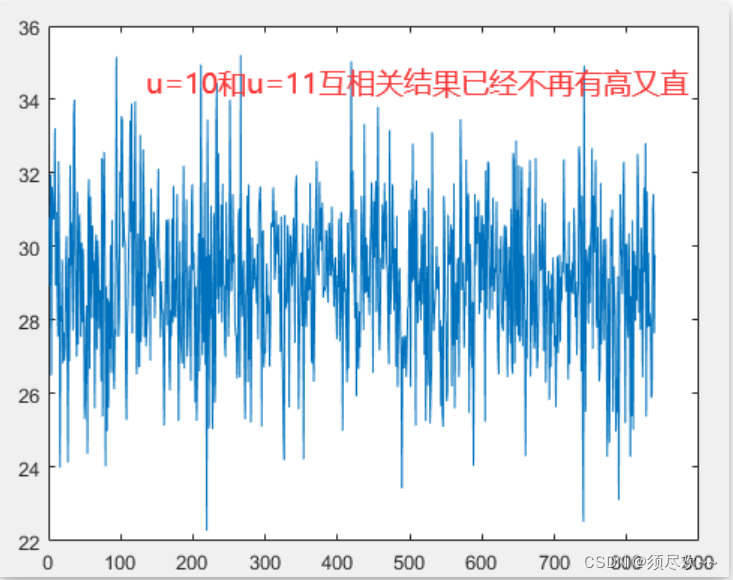
4、其他性质
①、傅里叶变换后仍是 ZC 序列
这个性质,简直就是为 OFDM 系统量身打造,也省去多少运算量。既可以在时域相关,也可以在频域相关,灵活决定姿势,怎么方便怎么来。
OFDM 本质是多个并行的子载波采用正交 IQ 调制,然后相加在一起,以单个子载波对应的时间周期T,离散化后,刚好是一个离散逆傅立叶变换IFFT,这是 OFDM 调制采用 IFFT 变换的本质。
②、低峰均比
对于发端,ZC 序列峰均比低(ZC 序列时频域都是 ZC 序列,且幅值恒定),有利于射频功放信号发挥最大的效率。
对于信道估计,ZC 序列幅值恒定,其图形可看作一个单位圆。
序列长度对序列的影响:ZC 序列越长,序列间的互相关性越差。在做多用户 RA 时,序列间的互相关性越差,某一序列对其他序列造成的干扰越小,从而提高序列检测的正确率。因此,ZC序列越长,检测性能越好。
③、序列间的正交性
- 相同 root index 的两个 ZC 序列彼此正交;
- 不同 root index 的两个 ZC 序列由于其彼此互相关性非零,因此不再具有正交性;
三、MATLAB 仿真
1、ZC 序列生成
MATLAB 上已经有函数专门产生 ZC 序列的函数:zadoffChuSeq
注:zadoffChuSeq 用在 R2019a 版本及以后,之前的版本使用 lteZadoffChuSeq 函数,这两个函数只是名字发生了变化。
使用方法:
seq = zadoffChuSeq(R,N) % 生成长度为 N 的第 R 根的 Zadoff-Chu 序列
例如我们生成长度为 139,根序列号为 25 的 Zadoff-Chu 序列,并输出序列的离散复数点、绘制复平面散点图及模值:
seq = zadoffChuSeq(25, 139);
disp(seq);
figure;
scatter(real(seq), imag(seq), 'filled');
xlabel('Real Part');
ylabel('Imaginary Part');
title('Complex Plot of seq');figure;
plot(abs(seq));
xlabel('Sample Index');
ylabel('Magnitude');
title('Magnitude of seq');
仿真结果如下:
①、复数点
生成的输出序列的离散复数点如下:
1.0000 + 0.0000i0.4266 - 0.9044i-0.9693 + 0.2461i0.8789 - 0.4770i0.3004 + 0.9538i-0.3219 + 0.9468i0.1687 + 0.9857i0.9746 - 0.2241i-0.9875 - 0.1576i0.8323 - 0.5544i0.7788 + 0.6273i0.6869 + 0.7268i0.9837 - 0.1798i-0.6702 - 0.7421i0.7497 + 0.6618i-0.8679 + 0.4967i-0.9693 - 0.2461i-0.9936 + 0.1128i0.0339 + 0.9994i0.4670 - 0.8842i0.1240 + 0.9923i-0.9571 + 0.2896i-0.9997 + 0.0226i-0.6360 + 0.7717i0.9634 + 0.2679i-0.9571 - 0.2896i0.6869 - 0.7268i0.9959 + 0.0903i0.9908 - 0.1352i0.0790 - 0.9969i-0.6702 + 0.7421i0.2570 - 0.9664i0.9746 + 0.2241i0.8064 + 0.5914i0.9959 - 0.0903i-0.3643 - 0.9313i0.2131 + 0.9770i-0.9271 - 0.3748i-0.1464 - 0.9892i-0.2351 - 0.9720i-0.9936 - 0.1128i0.6184 + 0.7858i-0.8446 - 0.5354i0.6184 - 0.7858i0.9353 - 0.3538i0.5823 - 0.8130i-0.8895 - 0.4570i0.7190 + 0.6950i-0.9977 + 0.0678i-0.4469 - 0.8946i-0.4060 - 0.9139i-0.9977 - 0.0678i0.5450 + 0.8385i-0.7031 - 0.7111i0.8565 - 0.5162i0.9908 + 0.1352i0.9504 - 0.3112i-0.3219 - 0.9468i-0.1015 + 0.9948i-0.5638 - 0.8259i0.6533 - 0.7571i0.7788 - 0.6273i-0.0565 - 0.9984i-0.8446 + 0.5354i0.8064 - 0.5914i0.2570 + 0.9664i-0.5259 + 0.8506i-0.2351 + 0.9720i0.9353 + 0.3538i-0.6005 - 0.7996i0.9353 + 0.3538i-0.2351 + 0.9720i-0.5259 + 0.8506i0.2570 + 0.9664i0.8064 - 0.5914i-0.8446 + 0.5354i-0.0565 - 0.9984i0.7788 - 0.6273i0.6533 - 0.7571i-0.5638 - 0.8259i-0.1015 + 0.9948i-0.3219 - 0.9468i0.9504 - 0.3112i0.9908 + 0.1352i0.8565 - 0.5162i-0.7031 - 0.7111i0.5450 + 0.8385i-0.9977 - 0.0678i-0.4060 - 0.9139i-0.4469 - 0.8946i-0.9977 + 0.0678i0.7190 + 0.6950i-0.8895 - 0.4570i0.5823 - 0.8130i0.9353 - 0.3538i0.6184 - 0.7858i-0.8446 - 0.5354i0.6184 + 0.7858i-0.9936 - 0.1128i-0.2351 - 0.9720i-0.1464 - 0.9892i-0.9271 - 0.3748i0.2131 + 0.9770i-0.3643 - 0.9313i0.9959 - 0.0903i0.8064 + 0.5914i0.9746 + 0.2241i0.2570 - 0.9664i-0.6702 + 0.7421i0.0790 - 0.9969i0.9908 - 0.1352i0.9959 + 0.0903i0.6869 - 0.7268i-0.9571 - 0.2896i0.9634 + 0.2679i-0.6360 + 0.7717i-0.9997 + 0.0226i-0.9571 + 0.2896i0.1240 + 0.9923i0.4670 - 0.8842i0.0339 + 0.9994i-0.9936 + 0.1128i-0.9693 - 0.2461i-0.8679 + 0.4967i0.7497 + 0.6618i-0.6702 - 0.7421i0.9837 - 0.1798i0.6869 + 0.7268i0.7788 + 0.6273i0.8323 - 0.5544i-0.9875 - 0.1576i0.9746 - 0.2241i0.1687 + 0.9857i-0.3219 + 0.9468i0.3004 + 0.9538i0.8789 - 0.4770i-0.9693 + 0.2461i0.4266 - 0.9044i1.0000 - 0.0000i
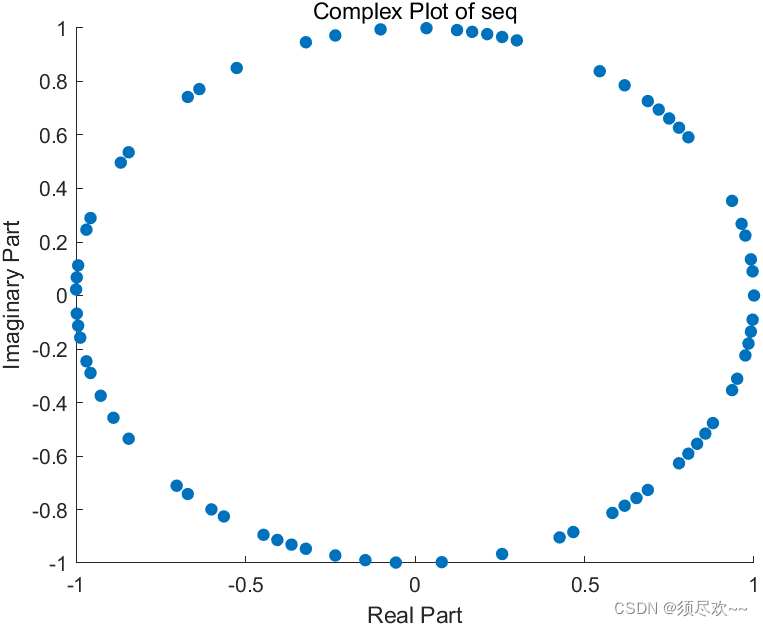
②、复平面散点图
对应的复平面上的散点图见下图,为单位圆:
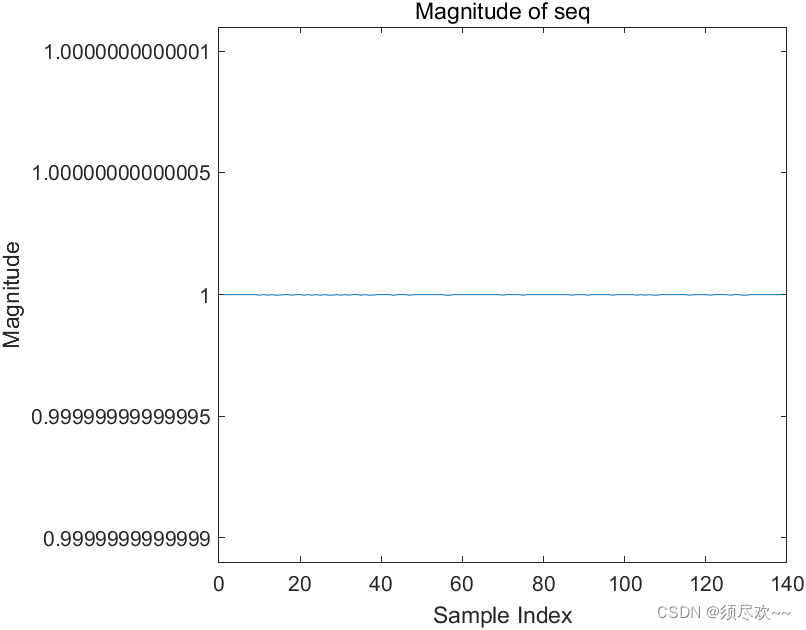
③、模值
对应的模值如下图,恒定为 1
2、ZC 序列循环移位
在对某一个 ZC 序列进行循环移位时,可使用 MATLAB 自带 circshift() 函数
语法:
Y = circshift(A,K)
Y = circshift(A,K,dim)
说明:
- Y = circshift(A,K) 循环将 A 中的元素平移 K 个位置。如果 K 为整数,则 circshift 沿大小不等于 1 的第一个 A 维度进行平移。如果 K 为整数向量,则每个 K 元素指示 A 的对应维度中的平移量。
- Y = circshift(A,K,dim) 循环将 A 中的值沿维度 dim 平移 K 个位置。输入 K 和 dim 必须为标量。
生成长度为 11,根序列号为 1 的 Zadoff-Chu 序列,循环移位长度为 3
Seq1 = zadoffChuSeq(1,11);
Seq2 = circshift(Seq1,3);
仿真运行时打断点可以看到原 Seq1 和移位后的 Seq2

3、ZC 序列自相关函数
我们还是使用上面生成长度为 139,根序列号为 25 的 Zadoff-Chu 序列,绘制 ZC 序列的自相关函数
seq = zadoffChuSeq(25,139);
[r,lags] = xcorr(seq);
plot(lags, abs(r));
xlabel('滞后索引');
ylabel('自相关');
title('ZC序列自相关');
仿真结果如下:
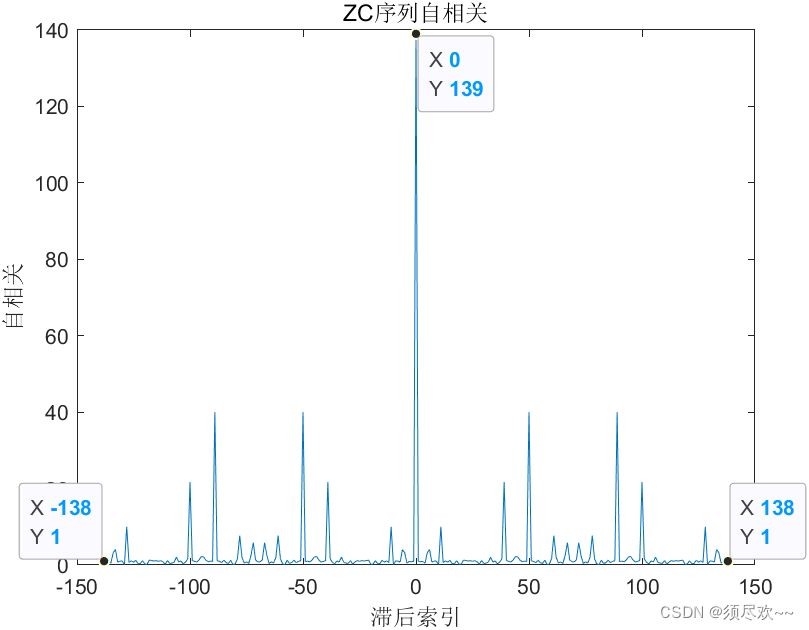
可以看到 ZC 序列具有集中的主瓣。
自相关的结果为 2N-1 个点,即 2 * 139 - 1 = 277 个点,关于 N=139 对称(这里从 -138 开始,因此关于 0 对称)。
有关 MATLAB 中自相关函数可以参考这个博客:一个例子学会自相关互相关的计算
4、ZC 序列循环自相关
seq1 = zadoffChuSeq(25,139);corr = fftshift(fft(seq1)) .* conj(fftshift(fft(seq1)));
subplot(2,1,1);
plot(abs(ifft(ifftshift(corr))));
xlabel('滞后索引');
ylabel('自相关');
title('ZC序列自相关');seq2 = circshift(seq1, 10); % 循环移位 10
corr = fftshift(fft(seq2)) .* conj(fftshift(fft(seq1)));
subplot(2,1,2);
plot(abs(ifft(ifftshift(corr))));
xlabel('滞后索引');
ylabel('循环自相关');
title('ZC序列循环自相关');
仿真结果如下:
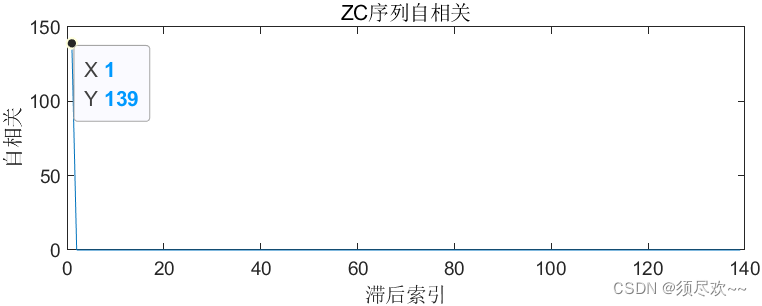
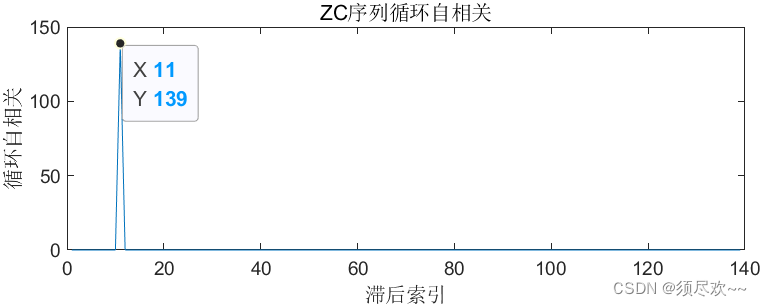
从仿真结果可以看出,ZC 序列具有良好的循环自相关特性且自相关峰值尖锐,对于任意 ZC 序列与其循环移位 a 位后的序列互不相关 a ≠ 0 a\neq 0 a=0;
从图中可以看到 ZC 序列循环移位后,原序列和移位后的相关峰值出现在移位大小的位置。
由此可得下面结论:
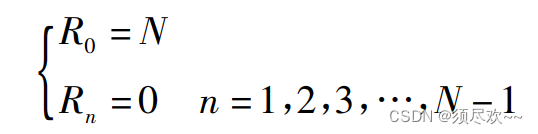
ZC 序列循环移位 N 后,原序列只与移位后的序列得良好的相关峰值且峰值在N处,其它位置的相关峰值为 0,这也是 preamble 检测的理论依据。
5、ZC 序列循环互相关
如果不同根产生的 ZC 序列进行相关运算会发生什么情况呢?下面我们构造两个根为 11 和 7 并且长度 N = 67 的 ZC 序列。
seq1 = zadoffChuSeq(11,67);
seq2 = zadoffChuSeq(7,67);corr = fftshift(fft(seq1)) .* conj(fftshift(fft(seq2)));
figure;
plot(abs(ifft(ifftshift(corr))));
xlabel('滞后索引');
ylabel('自相关');
title('ZC序列互相关');
两个不同根序列相关运算后的结果如下图:
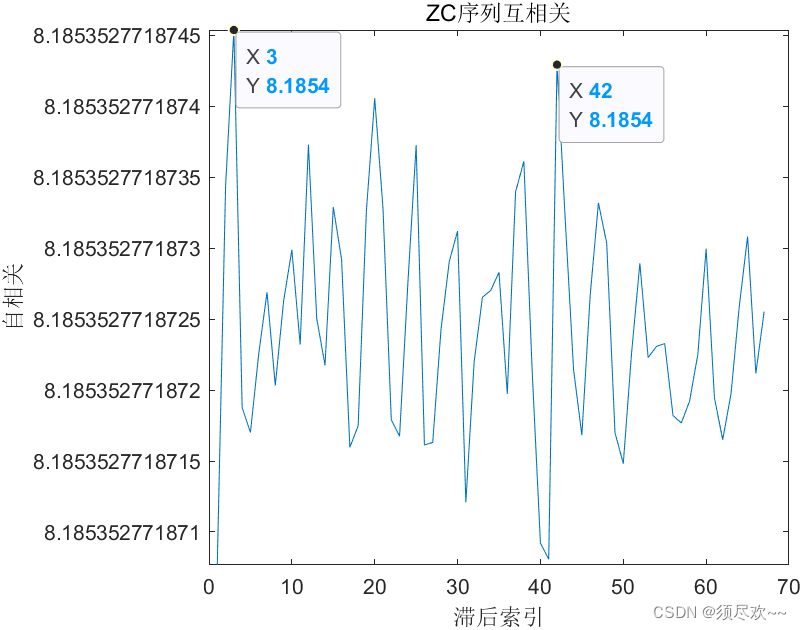
因此可得结论:若 N N N 与 ∣ u 1 − u 2 ∣ |u_1-u_2| ∣u1−u2∣ 互质,则互相关函数 ∣ R u 1 u 2 ∣ = N |R_{u_1u_2}|=\sqrt{N} ∣Ru1u2∣=N
我们从图上看出,对于不同根的序列再进行相关运算之后,不会产生像上面相同根的序列那样会产生又高又细的相关峰。
下面我们再构造两个根为 17 和 8 并且长度 N = 63 的 ZC 序列。
seq1 = zadoffChuSeq(17,63);
seq2 = zadoffChuSeq(8,63);corr = fftshift(fft(seq1)) .* conj(fftshift(fft(seq2)));
figure;
plot(abs(ifft(ifftshift(corr))));
xlabel('滞后索引');
ylabel('自相关');
title('ZC序列互相关');
两个不同根序列相关运算后的结果如下图:
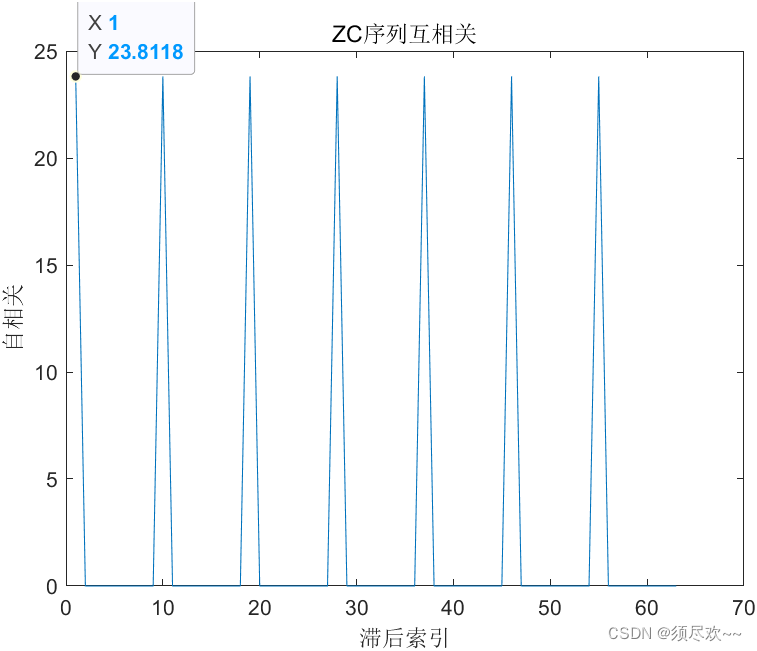
因此可得结论:若 N 为奇数,假设 N N N 与 ∣ u 1 − u 2 ∣ |u_1-u_2| ∣u1−u2∣ 有最大公约数 δ ≠ \delta \neq δ=,则互相关函数 ∣ R u 1 u 2 = δ N ∣ |R_{u_1u_2}=\sqrt{\delta N}| ∣Ru1u2=δN∣
∣ R u 1 u 2 ∣ = { δ N n = k δ 0 n ≠ k δ , k = 1 , 2 , . . . , N δ |R_{u_1u_2}|= \begin{cases} \sqrt{\delta N}& {n=k\delta}\\ 0& {n\neq k\delta} \end{cases},k=1,2,...,\frac{N}{\delta} ∣Ru1u2∣={δN0n=kδn=kδ,k=1,2,...,δN
上面我们说过:对相同长度的两个 ZC 序列,即一个序列的 root index 为 q 1 q_1 q1,另一个序列的 root index 为 q 2 q_2 q2,且 q 1 ≠ q 2 q_1\neq q_2 q1=q2,那么两个序列的归一化循环互相关值正好等于 1 / N z c 1/\sqrt{N_{zc}} 1/Nzc,这里一般假设 N z c N_{zc} Nzc 是质数,或者更一般地,认为 ∣ q 1 − q 2 ∣ |q_1-q_2| ∣q1−q2∣ 与 N z c N_{zc} Nzc 互质。
这里我们进行仿真证明一下:
tmp = [];
for i = 1: 10for j = (i+1) : 10if i < jSeqi = zadoffChuSeq(i,11); Seqj = zadoffChuSeq(j,11); cross_corr = abs(dot(Seqi, Seqj))/11;tmp = [tmp, cross_corr];endend
end
figure;
stem(tmp);
仿真图如下:
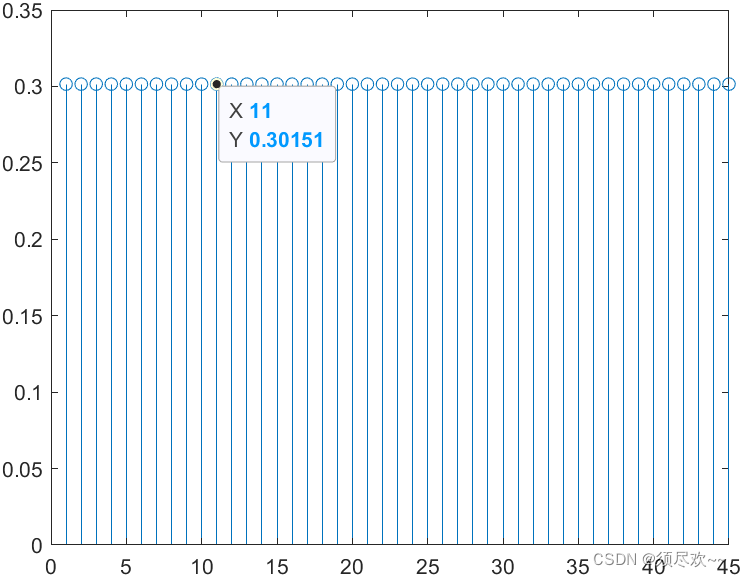
验证了我们上面所说的结论:两个序列的归一化循环互相关值正好等于 1 / N z c = 1 / 11 ≈ 0.3015 1/\sqrt{N_{zc}}=1/\sqrt{11}\approx0.3015 1/Nzc=1/11≈0.3015
6、ZC 序列傅里叶变换
这里介绍一下对 ZC 序列做完傅里叶变换后,再去分析复平面散点图及循环自相关特性
seq1 = zadoffChuSeq(25,139);
fft_seq1 = fft(seq1);figure;
scatter(real(fft_seq1), imag(fft_seq1));
xlabel('实部');
ylabel('虚部');
title('ZC序列fft后复平面表示');corr = fftshift(fft(fft_seq1)) .* conj(fftshift(fft(fft_seq1)));
figure;
plot(abs(ifft(ifftshift(corr))));
xlabel('滞后索引');
ylabel('循环自相关');
title('ZC序列fft后自相关');fft_seq2 = circshift(fft_seq1, 10); % 右移
corr = fftshift(fft(fft_seq2)) .* conj(fftshift(fft(fft_seq1)));
figure;
plot(abs(ifft(ifftshift(corr))));
xlabel('滞后索引');
ylabel('循环自相关');
title('ZC序列fft后循环自相关');
仿真结果如下:
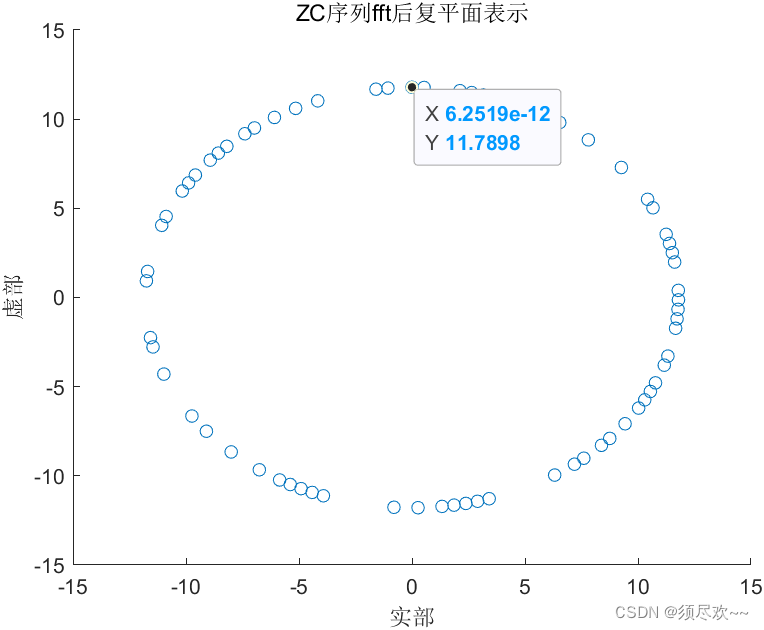
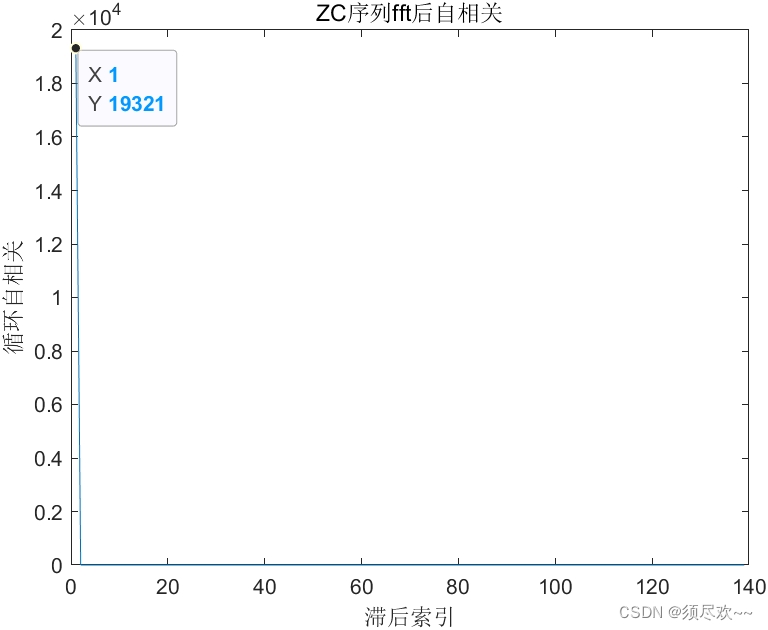
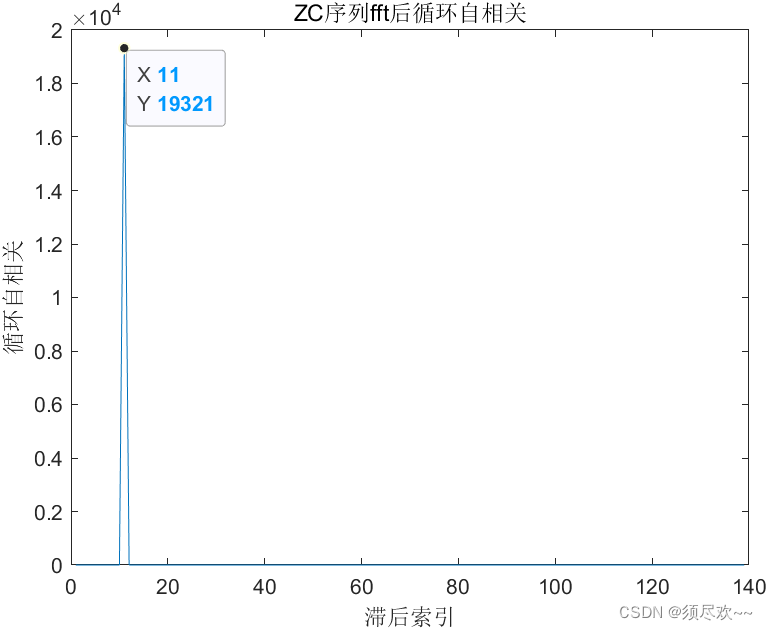
从上图仿真可以看出,结果显而易见,经过傅里叶变换之后的序列仍然具有同样的特性。
7、ZC 序列低峰均比特性
seq_lengths = 1:500:9999; % 不同的序列长度% 存储实部和虚部的峰均比值
real_part_PAPR_values = zeros(1, numel(seq_lengths));
imaginary_part_PAPR_values = zeros(1, numel(seq_lengths));for i = 1:numel(seq_lengths)seq1 = zadoffChuSeq(1, seq_lengths(i)); % 生成不同长度的ZC序列% 计算实部的峰值功率和均值功率real_part = real(seq1);real_part_peak_power = max(abs(real_part))^2;real_part_average_power = mean(abs(real_part))^2;% 计算虚部的峰值功率和均值功率imaginary_part = imag(seq1);imaginary_part_peak_power = max(abs(imaginary_part))^2;imaginary_part_average_power = mean(abs(imaginary_part))^2;% 计算实部和虚部的峰均比real_part_PAPR = 10 * log10(real_part_peak_power / real_part_average_power);imaginary_part_PAPR = 10 * log10(imaginary_part_peak_power / imaginary_part_average_power);real_part_PAPR_values(i) = real_part_PAPR; % 存储实部的峰均比值imaginary_part_PAPR_values(i) = imaginary_part_PAPR; % 存储虚部的峰均比值
end% 绘制实部峰均比图
subplot(2, 1, 1);
plot(seq_lengths, real_part_PAPR_values, '-o');
xlabel('序列长度');
ylabel('峰均比(dB)');
title('ZC序列实部峰均比');
grid on;% 绘制虚部峰均比图
subplot(2, 1, 2);
plot(seq_lengths, imaginary_part_PAPR_values, '-o');
xlabel('序列长度');
ylabel('峰均比(dB)');
title('ZC序列虚部峰均比');
grid on;
仿真结果如下:
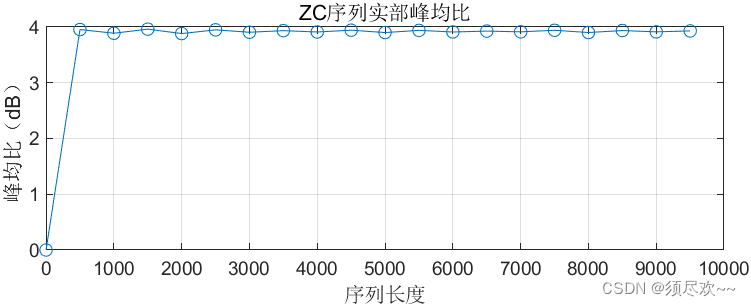
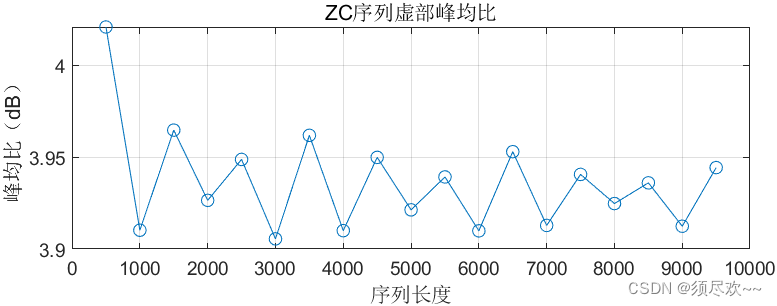
可以看到,ZC 序列峰均比较低,从而有利于射频功放信号发挥最大的效率。
参考文献:5GNR漫谈13:Zadoff –Chu(ZC)序列性质
我的qq:2442391036,欢迎交流!
这篇关于ZC序列理论学习及仿真的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








