本文主要是介绍DFT(离散傅里叶变换)的通俗理解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文包含了博主对离散傅里叶变换,负频率,实信号与复信号频谱的理解,如有不妥,欢迎各位批评指正与讨论。
文章目录
- DFT的理解
- 信号的频谱
- 实信号的频谱
- 复信号的频谱
DFT的理解
傅里叶变换是一种将信号从时域转换到频域的数学工具。它可以将一个号分解成不同频率的正弦和余弦波的叠加,从而更好地理解信号
的特性。
傅里叶变换公式:
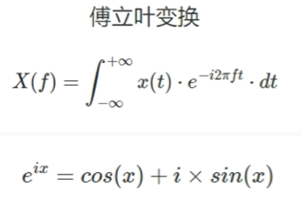
DFT计算公式:
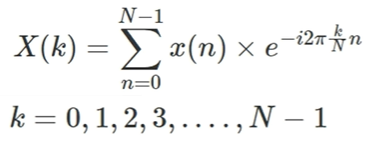
DFT的计算的理解:
离散傅里叶变换DFT的可视化讲解
DFT求出来的实部,虚部如何理解啦?
先说结论,实部代表cos序列的幅度,虚部代表sin序列的幅度。一个信号,按照傅里叶的说法,可以拆解成很多正弦波,或者说是由很多正弦波叠加到一起的。这些正弦波的幅度和频率之间的对应关系,就是信号的频域。
但是这里有个相位的问题,某个频率下有信号幅度,但是相位有可能是任意值,不同相位正弦波序列拼成的信号,完全不一样。
那样还需要一个相位和频率的关系图,不太好表示,如果这个频率没有信号,他的频率多少,没法弄。
后来想了个办法,我不去表示这个信号的相位了,我把这个信号在这个频率下的有相位的正弦信号拆解成两个正交的信号,不论信号是什么相位,都认为是一个零相位正弦信号和一个零相位余弦信号的叠加,我获得这个信号的正弦分量和余弦分量的幅度,就能反应这个信号。
这样就需要两个序列,一个正弦序列,一个余弦序列,他们两个正交,我们发现复数符合这个特点,正交,另外有那个宇宙最美公式欧拉公式加成,复数可以用指数表示,这个在数学上就变得很美很简单了,于是虚数就出现了,他表现的是信号的正弦分量。
参看:信号中的虚部的物理意义是什么?
可以理解为:傅里叶变换将信号在不同频率下进行cos和sin两个正交方向上的映射,得到两个分量,此两个分量的模构成了幅值,分量的角度构成了相位,由此包含了连续的不同频率成分下的幅值和相位信息,而DFT则是频率离散的看不同频率下的信息。得到的不同频率的实部虚部,可表示为信号是以该初始相位(以余弦为基准)开始的,该频率下以该幅值的圆进行旋转的信号的叠加。
信号的频谱
由傅里叶变换知道:实信号(实数信号,没有虚部)x(t)的傅里叶变换X(w)同时存在正负频率分量,且互为共轭;而复信号则只有单边频率分量。常用函数的傅里叶变换及其频谱。所以我们在MATLAB中使用fft函数进行傅里叶变换求得的频谱取模之后是具有对称性的。在进行fft求出的频谱后可以看的频谱从0-fs,可能会认为:根据Nyquist–Shannon(奈奎斯特-香农)采样定理,只能采集到fs/2的频率分量,所以高于fs/2的分量是没有意义的。实质上高于fs/2的频率分量是-fs/2到0的部分,这也是为什么我们一般会使用fftshift函数对求得的频谱做一个转换的原因MATLAB中fft与fftshift的区别。如前所述实信号的频率是共轭的,所以双边谱的幅值在非0处是单边谱的一半。这使得我们在查看信号的频谱时一般只关心正频率的部分,将双边谱的幅值大体乘2即转换为单边谱(注意我说的大体哦,做DFT的点数不同转换时有一点区别MATLAB中FFT频谱分析使用详解)。那是不是意味着频谱的负频率部分没有意义啦,又该如何理解负频率啦,接下来我们将在实信号和复信号的频谱小节中体现。
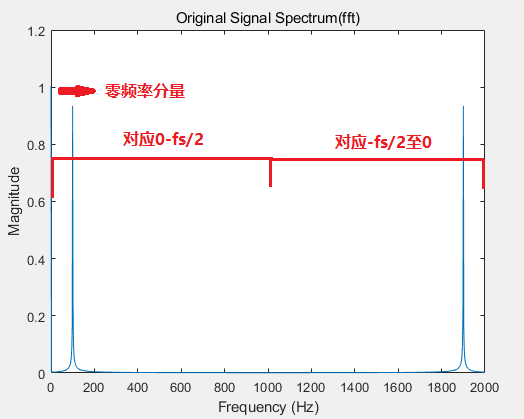
实信号的频谱
试想一下,信号的在圆上以相同的频率逆时针或顺时针旋转,得到的均为该频率分量的信号,在频谱上均需要表现出来。
逆时针旋转时:

顺时针旋转时:
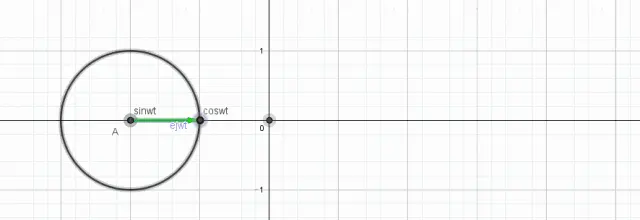
比较逆时针和顺时针,可以看到对余弦函数形态没有影响,因为余弦负角度等于它自身,正弦波形反相。
此时便出现了正频率和负频率的思想:逆时针旋转为正,顺时针旋转为负。
我们用数学公式来理解频谱:
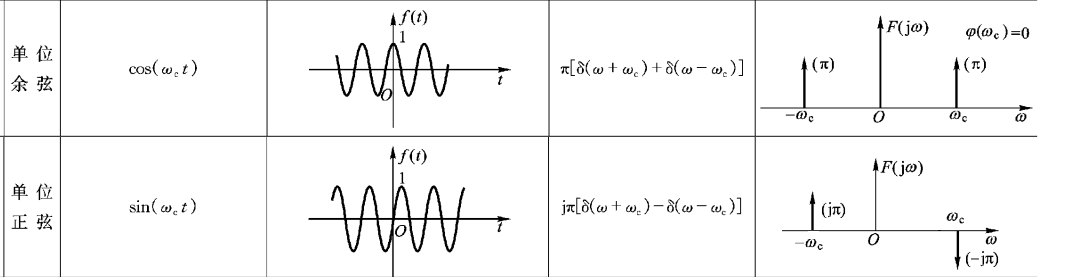
对于余弦 c o s ( w t ) = 0.5 ∗ c o s ( w t ) + 0.5 ∗ c o s ( ( − w ) ∗ t ) cos(wt)=0.5*cos(wt)+0.5*cos((-w)*t) cos(wt)=0.5∗cos(wt)+0.5∗cos((−w)∗t)
对于正弦 s i n ( w t ) = 0.5 ∗ c o s ( w t − π / 2 ) + 0.5 ∗ c o s ( ( − w ) ∗ t + π / 2 ) sin(wt)=0.5*cos(wt-\pi/2)+0.5*cos((-w)*t+\pi/2) sin(wt)=0.5∗cos(wt−π/2)+0.5∗cos((−w)∗t+π/2)

接下来对实信号频谱分析进行举例说明:
因为FFT/DFT是用余弦定义实部,正弦定义虚部。因此,FFT的0度,用作余弦波在正峰开始时的参考。
创建一个由频率为 15 Hz 和 40 Hz 的两个正弦波组成的信号。第一个波是相位为 −π/4 的正弦波,第二个波是相位为 π/2 的余弦波。以 100 Hz 的频率对信号进行 1 秒钟的采样。
标黄处说了,FFT/DFT以余弦为参考,则
s i n ( 2 ∗ π ∗ 15 ∗ t − π / 4 ) = s i n ( 2 ∗ π ∗ 15 ∗ t − π / 4 − π / 2 + π / 2 ) = c o s ( 2 ∗ π ∗ 15 ∗ t − π / 4 − π / 2 ) = c o s ( 2 ∗ π ∗ 15 ∗ t − 3 ∗ π / 4 ) sin(2*\pi*15*t-\pi/4)=sin(2*\pi*15*t-\pi/4-\pi/2+\pi/2)=cos(2*\pi*15*t-\pi/4-\pi/2)=cos(2*\pi*15*t-3*\pi/4) sin(2∗π∗15∗t−π/4)=sin(2∗π∗15∗t−π/4−π/2+π/2)=cos(2∗π∗15∗t−π/4−π/2)=cos(2∗π∗15∗t−3∗π/4)
即第一个波是相位为 −3π/4 的余弦波,第二个波是相位为 π/2 的余弦波。
clear all;close all;clc; %清理工作区,关闭所有窗口,清空文本
Fs = 100;
t = 0:1/Fs:1-1/Fs;
x = sin(2*pi*15*t - pi/4) + cos(2*pi*40*t + pi/2);
N = 100;
%计算信号的傅里叶变换。将变换幅值绘制为频率函数。
y = fft(x,N);
z = fftshift(y)/N;
figure(1);
ly = length(y);
f = (-ly/2:ly/2-1)*Fs/ly;
stem(f,abs(z))
title("Double-Sided Amplitude Spectrum of x(t)")
xlabel("Frequency (Hz)")
ylabel("|y|")
grid
%计算变换的相位,删除小幅值变换值。将相位绘制为频率函数。
tol = 1e-6;
z(abs(z) < tol) = 0;%删除小幅值变换值
theta = angle(z);
figure(2);
stem(f,theta/pi)
title("Phase Spectrum of x(t)")
xlabel("Frequency (Hz)")
ylabel("Phase/\pi")
grid
得到幅频和相频:
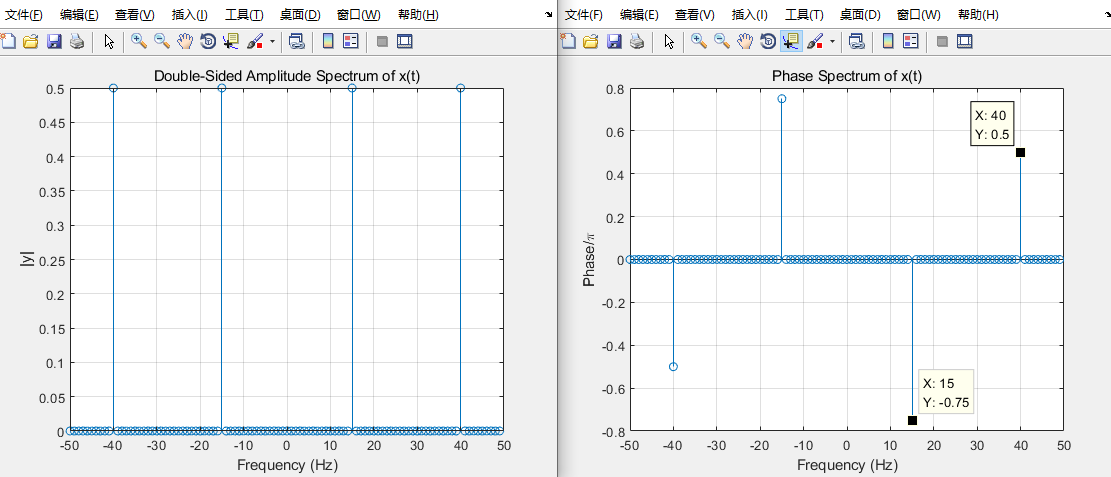
我们在工作区中查看经过fftshift并删除了小幅值的z的值,可以看到11、36、66和91位中有值。对应的是信号频率为-40Hz、-15Hz、15Hz和40Hz处的复数值。

对应欧拉公式的几何意义:
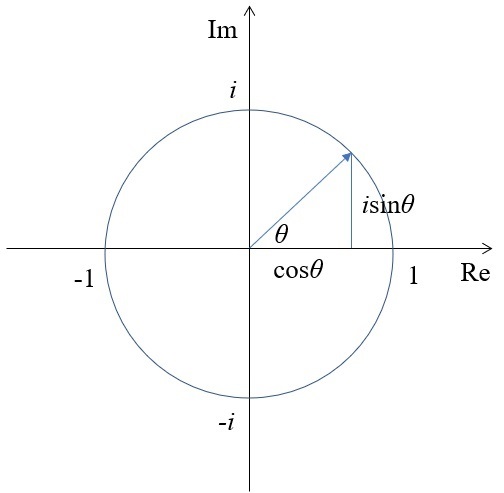
即(-0.3536,0.3536)即表示幅值为0.5,相位为 −3π/4的信号,依次类推。
我们用幅值和相位合成对于频率的信号:
15Hz:
0.5 ∗ c o s ( 2 ∗ p i ∗ 15 ∗ t − 3 ∗ π / 4 ) + 0.5 c o s ∗ ( 2 ∗ π ∗ ( − 15 ) ∗ t + 3 ∗ π / 4 ) = c o s ( 2 ∗ π ∗ 15 ∗ t − 3 ∗ π / 4 ) 0.5*cos(2*pi*15*t-3*\pi/4)+0.5cos*(2*\pi*(-15)*t+3*\pi/4)=cos(2*\pi*15*t-3*\pi/4) 0.5∗cos(2∗pi∗15∗t−3∗π/4)+0.5cos∗(2∗π∗(−15)∗t+3∗π/4)=cos(2∗π∗15∗t−3∗π/4)
40Hz:
0.5 ∗ c o s ( 2 ∗ p i ∗ 40 ∗ t + π / 2 ) + 0.5 ∗ c o s ( 2 ∗ p i ∗ ( − 40 ) ∗ t − π / 2 ) = c o s ( 2 ∗ π ∗ 40 ∗ t + π / 2 ) 0.5*cos(2*pi*40*t+\pi/2)+0.5*cos(2*pi*(-40)*t-\pi/2)=cos(2*\pi*40*t + \pi/2) 0.5∗cos(2∗pi∗40∗t+π/2)+0.5∗cos(2∗pi∗(−40)∗t−π/2)=cos(2∗π∗40∗t+π/2)
由此得到信号1是一个幅值为1,相位为 − 3 π / 4 -3\pi/4 −3π/4的信号;信号2是一个幅值为1,相位为 π / 2 \pi/2 π/2的信号。
参考:
FFT分析的负频率是什么?
如何正确理解信号处理中的负频率
一文读懂“为什么FFT有负频率”
复信号的频谱
而复信号则只有单边频率分量。
举例:频率为128或-128,相位为 π / 4 \pi/4 π/4的复数信号频谱
clear all;close all;clc; %清理工作区,关闭所有窗口,清空文本
N=1024;
fs=1024; %采样间隔为1/1000
t=(0:1023)/fs; %时间轴,注意要从0开始;若从1开始会以第一个点开始的位置计算,即pi/4+f0/fs*1*2pi=pi/2
f0=128; %复数频率
y=exp(i*(2*pi*f0*t+pi/4));
f_shift = (-N/2:N/2-1)*fs/N;
fft_y=fft(y,N)/N; %FFT
fft_shift = fftshift(fft_y);
plot(f_shift,abs(fft_shift));
title("复数信号频谱");
xlabel('f');
ylabel('y');
grid on;
频谱图:
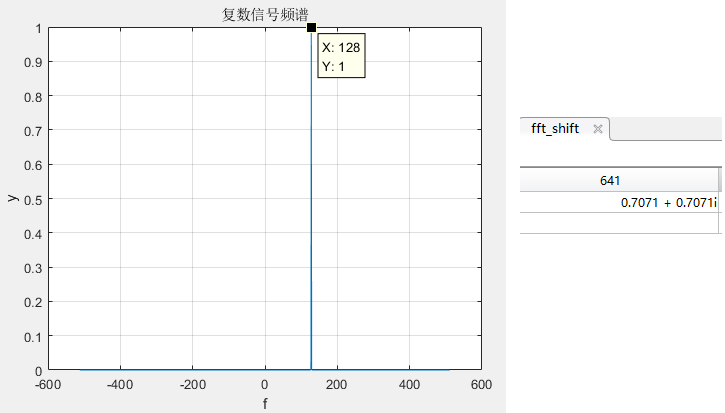
将f改为-128时频谱:
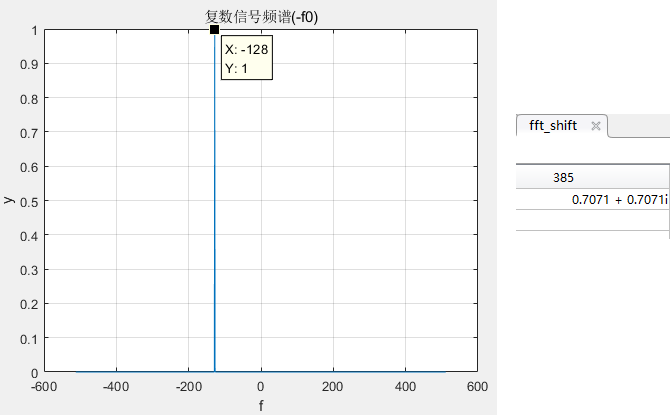
可以看出,当频率为正时,得到的频谱出现在正频率处;当频率为负时,得到的频谱出现在负频率处,且幅值为原信号的幅值。
这篇关于DFT(离散傅里叶变换)的通俗理解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





