研习代码 day48 | 动态规划——终极子序列问题（编辑距离）

本文主要是介绍研习代码 day48 | 动态规划——终极子序列问题（编辑距离），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、两个字符串的删除操作

        1.1 题目

        给定两个单词 word1 和 word2 ，返回使得 word1 和  word2 相同所需的最小步数。

        每步 可以删除任意一个字符串中的一个字符。

示例 1：

输入: word1 = "sea", word2 = "eat"
输出: 2
解释: 第一步将 "sea" 变为 "ea" ，第二步将 "eat "变为 "ea"

示例  2:

输入：word1 = "leetcode", word2 = "etco"
输出：4

提示：

• 1 <= word1.length, word2.length <= 500
• word1 和 word2 只包含小写英文字母

        1.2 题目链接

        583.两个字符串的删除操作

        1.3 解题过程和过程想法

        （1）解题过程

        通过最长公共子序列求最少的删除操作：先求出最长公共子序列，再用两串的总长度-2*最长公共子序列长度，即得到最少需删除操作的次数
        分析：当前的匹配情况会受到之前元素的情况所影响，且影响的方式是类似的，考虑采用动态规划的策略。
        # 数组：以i-1为结尾的word1字符串与以j-1为结尾的word2中最长公共子序列长度为dp[i][j]
        # 递推关系：若二者元素相匹配，当前情况取决于 用或不用 当前的元素，
                                  dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
                             若二者元素不匹配，当前情况的结果与不用当前元素的情况相同
                                  dp[i][j] = dp[i-1][j]

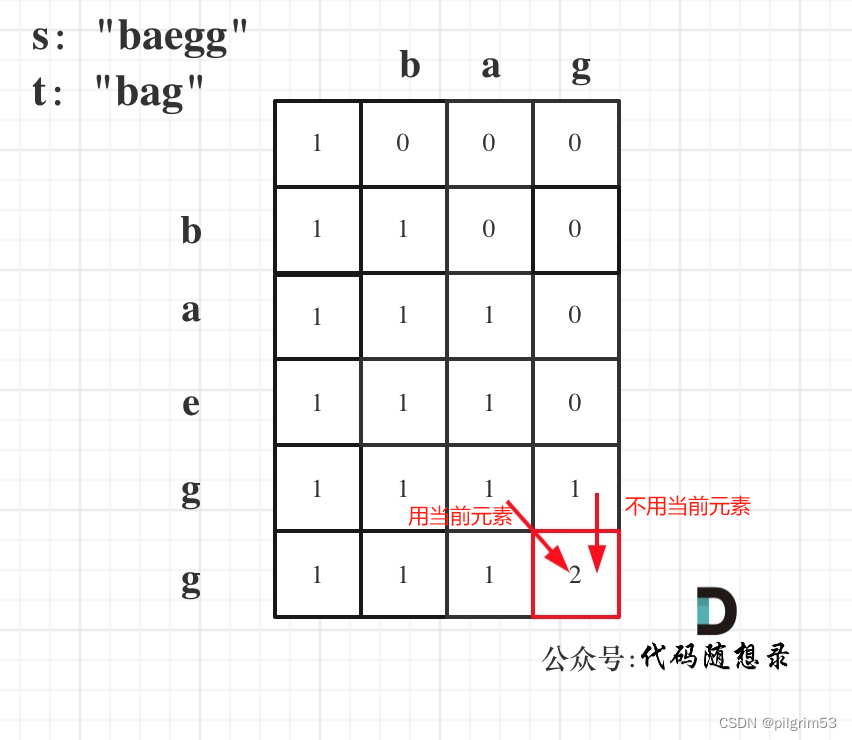
图片来源：代码随想录，红色文字是自己加的

        # 初始化：由上述递推关系可知当前位置的填写是基于左上方和正上方的元素，所以需要提前对首行首列进行初始赋值
                                dp[0][j] = 0         # 首行：没有母串，直接赋值 0
                                dp[i][0] = 1         # 首列：没有子串，即空子串，赋值1

        直接迭代当前最少的删除操作：
        当前的匹配情况会受到之前元素的情况所影响，且影响的方式是类似的，考虑采用动态规划的策略。
        # 数组：以i-1为结尾的word1字符串与以j-1为结尾的word2中最少需删除的长度为dp[i][j]
                dp = [[0]*(n+1) for _ in range(m+1)]

        # 递推关系：若两指针所指元素相同,更新当前数组值不需删除,即不更新 dp[i][j] = dp[i-1][j-1]
                             否则更新当前位置 dp[i][j] = min(dp[i-1][j]+1,dp[i][j-1],dp[i-1][j-1]+2)
注：不等时有三种情况——删第一个串中的元素，删第二个串中的元素，同时删除两个串中的元素
        # 初始化：因为当前位置的值由左上、正上方、左方推导，所以初始化首行首列
                            dp[0][j] = j    # 其中一个是空串，另一个串长度为 j 时，需删 j 个位置
                            dp[i][0] = i    # 其中一个是空串，另一个串长度为 i 时，需删 i 个位置

        （2）过程想法

        由于第一次做此类题目，第一种解法最先想到，后者是现学的

        1.4 代码

        1.4.1 通过最长公共子序列求最少的删除操作

class Solution:def minDistance(self, word1: str, word2: str) -> int:m = len(word1)n = len(word2)# 数组：以i-1为结尾的word1字符串与以j-1为结尾的word2中最长公共子序列长度为dp[i][j]dp = [[0]*(n+1) for _ in range(m+1)]# 递推关系：因为判断的不一定是连续的情况，直接迭代，dp[i][j] = dp[i-1][j-1] + 1for i in range(1,m+1):for j in range(1,n+1):if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1] + 1else:dp[i][j] = max(dp[i-1][j], dp[i][j-1])return m+n-2*dp[m][n]

        1.4.2 直接迭代当前最少的删除操作

class Solution:def minDistance(self, word1: str, word2: str) -> int:m = len(word1)n = len(word2)# 数组：以i-1为结尾的word1字符串与以j-1为结尾的word2中最少需删除的长度为dp[i][j]dp = [[0]*(n+1) for _ in range(m+1)]# 递推关系：若两指针所指元素相同，更新当前数组值不需要删除，即不更新 dp[i][j] = dp[i-1][j-1]；# 否则更新当前位置 dp[i][j] = min(dp[i-1][j]+1,dp[i][j-1],dp[i-1][j-1]+2)# 初始化：因为当前位置的值由左上、正上方、左方推导，所以初始化首行首列for j in range(n+1):dp[0][j] = j    # 其中一个是空串，另一个串长度为 j 时，需删 j 个位置for i in range(m+1):dp[i][0] = i    # 其中一个是空串，另一个串长度为 i 时，需删 i 个位置for i in range(1,m+1):for j in range(1,n+1):if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1]else:# 不等时有三种情况：删第一个串中的元素，删第二个串中的元素，同时删除两个串中的元素dp[i][j] = min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+2)return dp[m][n]

二、编辑距离

        2.1 题目

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数  。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

提示：

• 0 <= word1.length, word2.length <= 500
• word1 和 word2 由小写英文字母组成

        2.2 题目链接

        72.编辑距离

        2.3 解题过程和过程想法

        （1）解题过程        

        分析：当前的匹配情况会受到之前元素的情况所影响，且影响的方式是类似的，考虑采用动态规划的策略。
        # 数组：以i-1为结尾的word1字符串与以j-1为结尾的word2中最少需操作的次数为dp[i][j]
                dp = [[0]*(n+1) for _ in range(m+1)]

        # 递推关系：若两指针所指元素相同,更新当前数组值不需操作,即不更新 dp[i][j] = dp[i-1][j-1]
                             否则更新当前位置 dp[i][j] = min(dp[i-1][j]+1, dp[i][j-1]+1, dp[i-1][j-1]+1)
               注：不等时有三种操作：删长串中的元素，增加短串中的元素，替换一个串中的元素
        # 初始化：因为当前位置的值由左上、正上方、左方推导，所以初始化首行首列
                            dp[0][j] = j    # 其中一个是空串，另一个串长度为 j 时，需操作 j 个位置
                            dp[i][0] = i    # 其中一个是空串，另一个串长度为 i 时，需操作 i 个位置

        （2）过程想法

        解题思路与上一题类似，只是可操作的细节略有不同

        2.4 代码

class Solution:def minDistance(self, word1: str, word2: str) -> int:m = len(word1)n = len(word2)# 数组：以i-1为结尾的word1字符串与以j-1为结尾的word2中最少需操作的次数为dp[i][j]dp = [[0]*(n+1) for _ in range(m+1)]# 递推关系：若两指针所指元素相同，更新当前数组值不需要操作，即不更新 dp[i][j] = dp[i-1][j-1]；# 否则更新当前位置 dp[i][j] = min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+1)# 初始化：因为当前位置的值由左上、正上方、左方推导，所以初始化首行首列for j in range(n+1):dp[0][j] = j    # 其中一个是空串，另一个串长度为 j 时，需操作 j 个位置for i in range(m+1):dp[i][0] = i    # 其中一个是空串，另一个串长度为 i 时，需操作 i 个位置for i in range(1,m+1):for j in range(1,n+1):if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1]else:# 不等时有三种操作：删长串中的元素，增加短串中的元素，同替换一个串中的元素dp[i][j] = min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+1)return dp[m][n]

这篇关于研习代码 day48 | 动态规划——终极子序列问题（编辑距离）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---