机器学习：Leaning without Forgetting -- 增量学习中的抑制遗忘

本文主要是介绍机器学习：Leaning without Forgetting -- 增量学习中的抑制遗忘，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

传统的机器学习中，训练数据的类别都是固定的，这里也有一个假设，就是测试集也是类别固定的，这也是为什么现在很多模型在人类看来非常白痴的原因，套用一句非常经典的话来说，就是对于一个只见过猫狗的模型来说，那么这个世界在这个模型眼里里，只有猫狗两种可能。

所以很多研究人员开始探索增量学习这种技术，这种技术是模拟人的认知过程的，虽然我们无法见过这世界所有的东西，但是随着我见过的物体种类越来越多，那我们能够认识的事物也会越来越多，这是一个很美妙的构想。

但是，这个构想面临一个问题，虽然我们动不动就号称 AI, 或者人工智能，但是目前的 AI 和人脑的感知还是有很多的差别的，现在的 AI 还是建立在数学的基础上，利用矩阵，概率，优化来进行建模，不管怎么吹，都离不开数学的限制。增量学习中，最大的困难就是如何抑制遗忘，也就是说，模型不能学了新的事物，而遗忘了原来学过的事物。

我们都知道，神经网络可以看成是一个非常复杂的非线性系统，从数学角度来看，也就是把一个高维的向量（一般是图像） $\mathbf{x}$ 映射到一个低维的标签向量 $\mathbf{y}$ 上，如下所示：

$\mathbf{y} = \mathcal{T}(\mathbf{\Theta}, \mathbf{x})$

$\mathcal{T}$ 表示网络的结构， $\mathbf{\Theta}$ 表示网络中的参数，很显然， $\mathbf{\Theta}$ 是根据训练数据对 $\mathbf{x}, \mathbf{y})$ 通过优化方法，比如SGD 等优化得到的。不同的训练数据，将会得到不同的参数 $\mathbf{\Theta}$ 。

这就是我们所要面临的问题，原有类别的训练数据，通过训练可以得到参数 $\mathbf{\Theta}_o$ ，如果有了新的类别，那么这些新类别的训练数据会得到另外一组参数 $\mathbf{\Theta}_n$ ，而这组参数，只会对新类别的数据给出正确的响应，而原来类别的数据，已经无法正确区分了，这就好比狗熊掰棒子，永远只能记住当下，过往的数据，都给遗忘了。

这其实是数学优化本身的问题，机器学习，本质上还是一个数据拟合的问题，模型的参数，肯定是尽可能拟合当前的数据，因为模型本身是没有什么 “记忆功能” 的，你给我什么数据，我就拟合什么数据，没毛病。

所以为了让模型能有一定的 “记忆功能”，研究人员提出了很多不同的策略：

joint training 这大概是最直观的一种策略，既然模型只会拟合数据，那为了让模型能够记住，最直接的办法，就是把所有见过的数据都存起来，然后一块训练，这种策略大概是最简单的，但是却很笨重，效率很低，要耗费大量的存储以及计算资源。
duplicating and fine tuning 这种策略，简单来说，就是把模型复制一下，然后用复制的模型去拟合新的数据，原来的模型也不会受到影响，但是这种策略，也要耗费很多存储与计算资源，效率同样很低。
feature extraction 这种策略，简单来说，就是固定原来模型的 CNN 层，把 CNN 层当做一个特征提取器，然后去训练新的 FC 分类器，这种策略，由于没有去训练 CNN 层，优点是训练比较高效，缺点是可能泛化能力不足。
learning without forgetting 这就是今天我们要讲的重点，这是 ECCV 2016 的一篇文章，思路很简单，却很巧妙。下面重点介绍一下这种技术。

下面的图（来自参考文献中的示意图），简单示意了几种不同的抑制遗忘的训练策略：

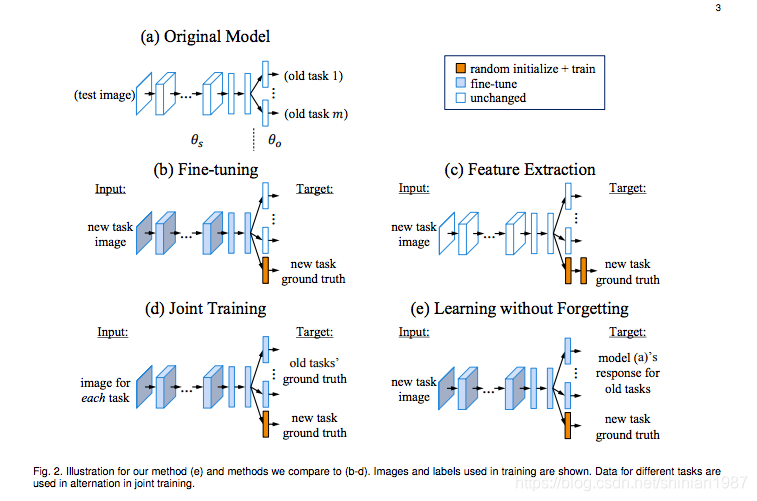
learning without forgetting

我们已经讨论过，模型的记忆功能其实就体现在参数的值上，要想让模型有“记忆功能”，模型的参数就不能有太大的变化，模型在拟合新数据的时候，参数肯定是会发生变化的，要想让参数记住原来的数据，直观的方法就是混入原来的数据一块训练，但是如果没有原来的数据怎么办呢，文章的作者就提出了一种类似 “伪标签” 的策略，既然我只是要模型也要见到原来数据分布，那我完全可以用旧模型先在部分新数据上打上标签，然后训练的时候，这部分打上“伪标签”的训练数据可以看成是原来的数据，和剩下的新数据一块投入训练，这就是 learning without forgetting 的关键思路。

这个思路很简单，却很巧妙，也很有效，既避免了存储太多的旧数据，又能够让模型不会只拟合新数据而造成遗忘问题。模型训练的 loss 也很简单：

$\mathcal{L}_{new} = \mathbf{y}_n \cdot log(\mathbf{p}_n)$

$\mathbf{y}_n$ 表示新数据的真实标签， $\mathbf{p}_n$ 表示新数据在模型上的输出概率。

$\mathcal{L}_{old} = \bar {\mathbf{y}}_o \cdot log(\bar{\mathbf{p}}_o)$

$\bar {\mathbf{y}}_o$ 表示新数据的旧模型上的“伪标签”， $\bar{\mathbf{p}}_o$ 表示新数据在模型上的输出概率。

作者也利用了蒸馏的策略，来优化 $\bar {\mathbf{y}}_o$ ， $\bar{\mathbf{p}}_o$

$\bar{y}_{o}^{(i)} = \frac{ (\bar{y}_{o}^{(i)})^{1/T} }{ \sum_{j} (\bar{y}_{o}^{(j)})^{1/T} } , \quad \bar{p}_{o}^{(i)} = \frac{ (\bar{p}_{o}^{(i)})^{1/T} }{ \sum_{j} (\bar{p}_{o}^{(j)})^{1/T} }$