＜论文阅读＞ CorAl – 点云是否正确对齐？ CorAl – Are the point clouds Correctly Aligned?

【摘要】：在机器人感知中，许多任务依赖于点云配准。然而，目前还没有一种方法可以在没有特定环境参数的情况下可靠地自动检测错位点云。我们提出"CorAl"，一种用于点云对的对齐质量度量和对齐分类器，它有助于评估配准性能的能力。 CorAl 比较了两个点云的联合熵和分离熵。分离熵提供了可以认为是环境固有的熵的度量。因此，如果点云正确对齐，则联合熵应明显更低。计算期望熵使得该方法对小的对齐误差也很敏感，这些误差特别难以检测，并且适用于一系列不同的环境。我们发现 CorAl 能够以 95% 的准确率在以前看不见的环境中检测到小的对齐错误，并在以前的方法中实现了实质性的改进。

一、引言

  为了创建安全高效的移动机器人，需要内省和可靠性感知能力来评估感知故障并从故障中恢复。许多感知任务，包括定位、场景理解和传感器校准，都依赖于点云配准。然而，由于配准成本函数的局部最小值、未补偿的运动失真 、噪声或配准问题在几何上受到约束 ，配准可能会提供不正确的估计。因此，必须测量对齐质量并在质量低时拒绝重新评估对齐。在过去，已经提出了大量的方法来评估点云对的对齐质量。这些指标通常可用于测量配准过程中的相对对齐误差，但在执行配准后关于点云是否正确对齐只能提供有限的信息 。直到今天，很少有研究针对配准后对齐正确性的测量，根据以前的工作报告，当应用于从新环境获取的点云时，基于 AdaBoost 和 NDT 评分函数的对齐正确性分类会降低。
  在本文中，我们提出了"CorAl"(Correctly Aligned)：一种内省测量和检测先前陪准的点云对之间未对齐的方法。CorAl 专门用于弥合在应用于新的看不见的环境时分类性能的差距。
  我们的方法以信息论为基础，并提供了直观的对齐正确性度量。 CorAl 测量联合和分离点云中的平均微分熵之间的差异。对于对齐良好的点云，联合点云和分离的点云具有相似的熵。相反，未对齐的点云往往会“模糊”场景，这可以通过联合熵的增加来衡量，如图 3 所示。通过使用分离的点云来估计场景中固有的熵，我们提出的方法可以评估一系列不同环境中的质量。

  本文的贡献是对点云对之间的对齐正确性的直观和简单的度量。我们演示了如何使用这种质量度量来训练简单的模型来检测点云之间较小的对齐误差，本文不考虑大的误差。为了训练我们的模型，我们使用以前校正过的扫描，假设没有对齐错误。
  我们提出以下主张：

• (i) 我们提出的方法 CorAl 通过考虑预期场景熵来测量点云对齐的正确性。
• (ii) 我们的方法在广泛的环境中是准确的，并且可以很好地推广到新环境而无需重新训练

二、相关工作

  文献中已经使用了几种方法来评估对齐质量。然而，在大多数情况下，这些方法都是以特别的方式使用的。很少有系统评估它们作为分类器检测对齐点云与未对齐点云的通用能力。
  一种常用的对齐度量是均方根 (RMS) 点到点距离，通过异常值阈值截断。这也是通过迭代最近点匹配最小化函数。然而，该措施已被证明对环境和异常值阈值的选择高度敏感。因此，对于对齐正确性分类来说，这是一个很差的衡量标准。
  相反，一组方法试图以协方差矩阵的形式估计点云对之间的对齐不确定性。有些人使用蒙特卡罗策略通过对区域中的配准进行抽样来估计不确定性。这种彻底的搜索在移动机器人中是不切实际的。其他人尝试使用 Hessian 来估计封闭形式的不确定性，表示对齐得分函数在最小值附近的陡度。这些方法假设配准已达到全局最大值，这不一定是正确的。直到今天，与匹配分数相比，基于不确定性协方差的对齐分类还不够准确。
  等等…
据我们所知，没有一种方法可以准确地执行点云对齐分类，并且无需参数调整或重新训练即可很好地应用到新环境。

三、CORAL 法

  我们的工作受到 Droeschel 和 Behnke 提出的用于地图质量评估的平均地图熵 (MME) 度量的启发。 MME 基于微分熵并测量多元高斯分布的随机性。 Droeschel 和 Behnke 在评估地图细化时使用了 MME，因为没有准确的地面实况。正如我们的评估所示，MME 不能用作通用的对齐质量度量，因为它还受到测量噪声、样本密度和环境几何形状的影响。与 CorAl 相比，MME 受环境变化的影响更大。因此，预计该测量不会在例如结构化仓库和非结构化户外森林环境之间进行推广。我们使用双熵计算测量来克服这种影响：

1. 分别在两个点云中计算
2. 在联合点云中计算

我们认为连接两个对齐良好的点云不应该引入额外的不确定性。如果点云充分重叠，熵应该保持不变。

A.计算联合和分离熵

  我们的方法对密集点云 ${\mathcal{P}}_a$, ${\mathcal{P}}_b$ 进行操作，给定一个共同的固定世界坐标系，其中包含笛卡尔空间中的一组点$p_k=[xyz]$。为了以后使用，我们定义联合点云 ${\mathcal{P}}_j={\mathcal{P}}_a\cup {\mathcal{P}}_a$；即 ${\mathcal{P}}_a$和 ${\mathcal{P}}_b$ 中的所有点。
  从每个点$p_k$ 周围半径$r$内的所有点，我们计算样本协方差$\Sigma (p_k)$。根据样本协方差$det(\Sigma (p_k))$的行列式，我们可以计算微分熵为：
$$h_i(p_k)=\frac{1}{2}ln(2\pi edet(\Sigma (p_k))\text{\hspace{1em}(1)}$$

  对于包含$p_k$的点云$i=a,b$。根据等式一着色的点云示例见图a 和 b。${\mathcal{P}}_i$的微分熵之和计算为：
$$H_i({\mathcal{P}}_i)=\sum _{k-1}^{|{\mathcal{P}}_b|}{h}_i(p_k)\text{\hspace{1em}(2)}$$
其中$|{\mathcal{P}}_b|$是${\mathcal{P}}_b$中的点云数。
  使用公式二， 我们可以推导出两个点云的这些分离和联合平均微分熵的度量 ${\mathcal{P}}_a$, ${\mathcal{P}}_b$
$$H_{sep}=\frac{H_a({\mathcal{P}}_a)+H_b({\mathcal{P}}_b)}{|{\mathcal{P}}_a|+|{\mathcal{P}}_b|}\text{\hspace{1em}(3)}$$$$H_{joint}=\frac{H_j({\mathcal{P}}_j)}{|{\mathcal{P}}_j|}=\frac{H({\mathcal{P}}_a\cup {\mathcal{P}}_b)}{|{\mathcal{P}}_a|+|{\mathcal{P}}_b|}\text{\hspace{1em}(4)}$$
  我们的第一个对齐质量度量使用联合和分析的平均微分熵之间的差异：
$$Q({\mathcal{P}}_a,{\mathcal{P}}_b)=H_{joint}({\mathcal{P}}_j)-H_{sep}({\mathcal{P}}_a,{\mathcal{P}}_b)\text{\hspace{1em}(5)}$$
这也可以通过：
$$q_k(p_k)=h_j(p_k)-h_i(p_k)\text{\hspace{1em}(6)}$$
  其中点熵是在联合点云$j$上评估的，而分离的点云$i=(aorb)$来自$p_k$。根据等式六计算的点云熵差着色的点云示例如图所示c 和 d。

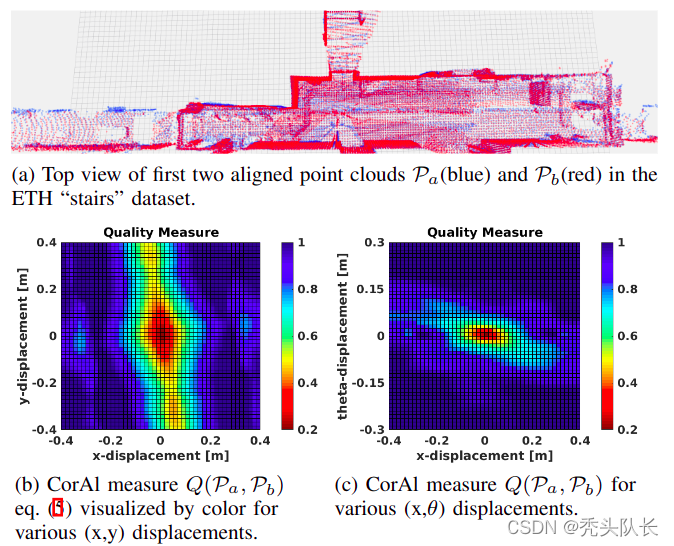
通常，对于对齐良好的点云，$Q({\mathcal{P}}_a,{\mathcal{P}}_b)$接近于零，并且随着对齐误差的增加而增加，如图所示，通过可视化了解正确对齐周围的位置和角度对齐误差。

  在结构化环境中获得的对齐良好的点云${\mathcal{P}}_a\cup {\mathcal{P}}_b$对于大多数点云$p_k$具有低微分熵。这反映在样本协方差的行列式的低值上。由于行列式可以表示为样本协方差$det(\Sigma (p_k))={\lambda }_1{\lambda }_2{\lambda }_3$的特征值的乘积，我们看到当较大的特征值恒定时，该度量对特征值的最低值的增加很敏感。例如，平面上点的熵表示为具有两个大 $({\lambda }_1,{\lambda }_2)$ 和一个小 $({\lambda }_3)$特征值的扁平化分布。错误的改变联合点云中的点分布从平面变为椭圆，可以观察到最小特征值${\lambda }_3$的增加，这使得测量对平面表面的错误对准敏感，但可以很好地推广到其他几何形状。如评估所示，该度量可以捕获点云之间的差异，无论这些差异是由于移动时扫描时可能发生的刚性错误匹配或扭曲造成的。例如，由于振动或传感器速度估计错误。这意味着当与不补偿运动失真或精度低的配准方法或里程计框架一起使用时，该方法可能过于敏感。
  点云之间需要重叠以产生对齐的证据。因此，我们将重叠小于 10% 的点云分类为未对齐。将与另一个邻居相距$r$的所有点云定义为重叠，非重叠点对等式五中的质量度量没有影响。

B. 动态半径选择和异常值剔除

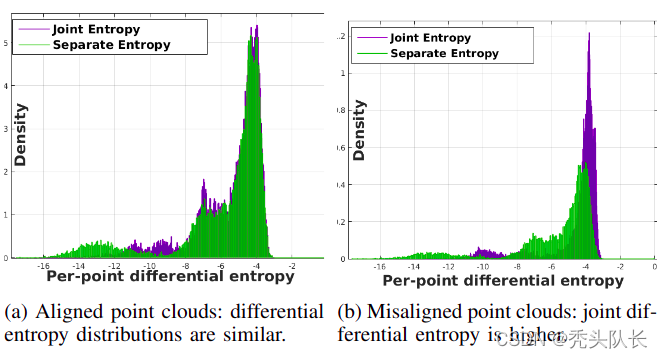
  对于对齐良好的点云，质量度量接近于零，这意味着联合点云和分离的点云具有相似的每个点熵的均值和概率分布，如图所示。

不幸的是，熵在等式一中，当行列式$det(\Sigma (p_k))$ 接近于零并且行列式的小幅增加导致熵的大幅增加时，是不合时宜的。因此，即使在连接良好对齐的点云时，最低测量熵也会增加（这表明未对齐），如上图所示。不合时宜的熵出现在点密度较低的地方，通常是孤立点或远离传感器的地方，其半径$r$不足以包含表示环境中几何形状的点。这种熵问题的影响可以通过最大化比率来减轻：$$Q_s=\frac{Q_{misaligned}({\mathcal{P}}_a,{\mathcal{P}}_b)}{Q_{aligned}({\mathcal{P}}_a,{\mathcal{P}}_b)}$$较大的比率表明该度量能够区分对齐和未对齐的点云。我们提出了三种策略来解决由于传感器采样密度的变化而导致的不合时宜的熵。

1. 修改为$h_i(p_k)=\frac{1}{2}ln(2\pi edet(\Sigma (p_k))+\epsilon )$，其中限制了可能的最低熵。这确保沿线和平面分布的点的熵相似。通过比较图a-b可以看出改进。
2. 根据点$p_k$和传感器位置之间的距离选择半径$r$，以适应点密度随距离增加而递减。因此选择半径为：$r=dsin(a)$，在$r_{min}<r<r_{max}$时，其中$\alpha$是传感器的垂直分辨率。对于其他传感器类型，例如RGB-D，同样可以根据角度传感分辨率来选择分辨率。动态半径使质量测量能够包括远离传感器的更多点，并正确检测这些点的对齐和未对齐，如图 c所示。
3. 删除 $E_{reject}$具有最低熵的点$p_k$的百分比。效果如图d。

C. 分类

我们使用逻辑回归作为分类模型：
$$p=\frac{1}{1+e^{-z}}z={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2\text{\hspace{1em}(7)}$$$$y_{pred}=\{\begin{array}{l}alignedifp\ge t_h\\ misalignedifp<t_h\end{array}\text{\hspace{1em}(8)}$$其中 $x1,x2$ 是输入变量（在章节中针对每个方法进行了描述）。$H_{sep}$和$H_{joint}$分别传递给$x_1=H_{joint},x_2=H_{sep}$，而不是通过质量测量$x_1=Q({\mathcal{P}}_a,{\mathcal{P}}_b)$，${\beta }_0,{\beta }_1,{\beta }_2$是学习模型参数，$p_i$是类别概率，$t_h$这是类别概率阈值，可以根据应用需要进行调整。例如，在移动机器人中，希望未对齐的点云不会被意外报告为对齐（误报），这可能导致系统故障。相反，归类为未对齐的对齐点云通常是无害的。因此，可以增加 $t_h$以拒绝误报，从而提高鲁棒性。我们使用默认的 $thresholdth=0.5$。

五、结论

  在本文中，我们介绍了 CorAl，这是一种有原则且直观的点云之间对齐正确性的度量。使用双熵测量将在分离的点云中发现的预期熵与实际熵进行比较，CorAl 可以测量点云对齐的正确性，并且在对公共数据集进行评估时大大优于以前的方法。具体来说，我们能够使用 CorAl 来训练基于逻辑回归的分类器，该分类器在各种环境中同时准确。我们的实验表明，我们的方法可以很好地从非结构化和半结构化环境到结构化环境，以及从结构化到半结构化环境。没有一种评估方法能很好地从结构化环境推广到非结构化环境。因此，我们得出结论，在训练数据足够多样化的情况下，可以训练出一个通用且准确的对齐分类器。在 livedata 上取得了相对适中的结果 96%。我们认为，低质量的地面实况（通过激光雷达里程计和人工检查获得）导致 CorAl 得分的高方差。该分数对小偏差很敏感，因此需要更高质量的基本事实来进行公平的评估。我们相信 CorAlper 点质量和分类可以成为对齐评估的有用工具，并且可以通过作为故障检测步骤来提高各种感知任务的鲁棒性。
  未来我们将研究如何自动学习传感器的特定参数或使用距离图像来寻找相邻点进行协方差计算。这可以解决由于不同传感器和环境尺度引起的点密度变化。

码字不易，转载请注明出处～