本文主要是介绍MIMO系统中基于K-Best的球形译码算法的matlab仿真,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、理论基础
二、核心程序
三、测试结果
一、理论基础
MIMO (Multiple-Input Multiple-Output) 系统是无线通信领域中的一种关键技术,它利用多个天线同时发送和接收数据,从而提高通信系统的容量和可靠性。在MIMO系统中,球形译码算法是一种有效的信号检测算法,它能够在高噪声环境下实现较高的误码率性能。基于K-Best的球形译码算法是球形译码的一种扩展,它通过考虑多个最优解来进一步提高性能。
基于K-Best的球形译码算法的核心思想是在球形译码的过程中,保留K个最可能的解,而不是只保留一个最可能的解。在每次迭代中,算法会计算每个解的路径度量,并保留路径度量最小的K个解。最后,从这K个解中选择一个路径度量最小的解作为最终解。
路径度量计算:
路径度量是评估解的质量的重要指标,它定义为:
PM(i) = (1/N) * ||y - Hx(i)||^2
其中,y是接收信号向量,H是信道矩阵,x(i)是第i个解,N是发送天线的数量。路径度量越小,解的质量越高。
K-Best解的选择:
在每次迭代中,选择路径度量最小的K个解作为候选解。这可以通过对所有解的路径度量进行排序,并选择前K个解来实现。
迭代过程:
在每次迭代中,对K个候选解进行扩展,并计算每个扩展解的路径度量。然后,选择路径度量最小的K个扩展解作为下一次迭代的候选解。迭代过程继续进行,直到找到满足终止条件的解。
基于K-Best的球形译码算法通过保留多个最优解来提高球形译码的性能。它通过计算路径度量和选择K个最优解来进行迭代搜索,直到找到满足终止条件的解。该算法在高噪声环境下具有较高的误码率性能,因此在实际无线通信系统中得到广泛应用。
空间调制技术因其具备更高的数据传输效率、更高的频谱效率和更低的功率损耗而受到学术界和工业界的广泛关注。空间调制技术通过控制发射天线的激活状态传输附加的比特信息,从而实现在不增加无线通信资源的前提下提高通信的效率。另一方面,正交频分复用技术作为4g通信系统的关键技术之一,被广泛应用到各种通信协议和场景中。不幸的是正交频分复用技术存在峰均比过高的问题。单载波系统可以很好地解决峰均比问题,将空间调制技术应用到单载波系统是一种可行的方案。
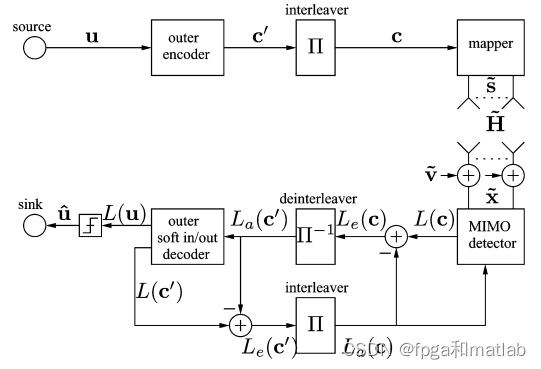
多输入多输出(MIMO)的(ML)性能侦查作为低复杂度MIMO解码算法KSE被证明适用于超大规模集成电路(VLSI)并且能够支持软输出。进一步提出了改进的KSE(MKSE)译码算法提高软输出KSE的性能修改。此外,还提出了一种VLSI体系结构,用于这两种算法。有几个低复杂性和低功耗所提出的算法和VLSI中包含的特征建筑学提出的硬输出KSE解码器和软输出MKSE解码器是在0.35μ以及0.13 m CMOS技术。已实施的硬输出KSE芯片芯为5.76mm2,具有91K栅极。这个KSE解码吞吐量高达53.3Mb/s,核心功率在100 MHz时钟频率和2.8 V下消耗626 mW供给所实现的软输出MKSE芯片可以实现解码吞吐量超过100 Mb/s,0.56 mm2核心区和97K门。实施结果表明实现接近ML的性能和高检测是可行的4 4 16-QAM MIMO系统的吞吐量算法和具有合理复杂性的VLSI结构.

二、核心程序
....................................................................
%设置调制方式
Mode_Type1 = 4;
Mode_Map1 = [-(Mode_Type1-1):2:Mode_Type1-1];Mode_Type2 = 16;
Mode_Map2 = [-(Mode_Type2-1):2:Mode_Type2-1];Mode_Type3 = 64;
Mode_Map3 = [-(Mode_Type3-1):2:Mode_Type3-1];Mode_Type4 = 256;
Mode_Map4 = [-(Mode_Type4-1):2:Mode_Type4-1];Sim_EbN0 = [0:5:25];
Ntant = 4;
Nrant = 4;
Bers = zeros(1,length(Sim_EbN0));
K = 16;%14,5,12
Tj = [2000,1000,500,500,400,200];for j = 1:length(Sim_EbN0)Eb_N0 = Sim_EbN0(j);sigma = 10^(-Eb_N0/20);Nerr = 0;Num = 0;%根据误码率判决门限进行误码率统计while Nerr <= Tj(j)Nerr%产生信道Nt = Ntant;Nr = Nrant;H(1:Nt ,1:Nr) = randn(Nt ,Nr);H(Nt+1:2*Nt,1:Nr) = randn(Nt ,Nr);H(1:Nt ,Nr+1:2*Nr) =-H(Nt+1:2*Nt,1:Nr);H(Nt+1:2*Nt,Nr+1:2*Nr) = H(1:Nt ,1:Nr); H = 1/sqrt(2)*H;%QR分解[Q,R] = qr(H);%产生噪声大小N = sigma*randn(Nr*2,1);SignalTx = [];for jj = 1:Ntant%发送信号%四个天线,四种调制方法SignalTx1 = Mode_Map1(unidrnd(Mode_Type1,2*Ntant/4,1))';%天线1SignalTx2 = Mode_Map2(unidrnd(Mode_Type2,2*Ntant/4,1))';%天线2SignalTx3 = Mode_Map3(unidrnd(Mode_Type3,2*Ntant/4,1))';%天线3SignalTx4 = Mode_Map4(unidrnd(Mode_Type4,2*Ntant/4,1))';%天线4if mod(Num,Ntant) == 0 SignalTx = [SignalTx;SignalTx1];endif mod(Num,Ntant) == 1 SignalTx = [SignalTx;SignalTx2];endif mod(Num,Ntant) == 2 SignalTx = [SignalTx;SignalTx3];endif mod(Num,Ntant) == 3 SignalTx = [SignalTx;SignalTx4];endend%最后发送的信号if mod(Num,Ntant) == 0 %接收信号SignalRx = H*SignalTx + N;%最终接收到的信号%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%NQ = Q'*N;RN = R*SignalTx+NQ;SignalRX_rec = func_KSE(R,RN,K,Mode_Map1,Mode_Type1);end%最后发送的信号if mod(Num,Ntant) == 1 %接收信号SignalRx = H*SignalTx + N;%最终接收到的信号%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%NQ = Q'*N;RN = R*SignalTx+NQ;SignalRX_rec = func_KSE(R,RN,K,Mode_Map2,Mode_Type2);end %最后发送的信号if mod(Num,Ntant) == 2 %接收信号SignalRx = H*SignalTx + N;%最终接收到的信号%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%NQ = Q'*N;RN = R*SignalTx+NQ;SignalRX_rec = func_KSE(R,RN,K,Mode_Map3,Mode_Type3);end%最后发送的信号if mod(Num,Ntant) == 3 %接收信号SignalRx = H*SignalTx + N;%最终接收到的信号%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%NQ = Q'*N;RN = R*SignalTx+NQ;SignalRX_rec = func_KSE(R,RN,K,Mode_Map4,Mode_Type4);end%KSENerr = Nerr + sum(SignalRX_rec(:,1)~=SignalTx);Num = Num + 1;endBers(j) = Nerr/Num/Ntant/2;
end
A01-100三、测试结果
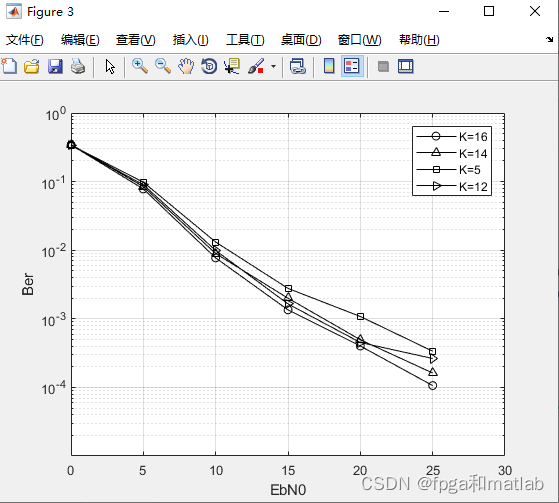
a01-100
这篇关于MIMO系统中基于K-Best的球形译码算法的matlab仿真的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






