（二）Tiki-taka算法（TTA）求解无人机三维路径规划研究（MATLAB）

本文主要是介绍（二）Tiki-taka算法（TTA）求解无人机三维路径规划研究（MATLAB），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、无人机模型简介：

单个无人机三维路径规划问题及其建模_IT猿手的博客-CSDN博客

参考文献：

[1]胡观凯,钟建华,李永正,黎万洪.基于IPSO-GA算法的无人机三维路径规划[J].现代电子技术,2023,46(07):115-120

二、Tiki-taka算法（TTA）简介

极致攻守算法（Tiki-Taka Algorithm，TTA）由Mohd Fadzil Faisae Ab. Rashid于2020年提出，该算法受tiki-taka 足球风格的短传、球员定位和保持控球的特点所启发。其旨在控制控球权并利用其战术优势击败对手，TTA算法新颖高效。单目标应用：Tiki-taka算法（TTA）求解太阳能光伏模型MATLAB_IT猿手的博客-CSDN博客

参考文献：

[1]Ab. Rashid, M.F.F. (2021), "Tiki-taka algorithm: a novel metaheuristic inspired by football playing style", Engineering Computations, Vol. 38 No. 1, pp. 313-343. Tiki-taka algorithm: a novel metaheuristic inspired by football playing style | Emerald Insight

[2]Zamli, Kamal Z , Kader, et al. Selective chaotic maps Tiki-Taka algorithm for the S-box generation and optimization.

三、TTA求解无人机路径规划

（1）部分代码

close all
clear  
clc
addpath('./Algorithm/')%添加算法路径
warning off;
%% 三维路径规划模型定义
global startPos goalPos N
N=2;%待优化点的个数(可以修改)
startPos = [10, 10, 80]; %起点(可以修改)
goalPos = [80, 90, 150]; %终点(可以修改)
SearchAgents_no=30; % 种群大小(可以修改)
Function_name='F2'; %F1:随机产生地图 F2：导入固定地图
Max_iteration=50; %最大迭代次数(可以修改)
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[Best_score,Best_pos,curve]=TTA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);%算法优化求解
AlgorithmName='TTA';%算法名字
figure
semilogy(curve,'Color','g','linewidth',3)
xlabel('迭代次数');
ylabel('飞行路径长度');
legend(AlgorithmName)
display(['算法得到的最优适应度: ', num2str(Best_score)]); 
Position=[Best_pos(1:dim/3); Best_pos(1+dim/3:2*(dim/3)); Best_pos(1+(2*dim/3):end)]'; %优化点的XYZ坐标（每一行是一个点）
plotFigure(Best_pos,AlgorithmName)%画最优路径

（2）部分结果

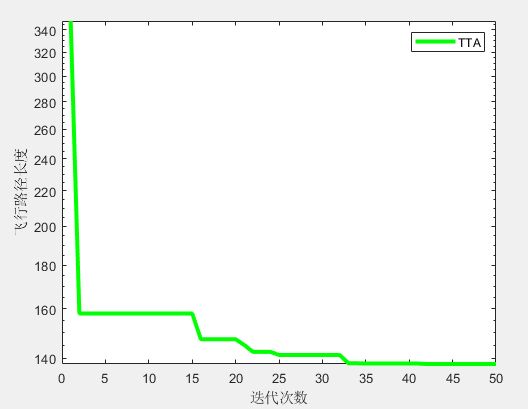
无人机飞行路径坐标：

   1.0000000e+01   1.0000000e+01   8.0000000e+011.0069761e+01   1.1125126e+01   8.0947246e+011.0158293e+01   1.2169888e+01   8.1882689e+011.0265680e+01   1.3137305e+01   8.2806728e+011.0392006e+01   1.4030396e+01   8.3719762e+011.0537355e+01   1.4852178e+01   8.4622189e+011.0701812e+01   1.5605672e+01   8.5514408e+011.0885461e+01   1.6293895e+01   8.6396818e+011.1088385e+01   1.6919866e+01   8.7269818e+011.1310670e+01   1.7486605e+01   8.8133807e+011.1552399e+01   1.7997129e+01   8.8989182e+011.1813656e+01   1.8454458e+01   8.9836344e+011.2094525e+01   1.8861610e+01   9.0675690e+011.2395092e+01   1.9221604e+01   9.1507620e+011.2715439e+01   1.9537458e+01   9.2332531e+011.3055651e+01   1.9812192e+01   9.3150824e+011.3415813e+01   2.0048823e+01   9.3962896e+011.3796008e+01   2.0250372e+01   9.4769146e+011.4196320e+01   2.0419855e+01   9.5569974e+011.4616835e+01   2.0560293e+01   9.6365777e+011.5057635e+01   2.0674704e+01   9.7156955e+011.5518805e+01   2.0766106e+01   9.7943906e+011.6000429e+01   2.0837518e+01   9.8727029e+011.6502592e+01   2.0891959e+01   9.9506723e+011.7025377e+01   2.0932448e+01   1.0028339e+021.7568869e+01   2.0962003e+01   1.0105742e+021.8133152e+01   2.0983643e+01   1.0182922e+021.8718309e+01   2.1000387e+01   1.0259918e+021.9324426e+01   2.1015253e+01   1.0336771e+021.9951587e+01   2.1031261e+01   1.0413520e+022.0599875e+01   2.1051428e+01   1.0490206e+022.1269375e+01   2.1078774e+01   1.0566867e+022.1960170e+01   2.1116317e+01   1.0643544e+022.2672346e+01   2.1167077e+01   1.0720278e+022.3405986e+01   2.1234070e+01   1.0797107e+022.4161174e+01   2.1320318e+01   1.0874071e+022.4937994e+01   2.1428837e+01   1.0951211e+022.5736532e+01   2.1562647e+01   1.1028566e+022.6556870e+01   2.1724767e+01   1.1106176e+022.7399094e+01   2.1918215e+01   1.1184082e+022.8263286e+01   2.2146009e+01   1.1262322e+022.9149532e+01   2.2411170e+01   1.1340938e+023.0057916e+01   2.2716714e+01   1.1419967e+023.0988521e+01   2.3065662e+01   1.1499452e+023.1941432e+01   2.3461032e+01   1.1579431e+023.2916733e+01   2.3905842e+01   1.1659944e+023.3914508e+01   2.4403111e+01   1.1741031e+023.4934842e+01   2.4955857e+01   1.1822733e+023.5977818e+01   2.5567101e+01   1.1905088e+023.7043521e+01   2.6239860e+01   1.1988137e+023.8132035e+01   2.6977152e+01   1.2071920e+023.9243444e+01   2.7781998e+01   1.2156476e+024.0377832e+01   2.8657415e+01   1.2241846e+024.1535284e+01   2.9606421e+01   1.2328069e+024.2715883e+01   3.0632037e+01   1.2415185e+024.3919714e+01   3.1737280e+01   1.2503234e+024.5146860e+01   3.2925169e+01   1.2592256e+024.6397407e+01   3.4198724e+01   1.2682291e+024.7671438e+01   3.5560962e+01   1.2773379e+024.8969037e+01   3.7014902e+01   1.2865559e+025.0290289e+01   3.8563563e+01   1.2958872e+025.1635278e+01   4.0209964e+01   1.3053356e+025.3004087e+01   4.1957123e+01   1.3149053e+025.4396802e+01   4.3808060e+01   1.3246002e+025.5813505e+01   4.5765792e+01   1.3344243e+025.7254282e+01   4.7833339e+01   1.3443816e+025.8719217e+01   5.0013719e+01   1.3544760e+026.0208393e+01   5.2309952e+01   1.3647116e+026.1721896e+01   5.4725054e+01   1.3750924e+026.3259808e+01   5.7262047e+01   1.3856222e+026.4822214e+01   5.9923947e+01   1.3963052e+026.6409199e+01   6.2713774e+01   1.4071453e+026.8020847e+01   6.5634547e+01   1.4181464e+026.9657241e+01   6.8689283e+01   1.4293127e+027.1318466e+01   7.1881003e+01   1.4406480e+027.3004606e+01   7.5212724e+01   1.4521563e+027.4715745e+01   7.8687466e+01   1.4638417e+027.6451968e+01   8.2308247e+01   1.4757081e+027.8213358e+01   8.6078085e+01   1.4877596e+028.0000000e+01   9.0000000e+01   1.5000000e+02