最优路径森林OPF

最优路径森林 OPF 算法将训练集转换成一个完全图，完全图中的每个节点都是调练集中的一个样本，图中的弧用节点间距离来表示，根据完全图来生成最优路径森林，森林中每棵树上的所有节点都属于同一个类别。在进行分类时，计算待分类样本到哪棵树的距离最近，则其类别就和这棵树的根节点的类别相同。

 OPF 分类器不依赖于任何参数，训练阶段不需要进行参数优化，因此其调练速度和分类速度都非常快。与其他分类算法相比，OPF 算法的分类精度和 SVM 相近而优于其他方法训练、分类速度比 SVM 更快，也不需要对类别的形状做任何假设，能处理多类及有一定程度类别重叠的问题。

OPF算法原理

分类器训练阶段

图（a）（b）中显示了5个训练集样本，其中圆形代表1类，六边形代表2类。

首先构建训练集样本的完全图，计算每两个节点之间的距离（可用欧式距离等衡量）

对此完全图计算最小生成树，在最小生成树中找到连接两个不同类别的节点的弧（图（b）中未显示，实际上就是画了圈的两个节点之间），对应的两个节点作为最优路径森林中的树的根节点。由于连接不同类别节点的弧可能有多个，所以同一类别的树的根节点也可能不止一个

节点上中的代表该节点的代价，代表该节点的标签。

初始时根节点的代价为0，非节点的代价设为无穷大。

更新非根节点的代价。的值即为最优路径上的前驱节点的代价与节点和之间距离的最大值。观察图（b）的右边，可以看到圆圈圈住的根节点的代价为0，与其相邻的节点代价为他们之间的距离0.2，不直接相邻的节点代价为它的前驱节点的代价0.2以及它同前驱节点之间的距离0.1之间的最大值0.2

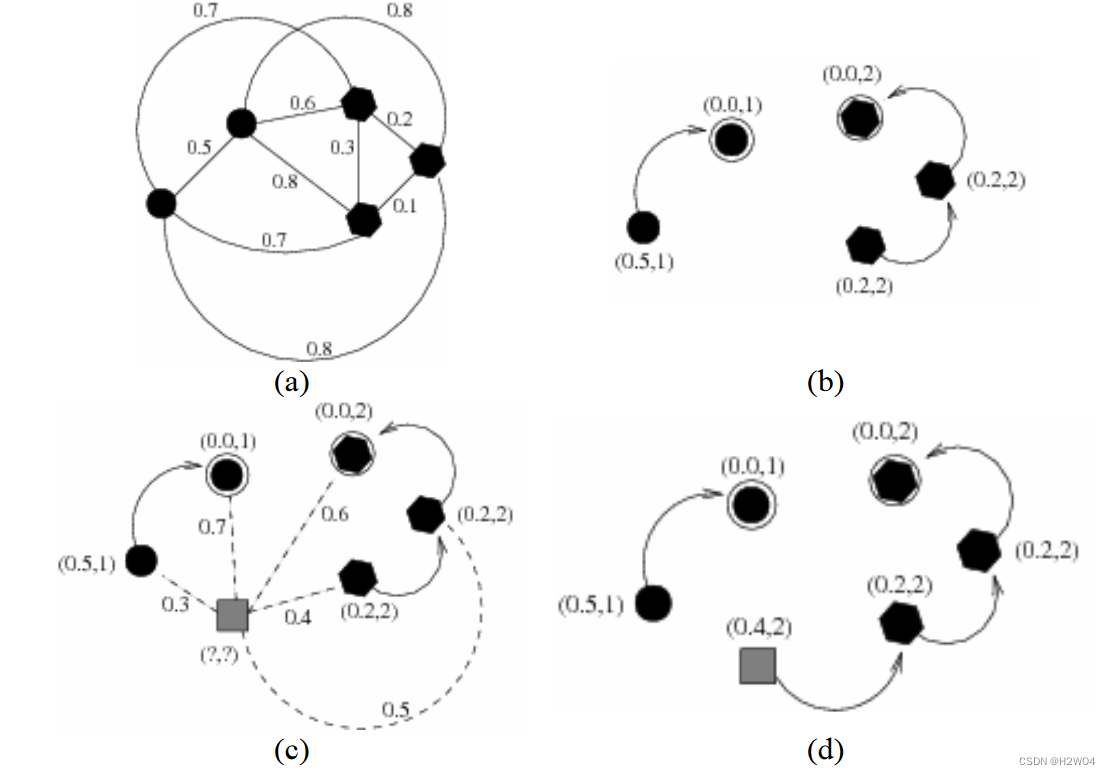
分类阶段

观察图（c）（d）

对于标签未知的灰方块样本，计算它到每个节点的距离。选取离它最近的根节点的标签作为它的标签，在图中与六边形的距离0.6小于与圆形的距离0.7，故将它分到2类，即使在整张图中离它最近的节点属于1类。代价更新规则同上。

相关的Python包-opfython

GitHub链接：https://github.com/gugarosa/opfython

介绍文档：https://opfython.readthedocs.io/

可直接使用pip安装

pip install opfython

以下是一个使用示例，选用了fashion-MNIST数据集

import torchvision
import torchvision.transforms as transforms # 数据处理模块
import opfython.math.general as g
import opfython.stream.splitter as s
from opfython.models import SupervisedOPF
minst=torchvision.datasets.FashionMNIST(root=r"D:\Code Storage\Pyworking\深度学习",download=False # true则要下载，false则代表文件地址下已经有数据，无需下载,train=True,transform=transforms.ToTensor())
x=minst.data.view(-1,28*28)
y=minst.targets
x_n=x[:5000].numpy()
y_n=y[:5000].numpy()# Splitting data into training and testing sets
X_train, X_test, Y_train, Y_test = s.split(x_n, y_n, percentage=0.5, random_state=1)# Creates a SupervisedOPF instance
opf = SupervisedOPF(distance="log_squared_euclidean", pre_computed_distance=None)# Fits training data into the classifier
opf.fit(X_train, Y_train)# Predicts new data
preds = opf.predict(X_test)# Calculating accuracy
acc = g.opf_accuracy(Y_test, preds)print(f"Accuracy: {acc}")

选取了5000条数据进行实验，其中2500条用于训练，2500条用于验证，运行大约需要40s，准确率为87%

参考文献

[1]沈龙凤, 宋万干, 葛方振, 李想, 杨忆, 刘怀愚, 高向军和洪留荣. 《最优路径森林分类算法综述》. 计算机应用研究 35, 期 1 (2018年): 7-12+23.

[2]Land Use Classification Using Optimum-Path Forest