【力扣周赛】第 369 场周赛（⭐记忆化搜索 树形DP）

本文主要是介绍【力扣周赛】第 369 场周赛（⭐记忆化搜索 树形DP），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

竞赛链接

https://leetcode.cn/contest/weekly-contest-369/

Q1：2917. 找出数组中的 K-or 值

https://leetcode.cn/problems/find-the-k-or-of-an-array/description/

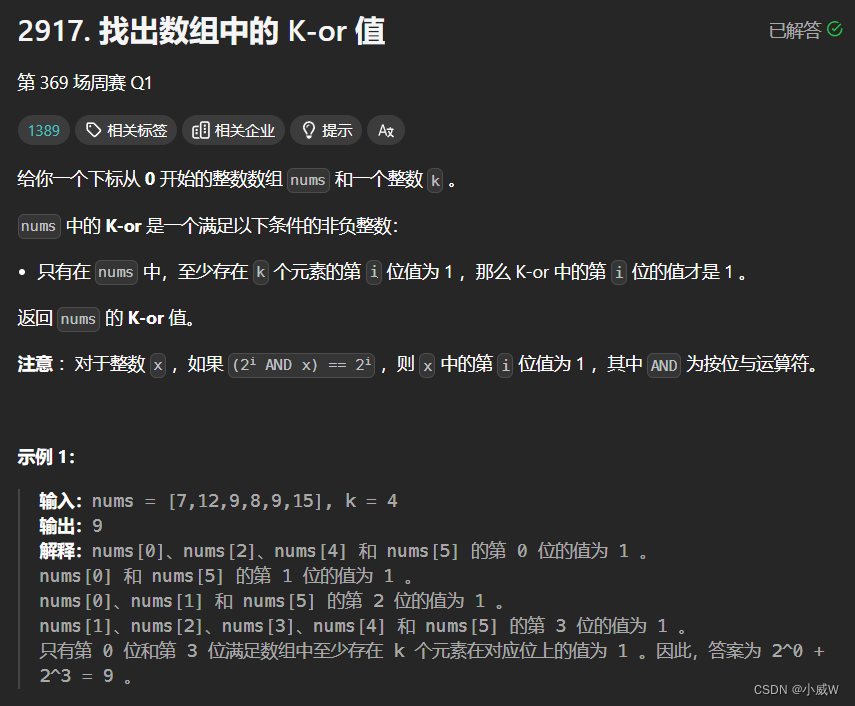
提示：
1 <= nums.length <= 50
0 <= nums[i] < 2^31
1 <= k <= nums.length

竞赛时代码——按题意模拟

class Solution {public int findKOr(int[] nums, int k) {int ans = 0;for (int i = 0; i < 31; ++i) {int c = 0;for (int x: nums) {if ((x >> i & 1) == 1) c++;}if (c >= k) ans |= 1 << i;}return ans;}
}

Q2：2918. 数组的最小相等和

https://leetcode.cn/problems/minimum-equal-sum-of-two-arrays-after-replacing-zeros/description/

提示：
1 <= nums1.length, nums2.length <= 10^5
0 <= nums1[i], nums2[i] <= 10^6

竞赛时代码——分类讨论

class Solution {public long minSum(int[] nums1, int[] nums2) {long s1 = 0, s2 = 0;int cnt1 = 0, cnt2 = 0;for (int x: nums1) {s1 += x;if (x == 0) cnt1++;}for (int x: nums2) {s2 += x;if (x == 0) cnt2++;}if (s1 < s2 + cnt2 && cnt1 == 0) return -1;if (s1 + cnt1 > s2 && cnt2 == 0) return -1;return Math.max(s1 + cnt1, s2 + cnt2);}
}

Q3：2919. 使数组变美的最小增量运算数⭐⭐⭐

https://leetcode.cn/problems/minimum-increment-operations-to-make-array-beautiful/description/

提示：
3 <= n == nums.length <= 10^5
0 <= nums[i] <= 10^9
0 <= k <= 10^9

竞赛时代码——动态规划

写的有点丑陋，但好歹是过了。

class Solution {public long minIncrementOperations(int[] nums, int k) {int n = nums.length;long[][] dp = new long[n + 1][2];       // dp[i][j]表示到第i个位置，选或不选且满足条件时的最小增量for (int i = 0; i <= n; ++i) Arrays.fill(dp[i], Long.MAX_VALUE);dp[0][0] = 0;dp[1][1] = Math.max(0, k - nums[0]);for (int i = 1; i <= n; ++i) {long x = nums[i - 1];if (i - 1 >= 0) {       // 前一个dp[i][0] = Math.min(dp[i][0], dp[i - 1][1]);dp[i][1] = Math.min(dp[i][1], Math.min(dp[i - 1][0], dp[i - 1][1]) + Math.max(0, k - x));}if (i - 2 >= 0) {       // 前两个dp[i][0] = Math.min(dp[i][0], dp[i - 2][1]);if (i - 3 >= 0) dp[i][1] = Math.min(dp[i][1], Math.min(dp[i - 2][1], i - 3 == 0? 0: dp[i - 3][1]) + Math.max(0, k - x));else dp[i][1] = Math.min(dp[i][1], Math.min(dp[i - 2][1], dp[i - 2][0]) + Math.max(0, k - x));}}if (dp[n][0] > dp[n][1]) return dp[n][1];return dp[n][0];}
}

解法2——记忆化搜索 翻译成递推

https://leetcode.cn/problems/minimum-increment-operations-to-make-array-beautiful/solutions/2503157/qiao-miao-she-ji-zhuang-tai-xuan-huo-bu-8547u/

dfs(i,j)表示前0~i个数字，且后面有j个不到k的数字，此时的最小花费

class Solution {int n, k;int[] nums;long[][] memo;public long minIncrementOperations(int[] nums, int k) {n = nums.length;this.k = k;this.nums = nums;memo = new long[n][3];for (long[] m: memo) Arrays.fill(m, -1);return dfs(n - 1, 0);}// dfs(i,j)表示前0~i个数字，且后面有j个不到k的数字，此时的最小花费public long dfs(int i, int j) {if (i < 0) return 0;if (memo[i][j] != -1) return memo[i][j];long res = dfs(i - 1, 0) + Math.max(0, k - nums[i]);    // 增加当前位置if (j < 2) res = Math.min(res, dfs(i - 1, j + 1));      // j<2时，可以不增加当前位置return memo[i][j] = res;}
}

---

1：1翻译成递推

自己改成了下面这样子。

class Solution {public long minIncrementOperations(int[] nums, int k) {int n = nums.length;// dp[i][j]表示到下标i，前面有j个位置没有到k(包括当前位置)long[][] dp = new long[n + 1][3];for (int i = 0; i < n; ++i) {for (int j = 0; j < 3; ++j) {dp[i + 1][j] = dp[i][2] + Math.max(0, k - nums[i]);     // 不得不选if (j > 0) {dp[i + 1][j] = Math.min(dp[i + 1][j], dp[i][j - 1]);// 可以不选}}}return Arrays.stream(dp[n]).min().getAsLong();}
}

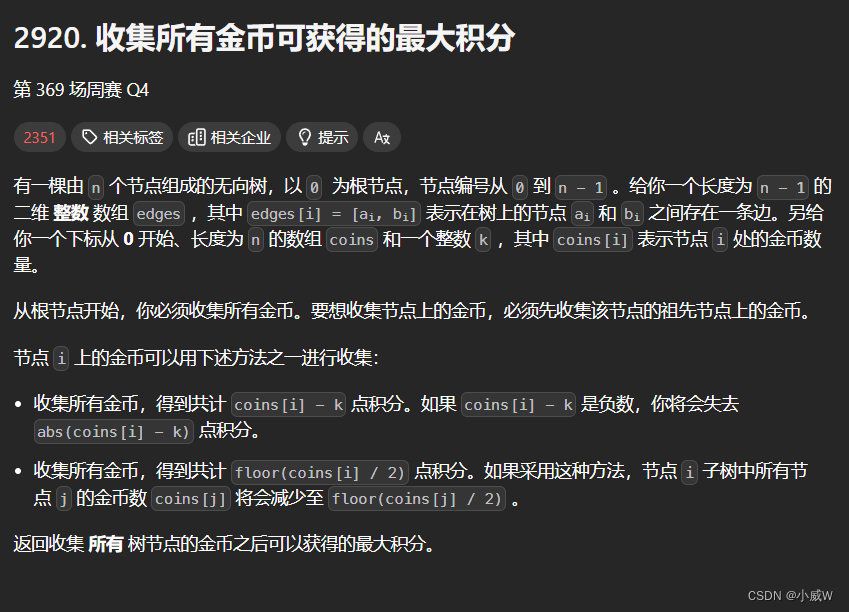
Q4：2920. 收集所有金币可获得的最大积分⭐⭐⭐⭐⭐🐂

https://leetcode.cn/problems/maximum-points-after-collecting-coins-from-all-nodes/description/

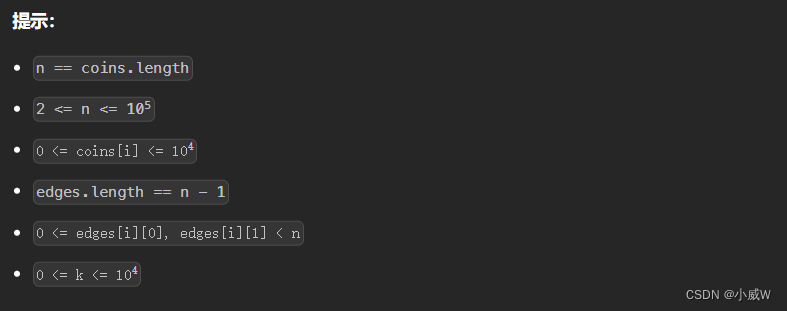
解法1——自顶向下（记忆化搜索）

https://leetcode.cn/problems/maximum-points-after-collecting-coins-from-all-nodes/solutions/2503152/shu-xing-dp-ji-yi-hua-sou-suo-by-endless-phzx/

class Solution {List<Integer>[] g;int[] coins;int k;int[][] memo;public int maximumPoints(int[][] edges, int[] coins, int k) {int n = edges.length + 1;this.coins = coins;this.k = k;g = new ArrayList[n];Arrays.setAll(g, e -> new ArrayList<>());for (int[] e: edges) {g[e[0]].add(e[1]);g[e[1]].add(e[0]);}memo = new int[n][14];      // 该题目数据下最多右移14次变成0for (int i = 0; i < n; ++i) {Arrays.fill(memo[i], -1);}return dfs(0, -1, 0);}public int dfs(int x, int fa, int d) {if (memo[x][d] != -1) return memo[x][d];int res1 = (coins[x] >> d) - k;int res2 = coins[x] >> (d + 1);for (int y: g[x]) {if (y == fa) continue;res1 += dfs(y, x, d);if (d < 13) {res2 += dfs(y, x, d + 1);}}return memo[x][d] = Math.max(res1, res2);}
}

解法2——自底向上

自底向上每个节点都只会枚举一遍，不需要 记忆数组了。

class Solution {List<Integer>[] g;int[] coins;int k;public int maximumPoints(int[][] edges, int[] coins, int k) {int n = edges.length + 1;this.coins = coins;this.k = k;g = new ArrayList[n];Arrays.setAll(g, e -> new ArrayList<>());for (int[] e: edges) {g[e[0]].add(e[1]);g[e[1]].add(e[0]);}return dfs(0, -1)[0];}public int[] dfs(int x, int fa) {int[] res1 = new int[14], res2 = new int[14];// 先得到各个子节点的结果for (int y: g[x]) {if (y != fa) {int[] r = dfs(y, x);for (int j = 0; j < 14; ++j) {res1[j] += r[j];if (j < 13) res2[j] += r[j + 1];}}}// 再逐个处理for (int j = 0; j < 14; ++j) {res1[j] = Math.max(res1[j] + (coins[x] >> j) - k, res2[j] + (coins[x] >> (j + 1)));}return res1;}
}

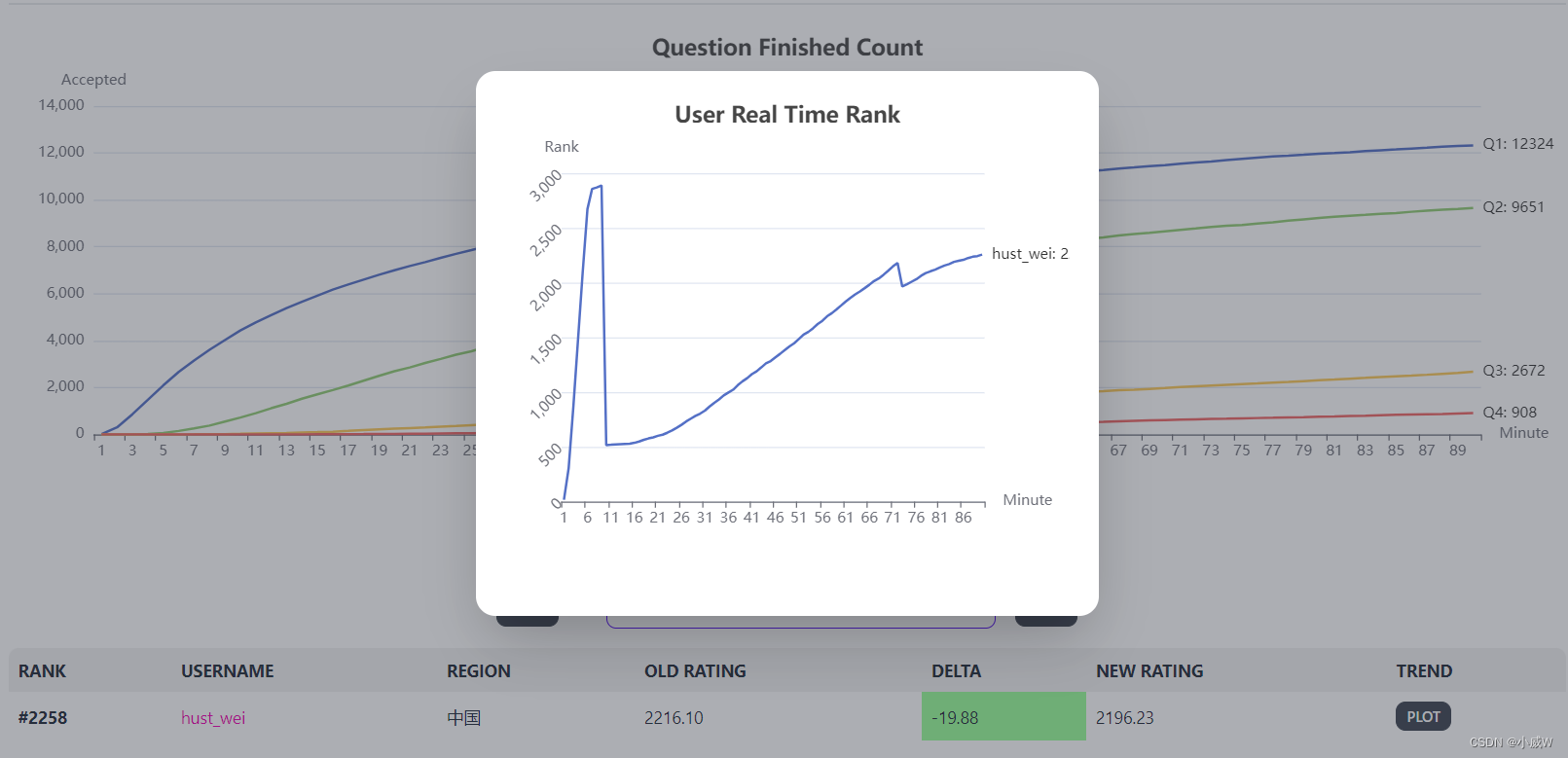
成绩记录

多的不说，排名挺吉利的。。
无奈遗憾掉分。

这篇关于【力扣周赛】第 369 场周赛（⭐记忆化搜索 树形DP）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---