本文主要是介绍Peter算法小课堂—差分与前缀和,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
差分
Codeforces802 D2C C++代码详解 差分_哔哩哔哩_bilibili
一维差分
差分与前缀和可以说成减法和加法的关系、除法和乘法的关系、积分和微分的关系(听不懂吧)
给定数组A,S为A的前缀和数组,则A为S的差分数组

差分数组构造
现在有了前缀和数组,就要推导差分数组,数学上有个递推公式:An=Sn-S(n-1)。其中A为差分,S为前缀和。这个公式只需要记住差分数组是什么就行。
差分数组应用
差分有什么用呢?差分可以使一个数组S中一段区间每个元素加上常数C。比如说:有任意一个数组S,区间[l,r]内每一个元素均加上常数j。若用暴力,枚举[l,r]中每一个元素,加j,时间复杂度为O(n),显然有更快的算法。若用差分,假设S的差分数组为A,则在A中标记第l个加j,第r+1个减j,这时再把差分数组化成前缀和数组,即可得到目标数组,时间复杂度O(n)
话不多说,让我们写代码八
输入长度为n的整数序列
接下来输入m个操作,每个操作包含三个整数 l,r,c,表示将序列中 [ l, r ] 之间的每个数加上c。
输入格式
第一行包含两个整数n和m。
第二行包含n个这个数,表示整数序列。
接下来m行,每行包括三个整数 l,r,c,表示一个操作
#include <iostream>using namespace std;const int N = 1e6 + 10;int a[N];int b[N];void insert(int l, int r, int c)
{b[l] += c;b[r + 1] -= c;
}int main()
{int n, m;cin >> n >> m;for (int i = 1; i <= n; i++){cin >> a[i];}for (int i = 1; i <= n; i++){insert(i, i, a[i]);}while (m--){int l, r, c;cin >> l >> r >> c;insert(l, r, c);}for (int i = 1; i <= n; i++){b[i] += b[i - 1];cout << b[i] << ' ';}return 0;
}
太戈编程736题
题目描述
你是一只汪星人,地球毁灭后你回到了汪星,这里每天有n个小时,你需要为自己选择正好连续的m小时作为每天睡眠的时间。从凌晨开始,第i小时内的睡眠质量为xi,请问经过选择后,你的睡眠质量总和最大是多少?
法1

cin>>n>>m;
for(int i=1;i<=n;i++) cin>>x[i];
for(int i=n+1;i<=n*2;i++) x[i]=x[i-n];
s[0]=0;
for(int i=1;i<=n*2;i++) s[i]=s[i-1]+x[i];
int ans=s[m];
for(int i=m+1;i<=n*2;i++)ans=max(ans,s[i]-s[i-m]);
cout<<ans<<endl;法2

cin>>n>>m;
for(int i=1;i<=n;i++) cin>>x[i];
for(int i=1;i<=n;i++) s[i]=s[i-1]+x[i];
int ans=s[m];
for(int i=m+1;i<=;i++)ans=max(ans,s[i]-s[i-m]);
for(int i=1;i<=m-1;i++)ans=max(ans,s[i]+s[n]-s[n-m+i]);
cout<<ans<<endl; 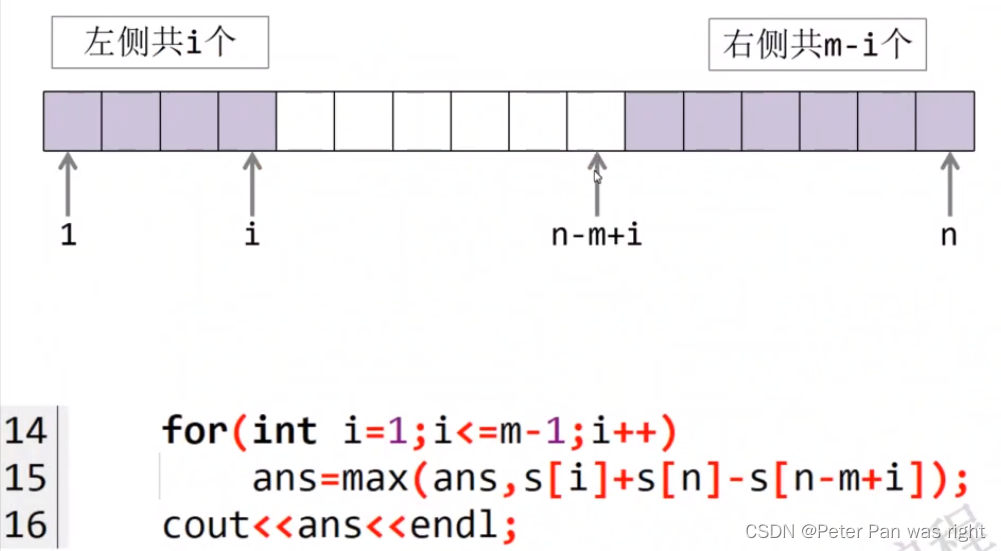
注意:数组下标要仔细分析
太戈编程第650题
思考五分钟……
cin>>n;
for(int i=1;i<=n;i++){cin>>a>>b>>x;d[a]+=x;d[b+5]-=x;
}
for(int i=1;i<R;i++)s[j]=s[i-1]+d[i];
cout<<*max_element(s+1,s+R)<<endl;希望这些对大家有用,三连必回
这篇关于Peter算法小课堂—差分与前缀和的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








