载波同步matlab,基于Matlab的载波同步建模与仿真（科斯塔斯环）——超全原理讲解，超全代码和图(这篇终于看懂了！)...

文章目录

1 设计原理

1.1 载波同步的原理

1.1.1 平方环载波同步法原理

1.1.2 科斯塔斯环载波同步法原理

1.2 二进制移相键控(2PSK)的原理

1.3 复信号

2 仿真实现

2.1 2PSK信号载波提取及解调仿真设计流程及原理

2.1.1 产生数字基带信号

2.1.2 产生载波信号

2.1.3 调制产生2PSK信号

2.1.4 锁相环参数清零及初始化

2.1.5 科斯塔斯环的正式处理过程

2.1.6 原始载波与提取载波

2.1.7 调制信号与解调信号

2.2 DSB信号载波提取及解调仿真设计流程及原理

2.2.1 产生正弦波模拟信号

2.2.2 产生载波信号

2.2.3 调制产生DSB信号

2.2.4 锁相环参数清零及初始化

2.2.5 科斯塔斯环的正式处理过程

2.2.6 原始载波与提取载波

2.2.7 调制信号与解调信号

2.3 2PSK信号载波同步及解调仿真结果

2.4 DSB信号载波同步及解调仿真结果

2.5 仿真结果分析

3 心得体会

4 参考文献

5 资源链接

1 设计原理

1.1 载波同步的原理

载波同步又称载波恢复( carrier restoration)，即在接收设备中产生一个和接收信号的载波同频同相的本地振荡( local oscillation)，供给解调器作相干解调用。当接收信号中包含离散的载频分量时，在接收端需要从信号中分离出信号载波作为本地相干载波；这样分离出的本地相干载波频率必然与接收信号载波频率相同，但为了使相位也相同，可能需要对分离出的载波相位作适当的调整。若接收信号中没有离散载波分量，例如在2PSK信号中(“1”和“0”以等 概率出现时)，则接收端需要用较复杂的方法从信号中提取载波。因此，在这些接收设备中需要有载波同步电路，以提供相干解调所需要的相干载波，相干载波必须与接收信号的载波严格地同频同相。

造成载波不同步的原因有:

·任何两个独立的振荡器都是不同步的;

·即便发射机和接收机使用的两个独立振荡器是同步的，电磁波在信道中的传播也会引起对接收机来说是未知的相位变化。比如电磁波的行程相位(一个波长的距离对应2π相移)，绕射、反射、散射引起的附加相移等，另外多普勒现象也会引起频率抖动。通常θ(t)\theta

(t)θ(t)相对于信息信号是缓慢变化的，因此经常写成 的形式。这里虽然 θ\thetaθ 不为0，但却是固定的，如果接收端已知其数值，则这两个载波在实质上是同步的。不过做相干解调时，需要对本地载波做相移以消除这个 θ\thetaθ 。

载波提取的目的：

要在接收端建立一个和发送信号完全一致(同频同相)的本地载波(称此为相干载波或同步载波)。

提取载波的方法：

一般分为两类：

一类是不专门发送导频，而在接收端直接从发送信号中提取载波，这类方法称为直接法，也称为自同步法；

另一类是在发送有用信号的同时，在适当的频率位置上，插入一个(或多个)称作导频的正弦波，接收端就利用导频提取出载波，这类方法称为插入导频法，也称为外同步法。

本篇报告主要介绍直接法提取载波中的平方环法和科斯塔斯环(Costas环)法提取相干载波的原理，并利用MATLAB程序仿真实现科斯塔斯环(Costas环)法分别对2PSK信号和DSB信号进行载波提取并解调出原始信号。

1.1.1 平方环载波同步法原理

设调制信号为m(t)m(t)m(t)，m(t)m(t)m(t)中无直流分量，则抑制载波的双边带信号为

s(t)=m(t)∗cos⁡ωct(1.1)\text{s}(t)=m(t)*\cos {{\omega }_{c}}t \tag {1.1}s(t)=m(t)∗cosωc​t(1.1)

接收端将该信号进行平方变换，即经过一个平方律部件后就得到

e(t)=m2(t)∗cos⁡2ωct=12m2(t)+12m2(t)cos⁡2ωct(1.2)e(t)={{m}^{2}}(t)*{{\cos }^{2}}{{\omega }_{c}}t=\frac{1}{2}{{m}^{2}}(t)+\frac{1}{2}{{m}^{2}}(t)\cos 2{{\omega }_{c}}t \tag {1.2}e(t)=m2(t)∗cos2ωc​t=21​m2(t)+21​m2(t)cos2ωc​t(1.2)

由上式可以看出，虽然前面假设m(t)m(t)m(t)中无直流分量，但 却一定有直流分量，这是因为m2(t){{m}^{2}}(t)m2(t)必为大于等于0的数，因此，m2(t){{m}^{2}}(t)m2(t)的均值必大于0，而这个均值就是直流分量，这样e(t)e(t)e(t)的第二项中就包含2fc2{{f}_{c}}2fc​频率的分量。例如，对于2PSK信号，为双极性矩形脉冲序列，设 =±1，那么m2(t){{m}^{2}}(t)m2(t)=1，这样经过平方率部件后可以得到

e(t)=m2(t)∗cos⁡2ωct=12+12cos⁡2ωct(1.3)e(t)={{m}^{2}}(t)*{{\cos }^{2}}{{\omega }_{c}}t=\frac{1}{2}+\frac{1}{2}\cos 2{{\omega }_{c}}t\tag {1.3}e(t)=m2(t)∗cos2ωc​t=21​+21​cos2ωc​t(1.3)

由上式可知，通过2fc2{{f}_{c}}2fc​窄带滤波器从中很容易取出2fc2{{f}_{c}}2fc​频率分量。经过一个二分频器就可以得到2fc2{{f}_{c}}2fc​的频率成分，这就是所需要的同步载波。因而，利用图1-1所示的方框图就可以提取出载波。

图1-1 平方变换法提取载波原理框图

为了改善平方变换的性能，可以在平方变换法的基础上，把窄带滤波器用锁相环替代，构成如图1-2所示框图，这样就实现了平方环法提取载波。由于锁相环具有良好的跟踪、窄带滤波和记忆性能，因此平方环法比一般的平方变换法具有更好的性能，因而得到广泛的应用。

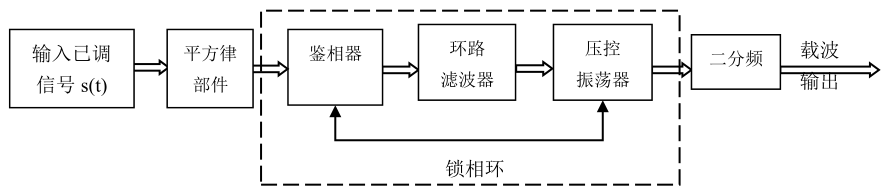
图1-2 平方环法提取载波原理框图

1.1.2 科斯塔斯环载波同步法原理

科斯塔斯(Costas)环法又称同相正交环法或边环法。相比于平方环法，它仍然利用锁相环提取载频，但是不需要对接收信号作平方运算就能得到载频输出。在载波频率上进行平方运算后，由于频率倍增,使后面的锁相环工作频率加倍，实现的难度增大。科斯塔斯环则用相乘器和较简单的低通滤波器取代平方器;这是它的主要优点。它和平方环法的性能在理论上是一样的。

图1-2中示出了其原理方框图。图中，接收信号s(t)s(t)s(t)被送入二路相乘器，两相乘器输入的a点和b点的压控振荡电压分别为

va=cos⁡(ωct+φ)(1.4){{v}_{a}}=\cos ({{\omega }_{c}}t+\varphi )\tag {1.4}va​=cos(ωc​t+φ)(1.4)va=sin⁡(ωct+φ)(1.5){{v}_{a}}=\sin ({{\omega }_{c}}t+\varphi )\tag {1.5}va​=sin(ωc​t+φ)(1.5)

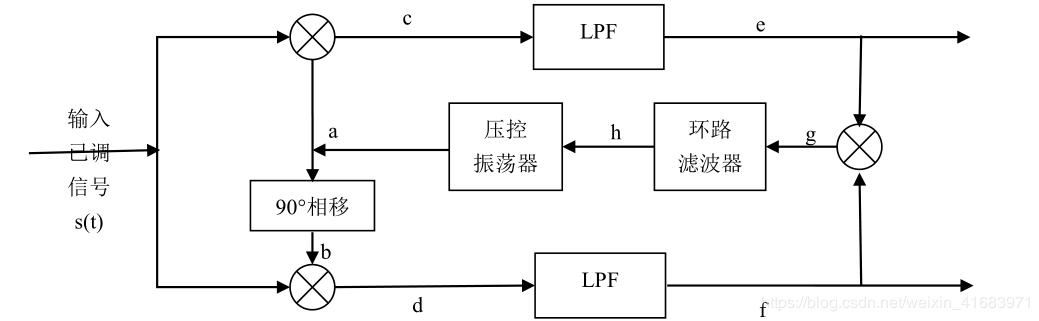
图1-3 科斯塔斯环法提取载波原理框图

它们和接收信号电压相乘后，得到c点和d点的电压为

vc=m(t)cos⁡(ωct+θ)cos⁡(ωct+φ)=1