【RT-DETR改进】SIoU、GIoU、CIoU、DIoU、AlphaIoU等二十余种损失函数

2023-11-29 22:04
文章标签 函数 改进 损失 rt siou alphaiou detr giou diou ciou 二十余种

本文主要是介绍【RT-DETR改进】SIoU、GIoU、CIoU、DIoU、AlphaIoU等二十余种损失函数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1c968e8b8bfa44a59ed2174cec6cc5a8.gif

一、本文介绍

这篇文章介绍了RT-DETR的重大改进，特别是在损失函数方面的创新。它不仅包括了多种IoU损失函数的改进和变体，如SIoU、WIoU、GIoU、DIoU、EIOU、CIoU，还融合了“Alpha”思想，创造了一系列新的损失函数。这些组合形式的损失函数超过了二十余种，每种都针对特定的目标检测挑战进行优化。文章会详细探讨这些损失函数如何提高RT-DETR在各种检测任务中的性能，包括提升精度、加快收敛速度和增强模型对复杂场景的适应性。本文章主要是为了发最近新出的Inner思想改进的各种EIoU的文章服务，其中我经过实验在绝大多数下的效果都要比本文中提到的各种损失效果要好。 

  RT-DETR改进专栏：RT-DETR专栏——持续复现各种顶会内容——论文收割机

InnerIoU： RT-DETR改进 | 2023小目标改进 | InnerEIoU、InnerSIoU、InnerWIoU、InnerDIoU等二十余种损失函数

目录

一、本文介绍

二、各种损失函数的基本原理 

2.1 交集面积和并集面积

2.2 IoU

2.3 SIoU

2.4 WioU

2.5 GIoU

2.6 DIoU

2.7 EIoU

2.8 CIoU

三、EIoU、SIoU、EIoU、WIoU等损失函数代码块

四、添加EIoU、SIoU、EIoU、AlphaIoU等损失函数到模型中

7.1 修改一

7.2 修改二

五、总结

二、各种损失函数的基本原理 

2.1 交集面积和并集面积

在理解各种损失函数之前我们需要先来理解一下交集面积和并集面积，在数学中我们都学习过集合的概念，这里的交集和并集的概念和数学集合中的含义是一样的。

2d28de8702034e14955f6834c19c3edb.png

​

2.2 IoU

论文地址：IoU Loss for 2D/3D Object Detectio

适用场景：普通的IoU并没有特定的适用场景

概念: 测量预测边界框和真实边界框之间的重叠度(最基本的边界框损失函数，后面的都是居于其进行计算)。

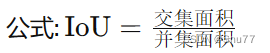
2fbd3fd1fc2f451bb237de0e36c4ba2e.png

​

2.3 SIoU

论文地址：SIoU: More Powerful Learning for Bounding Box Regression

适用场景：适用于需要高精度边界框对齐的场景，如精细的物体检测和小目标检测。

概念: SIoU损失通过融入角度考虑和规模敏感性，引入了一种更为复杂的边界框回归方法，解决了以往损失函数的局限性，SIoU损失函数包含四个组成部分：角度损失、距离损失、形状损失和第四个未指定的组成部分。通过整合这些方面，从而实现更好的训练速度和预测准确性。

9817889f4fe140b7a914acf93773d538.png

​

2.4 WioU

论文地址：WIoU: Bounding Box Regression Loss with Dynamic Focusing Mechanism

适用场景：适用于需要动态调整损失焦点的情况，如不均匀分布的目标或不同尺度的目标检测。

概念:引入动态聚焦机制的IoU变体，旨在改善边界框回归损失。

05b8bd2d7bcb4df7a0fa5c44c9201bf7.png

​

2.5 GIoU

论文地址：GIoU: A Metric and A Loss for Bounding Box Regression

适用场景：适合处理有重叠和非重叠区域的复杂场景，如拥挤场景的目标检测。

概念: 在IoU的基础上考虑非重叠区域，以更全面评估边界框

9ca4394b9cd74103b4100129a8eaf26c.png

​

2.6 DIoU

论文地址：DIoU: Faster and Better Learning for Bounding Box Regression

适用场景：适用于需要快速收敛和精确定位的任务，特别是在边界框定位精度至关重要的场景。

概念:结合边界框中心点之间的距离和重叠区域。

48175f62983a4d0aba517180582a7060.png

​

2.7 EIoU

论文地址：EIoU:Loss for Accurate Bounding Box Regression

适用场景：可用于需要进一步优化边界框对齐和形状相似性的高级场景。

概念:EIoU损失函数的核心思想在于提高边界框回归的准确性和效率。它通过以下几个方面来优化目标检测：

1. 增加中心点距离损失：通过最小化预测框和真实框中心点之间的距离，提高边界框的定位准确性。

2. 考虑尺寸差异：通过惩罚宽度和高度的差异，EIoU确保预测框在形状上更接近真实框。

3. 结合最小封闭框尺寸：将损失函数与包含预测框和真实框的最小封闭框的尺寸相结合，从而使得损失更加敏感于对象的尺寸和位置。

EIoU损失函数在传统IoU基础上增加了这些考量，以期在各种尺度上都能获得更精确的目标定位，尤其是在物体大小和形状变化较大的场景中。

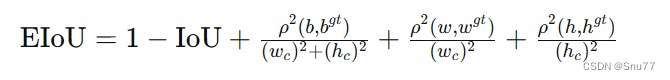
0e140b7de1094bab8fc00a6a63ab54f3.png

​

2.8 CIoU

论文地址：CIoU:Enhancing Geometric Factors in Model Learning

适用场景：适合需要综合考虑重叠区域、形状和中心点位置的场景，如复杂背景或多目标跟踪。

概念:综合考虑重叠区域、中心点距离和长宽比。

f08d2772845447058b1ede34d0042c38.png

三、EIoU、SIoU、EIoU、WIoU等损失函数代码块

import numpy as np
import torch, mathclass WIoU_Scale:''' monotonous: {None: origin v1True: monotonic FM v2False: non-monotonic FM v3}momentum: The momentum of running mean'''iou_mean = 1.monotonous = False_momentum = 1 - 0.5 ** (1 / 7000)_is_train = Truedef __init__(self, iou):self.iou = iouself._update(self)@classmethoddef _update(cls, self):if cls._is_train: cls.iou_mean = (1 - cls._momentum) * cls.iou_mean + \cls._momentum * self.iou.detach().mean().item()@classmethoddef _scaled_loss(cls, self, gamma=1.9, delta=3):if isinstance(self.monotonous, bool):if self.monotonous:return (self.iou.detach() / self.iou_mean).sqrt()else:beta = self.iou.detach() / self.iou_meanalpha = delta * torch.pow(gamma, beta - delta)return beta / alphareturn 1def bbox_iou(box1, box2, x1y1x2y2=True, GIoU=False, DIoU=False, CIoU=False, SIoU=False, EIoU=False, WIoU=False, alpha=1,gamma=0.5, scale=False, eps=1e-7):# Returns the IoU of box1 to box2. box1 is 4, box2 is nx4box2 = box2.T# Get the coordinates of bounding boxesif x1y1x2y2:  # x1, y1, x2, y2 = box1b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]else:  # transform from xywh to xyxyb1_x1, b1_x2 = box1[0] - box1[2] / 2, box1[0] + box1[2] / 2b1_y1, b1_y2 = box1[1] - box1[3] / 2, box1[1] + box1[3] / 2b2_x1, b2_x2 = box2[0] - box2[2] / 2, box2[0] + box2[2] / 2b2_y1, b2_y2 = box2[1] - box2[3] / 2, box2[1] + box2[3] / 2# Intersection areainter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * \(torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)).clamp(0)# Union Areaw1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + epsw2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + epsunion = w1 * h1 + w2 * h2 - inter + epsif scale:self = WIoU_Scale(1 - (inter / union))# IoU# iou = inter / union # ori iouiou = torch.pow(inter / (union + eps), alpha)  # alpha iouif CIoU or DIoU or GIoU or EIoU or SIoU or WIoU:cw = b1_x2.maximum(b2_x2) - b1_x1.minimum(b2_x1)  # convex (smallest enclosing box) widthch = b1_y2.maximum(b2_y2) - b1_y1.minimum(b2_y1)  # convex heightif CIoU or DIoU or EIoU or SIoU or WIoU:  # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1c2 = (cw ** 2 + ch ** 2) ** alpha + eps  # convex diagonal squaredrho2 = (((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2 + (b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4) ** alpha  # center dist ** 2if CIoU:  # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47v = (4 / math.pi ** 2) * (torch.atan(w2 / h2) - torch.atan(w1 / h1)).pow(2)with torch.no_grad():alpha_ciou = v / (v - iou + (1 + eps))return iou - (rho2 / c2 + torch.pow(v * alpha_ciou + eps, alpha))  # CIoUelif EIoU:rho_w2 = ((b2_x2 - b2_x1) - (b1_x2 - b1_x1)) ** 2rho_h2 = ((b2_y2 - b2_y1) - (b1_y2 - b1_y1)) ** 2cw2 = torch.pow(cw ** 2 + eps, alpha)ch2 = torch.pow(ch ** 2 + eps, alpha)return iou - (rho2 / c2 + rho_w2 / cw2 + rho_h2 / ch2)  # EIouelif SIoU:# SIoU Loss https://arxiv.org/pdf/2205.12740.pdfs_cw = (b2_x1 + b2_x2 - b1_x1 - b1_x2) * 0.5 + epss_ch = (b2_y1 + b2_y2 - b1_y1 - b1_y2) * 0.5 + epssigma = torch.pow(s_cw ** 2 + s_ch ** 2, 0.5)sin_alpha_1 = torch.abs(s_cw) / sigmasin_alpha_2 = torch.abs(s_ch) / sigmathreshold = pow(2, 0.5) / 2sin_alpha = torch.where(sin_alpha_1 > threshold, sin_alpha_2, sin_alpha_1)angle_cost = torch.cos(torch.arcsin(sin_alpha) * 2 - math.pi / 2)rho_x = (s_cw / cw) ** 2rho_y = (s_ch / ch) ** 2gamma = angle_cost - 2distance_cost = 2 - torch.exp(gamma * rho_x) - torch.exp(gamma * rho_y)omiga_w = torch.abs(w1 - w2) / torch.max(w1, w2)omiga_h = torch.abs(h1 - h2) / torch.max(h1, h2)shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), 4) + torch.pow(1 - torch.exp(-1 * omiga_h), 4)return iou - torch.pow(0.5 * (distance_cost + shape_cost) + eps, alpha)  # SIouelif WIoU:if scale:return getattr(WIoU_Scale, '_scaled_loss')(self), (1 - iou) * torch.exp((rho2 / c2)), iou  # WIoU https://arxiv.org/abs/2301.10051else:return iou, torch.exp((rho2 / c2))  # WIoU v1return iou - rho2 / c2  # DIoUc_area = cw * ch + eps  # convex areareturn iou - torch.pow((c_area - union) / c_area + eps, alpha)  # GIoU https://arxiv.org/pdf/1902.09630.pdfreturn iou  # IoU

四、添加EIoU、SIoU、EIoU、AlphaIoU等损失函数到模型中

7.1 修改一

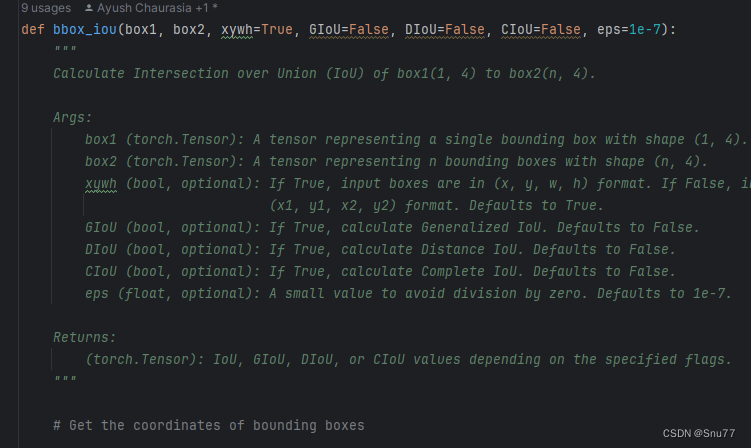
第一步我们需要找到如下的文件ultralytics/utils/metrics.py,找到如下的代码，下面的图片是原先的代码部分截图的正常样子，然后我们将上面的整个代码块将下面的整个方法(这里这是部分截图)内容全部替换

e7a59a4795ac45e29c2ee02d373394e9.png

7.2 修改二

第二步我们找到另一个文件如下->"ultralytics/models/utils/loss.py"，(注意这个文件和YOLOv8的修改内容不是一个！！！！)我们找到如下的代码块，我们就可以进行设置了，看到我这里以及将EIoU都设置成True了，并且引入了alpha的思想进行改进大家可以多进行尝试。

366e9c4d9220442baa0f634a58878d0c.png

(这里暂时还不能使用Focus的思想！！！)

五、总结

到此本文的正式分享内容就结束了，在这里给大家推荐我的RT-DETR改进有效涨点专栏，本专栏目前为新开的平均质量分98分，后期我会根据各种最新的前沿顶会进行论文复现，也会对一些老的改进机制进行补充，目前本专栏免费阅读(暂时，大家尽早关注不迷路~)，如果大家觉得本文帮助到你了，订阅本专栏，关注后续更多的更新~

本专栏其它内容(持续更新) 

 RT-DETR改进专栏：RT-DETR专栏——持续复现各种顶会内容——论文收割机

3d51a0611af1442f833362eaf18fbae2.gif

​​

这篇关于【RT-DETR改进】SIoU、GIoU、CIoU、DIoU、AlphaIoU等二十余种损失函数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/434481。

相关文章

Python的time模块一些常用功能(各种与时间相关的函数)

Python的time模块一些常用功能(各种与时间相关的函数)

《Python的time模块一些常用功能(各种与时间相关的函数)》Python的time模块提供了各种与时间相关的函数,包括获取当前时间、处理时间间隔、执行时间测量等,：本文主要介绍Python的... 目录1. 获取当前时间2. 时间格式化3. 延时执行4. 时间戳运算5. 计算代码执行时间6. 转换为指
阅读更多...
Python正则表达式语法及re模块中的常用函数详解

Python正则表达式语法及re模块中的常用函数详解

《Python正则表达式语法及re模块中的常用函数详解》这篇文章主要给大家介绍了关于Python正则表达式语法及re模块中常用函数的相关资料,正则表达式是一种强大的字符串处理工具,可以用于匹配、切分、... 目录概念、作用和步骤语法re模块中的常用函数总结 概念、作用和步骤概念： 本身也是一个字符串，其中
阅读更多...
shell编程之函数与数组的使用详解

shell编程之函数与数组的使用详解

《shell编程之函数与数组的使用详解》：本文主要介绍shell编程之函数与数组的使用,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录shell函数函数的用法俩个数求和系统资源监控并报警函数函数变量的作用范围函数的参数递归函数shell数组获取数组的长度读取某下的
阅读更多...
MySQL高级查询之JOIN、子查询、窗口函数实际案例

MySQL高级查询之JOIN、子查询、窗口函数实际案例

《MySQL高级查询之JOIN、子查询、窗口函数实际案例》：本文主要介绍MySQL高级查询之JOIN、子查询、窗口函数实际案例的相关资料,JOIN用于多表关联查询,子查询用于数据筛选和过滤,窗口函... 目录前言1. JOIN（连接查询）1.1 内连接（INNER JOIN）1.2 左连接（LEFT JOI
阅读更多...
MySQL中FIND_IN_SET函数与INSTR函数用法解析

MySQL中FIND_IN_SET函数与INSTR函数用法解析

《MySQL中FIND_IN_SET函数与INSTR函数用法解析》：本文主要介绍MySQL中FIND_IN_SET函数与INSTR函数用法解析,本文通过实例代码给大家介绍的非常详细,感兴趣的朋友一... 目录一、功能定义与语法1、FIND_IN_SET函数2、INSTR函数二、本质区别对比三、实际场景案例分
阅读更多...
C++ Sort函数使用场景分析

C++ Sort函数使用场景分析

《C++Sort函数使用场景分析》sort函数是algorithm库下的一个函数,sort函数是不稳定的,即大小相同的元素在排序后相对顺序可能发生改变,如果某些场景需要保持相同元素间的相对顺序,可使... 目录C++ Sort函数详解一、sort函数调用的两种方式二、sort函数使用场景三、sort函数排序
阅读更多...
C语言函数递归实际应用举例详解

C语言函数递归实际应用举例详解

《C语言函数递归实际应用举例详解》程序调用自身的编程技巧称为递归,递归做为一种算法在程序设计语言中广泛应用,：本文主要介绍C语言函数递归实际应用举例的相关资料,文中通过代码介绍的非常详细,需要的朋... 目录前言一、递归的概念与思想二、递归的限制条件 三、递归的实际应用举例（一）求 n 的阶乘（二）顺序打印
阅读更多...
C/C++错误信息处理的常见方法及函数

C/C++错误信息处理的常见方法及函数

《C/C++错误信息处理的常见方法及函数》C/C++是两种广泛使用的编程语言,特别是在系统编程、嵌入式开发以及高性能计算领域,：本文主要介绍C/C++错误信息处理的常见方法及函数,文中通过代码介绍... 目录前言1. errno 和 perror()示例：2. strerror()示例：3. perror(
阅读更多...
Kotlin 作用域函数apply、let、run、with、also使用指南

Kotlin 作用域函数apply、let、run、with、also使用指南

《Kotlin作用域函数apply、let、run、with、also使用指南》在Kotlin开发中,作用域函数（ScopeFunctions）是一组能让代码更简洁、更函数式的高阶函数,本文将... 目录一、引言：为什么需要作用域函数？二、作用域函China编程数详解1. apply：对象配置的 “流式构建器”最
阅读更多...
Android Kotlin 高阶函数详解及其在协程中的应用小结

Android Kotlin 高阶函数详解及其在协程中的应用小结

《AndroidKotlin高阶函数详解及其在协程中的应用小结》高阶函数是Kotlin中的一个重要特性,它能够将函数作为一等公民（First-ClassCitizen）,使得代码更加简洁、灵活和可... 目录1. 引言2. 什么是高阶函数？3. 高阶函数的基础用法3.1 传递函数作为参数3.2 Lambda
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2