本文主要是介绍U4_2:图论之MST/Prim/Kruskal,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 一、最小生成树-MST
- 生成MST策略
- 一些定义
- 思路
- 彩蛋
- 二、普里姆算法(Prim算法)
- 思路
- 算法流程
- 数据存储
- 分析
- 伪代码
- 时间复杂度分析
- 三、克鲁斯卡尔算法(Kruskal算法)
- 分析
- 算法流程
- 并查集-Find-set
- 伪代码
- 时间复杂度分析
一、最小生成树-MST
无向图,无环,所有点连通,边权重和最小
(没有权重标注就默认为1)
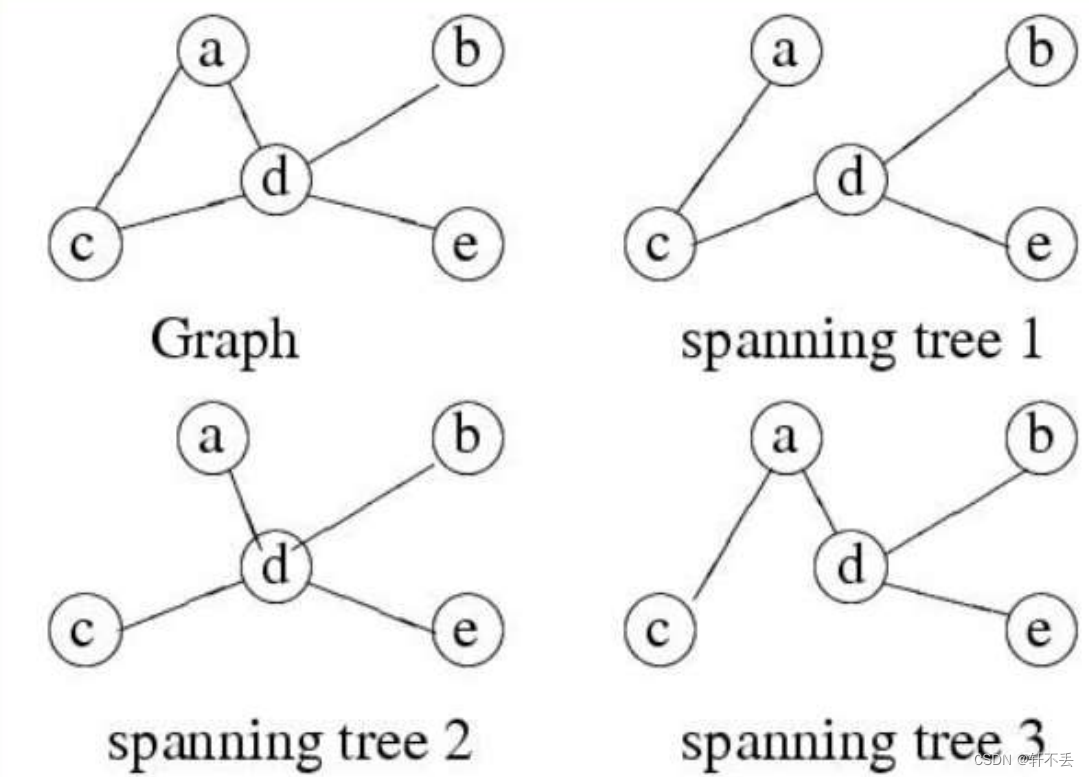
生成MST策略
- 从一个空图开始。
- 尝试一次添加一条边,始终确保所构建的保持无循环。
- 如果在添加了每条边之后,我们确定生成的图是某个最小生成树的子集,我们就完成了。
一些定义
集合 A A A是最小生成树 T T T的子集,当 A U ( u , v ) A\space U(u,v) A U(u,v)也是 M S T MST MST子集时, ( u , v ) (u,v) (u,v)是安全的。
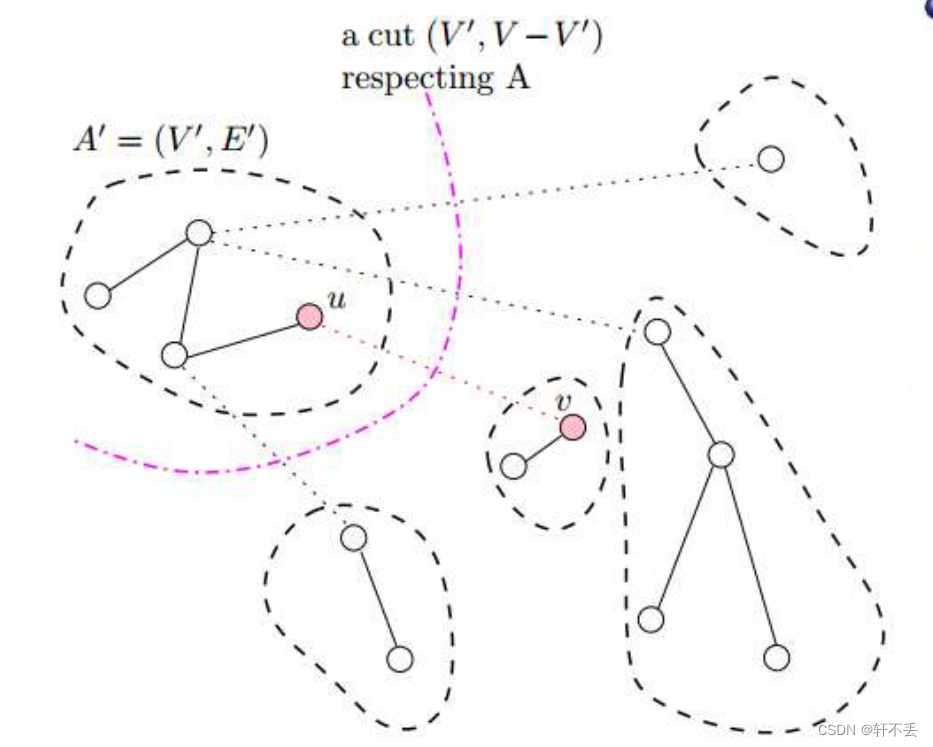
切割 c u t cut cut: ( S , V − S ) (S,V-S) (S,V−S)
a a a c u t cut cut r e s p e c t s respects respects a a a s e t set set A A A o f of of e d g e s edges edges i f if if n o no no e d g e s edges edges i n in in A A A c r o s s e s crosses crosses t h e the the c u t cut cut.
An edge is a light edge crossing a cut if its weight is the minimumof any edge crossing the cut
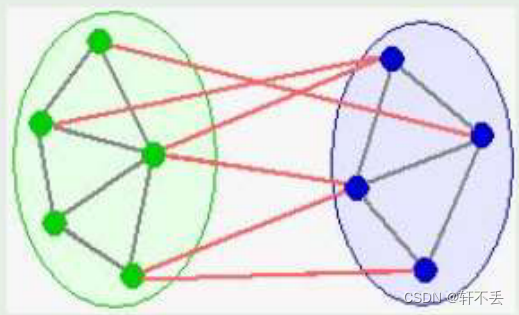
思路
(S, V - S) be any cut of G that respects A
(u, v) be a light edge crossing the cut (S, V - S)Then, edge (u, v) is safe for A.
则 lt means that we can find a safe edge by
- first finding a cut that respects A
- then finding the light edge crossingthat cut
That light edge is a safe edge
彩蛋
本质上下面所要讲的Prim算法和Kruskal算法都是依据这个总思路来的,先分隔cut,然后根据cut找light edge,最后不断生成MST
二、普里姆算法(Prim算法)
思路
- 首先选择任意顶点r作为树的根。
- 当树不包含图中的所有顶点时:找到离开树的最短边并将其添加到树中。
这个思路可以想到,每次的cut就是选入作为顶点的集合 S S S和未选入的顶点 G − S G-S G−S
算法流程
数据存储
区分cut:最初始是空集,所有顶点被标记为白色,选入的顶点标记为黑色
利用优先队列存储
利用优先队列(小顶堆)去寻找 t h e the the l i g h e s t lighest lighest e d g e edge edge(相应函数如下)
3. I n s e r t ( u , k e y ) Insert(u, key) Insert(u,key):用键值key在Q中插入u。
4. u = E x t r a c t − m i n ( ) u = Extract- min() u=Extract−min():提取键值最小的项。
5. D e c r e a s e − K e y ( u , n e w − k e y ) Decrease-Key(u, new-key) Decrease−Key(u,new−key):将u的键值减小为new-key
利用 p r e d [ A ] pred[A] pred[A]去存储每个顶点的存储顺序
分析
t h e the the l i g h e s t lighest lighest e d g e edge edge本质上是在黑白分界点的这些边中寻找,因此每次更新都需要维护这些点( k e y key key)。
初始的时候设为 i n i f i n i t y inifinity inifinity,每次加入新顶点时就找到它的所有边判断是否比现在的key是否更小了,如果更小了就可以更新并且换前驱
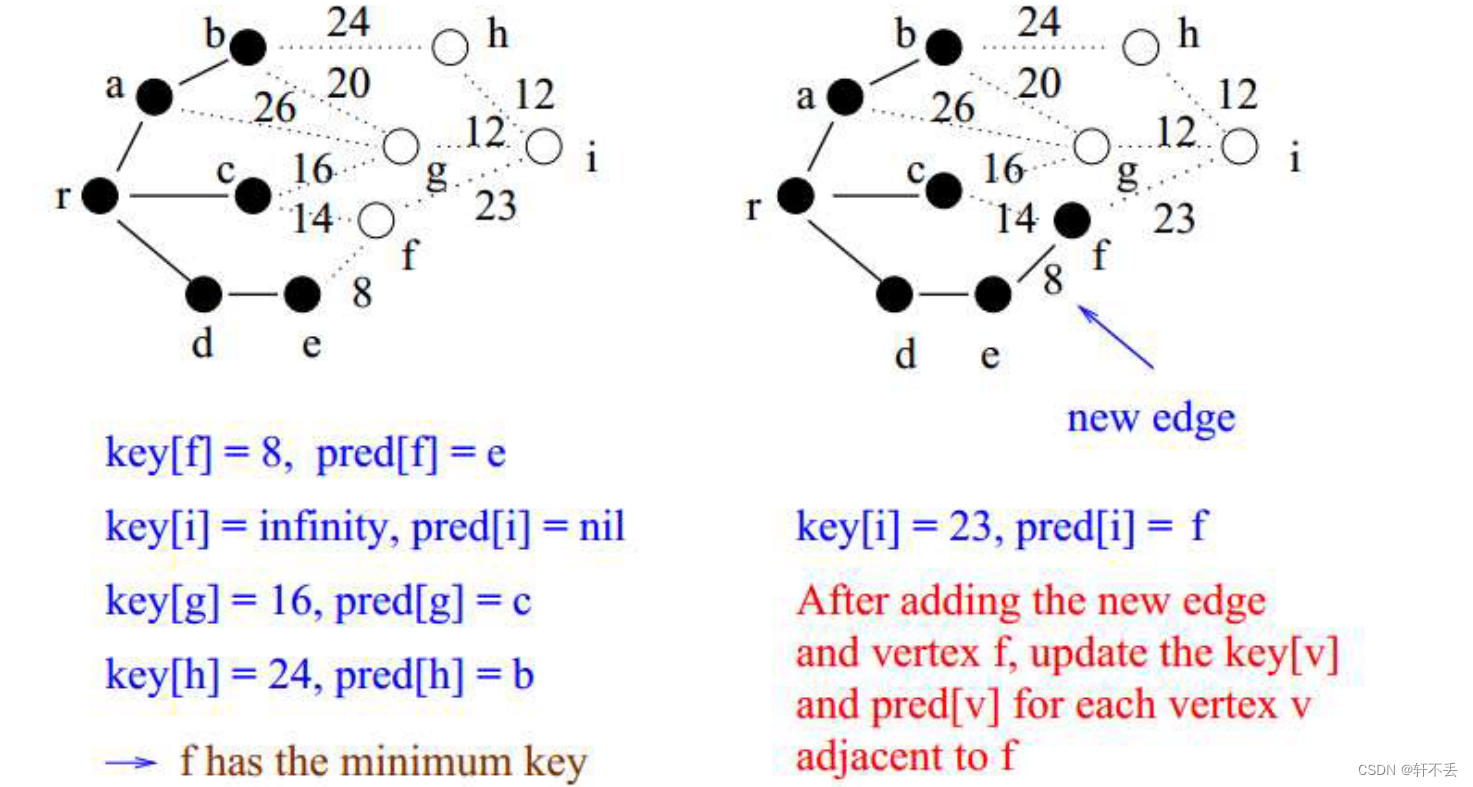
伪代码
for u ∈ V docolor[u] ← white,key[u] ← +∞
end
key[u] ← 0,pred[r] ← null; //最开始的顶点
Q ← new PriQueue(V)
while Q is noempty dou ← Q.Extract-Min(); //the lighest edge for v ∈ adj[u] doif(color[u] ← white && w[u,v] < key[u]) thenkey[u] ← w[u,v]Q.decrease-Key(v,key[u]) pred[v] ← uendendcolor[u] ← black
end
时间复杂度分析
创建优先队列 O ( V l o g V ) O(VlogV) O(VlogV),每次循环 E x t r a c t − M i n Extract-Min Extract−Min为 l o g ( V ) log(V) log(V),总共V个顶点,总时间复杂度为 O ( V l o g V ) O(VlogV) O(VlogV)。每次循环 D e c r e a s e − K e y Decrease-Key Decrease−Key为 O ( l o g V ) O(logV) O(logV),因为循环内每次更新都是针对边来说,所有边都遍历一遍,因此循环内总时间复杂度为 O ( E l o g V ) O(ElogV) O(ElogV),总时间复杂度为 T ( n ) = O ( ( V + E ) l o g V ) = O ( E l o g V ) T(n)=O((V+E)logV)=O(ElogV) T(n)=O((V+E)logV)=O(ElogV)
三、克鲁斯卡尔算法(Kruskal算法)
分析
- 从一个空图开始。
- 尝试一次添加一条边,始终确保所构建的保持无循环。.
- 如果我们在每一步都确定生成的图是某个最小生成树的子集,我们就完成了。
与Prim的算法生长一棵树不同,Kruskal的算法生长一组树(森林)。
最初,这个森林只由顶点组成(没有边)。
在每一步中,添加不产生循环的权重最小的边。
继续直到森林“合并”成一棵树。
本质上,也是继承于一说的主算法:
设A为Kruskal算法选择的边集,设(u, v)为下一步要添加的边。这足以说明这一点:
t h e r e there there i s is is a a a c u t cut cut t h a t that that r e s p e c t s respects respects A A A
( u , v ) (u, v) (u,v) i s is is t h e the the l i g h t light light e d g e edge edge c r o s s i n g crossing crossing t h i s this this c u t cut cut
算法流程
- 刚开始 A A A为空集, F F F存入所有边并且从小到大排序,
- 在F中选择一条权值最小的边e,检查将e加到A上是否形成一个循环。
构成循环,则从F移除
不构成循环,则从F添加进A - F为空集时停止操作
现在有个问题,怎么才能不形成环呢,
在框架算法的每一步中, ( V , A ) (V,A) (V,A)都是非循环的,因此它是一个森林,一个顶点延申两条枝干,且枝干之间没有路径,这样就是森林。因此:
如果 u u u和 v v v在同一棵树中,则将边 u , v {u,v} u,v添加到A中创建一个循环。
如果 u u u和 v v v不在同一棵树中,那么将边 u , v {u,v} u,v添加到 A A A中不会创建一个循环。
根据这个性质,如果一条边被选中,它的两个端点若在一个树上,那么再将这条边添加进树时,肯定会形成环,根据这一性质,我们可以维护并查集去判断是否成环
并查集-Find-set
本质上,并查集就是一个个树集合,每个元素都唯一指向它的父亲,根节点父亲就是子集,因此每棵树的唯一标识就是根节点。如果两个元素唯一标识一样,那它们就在一棵树上。
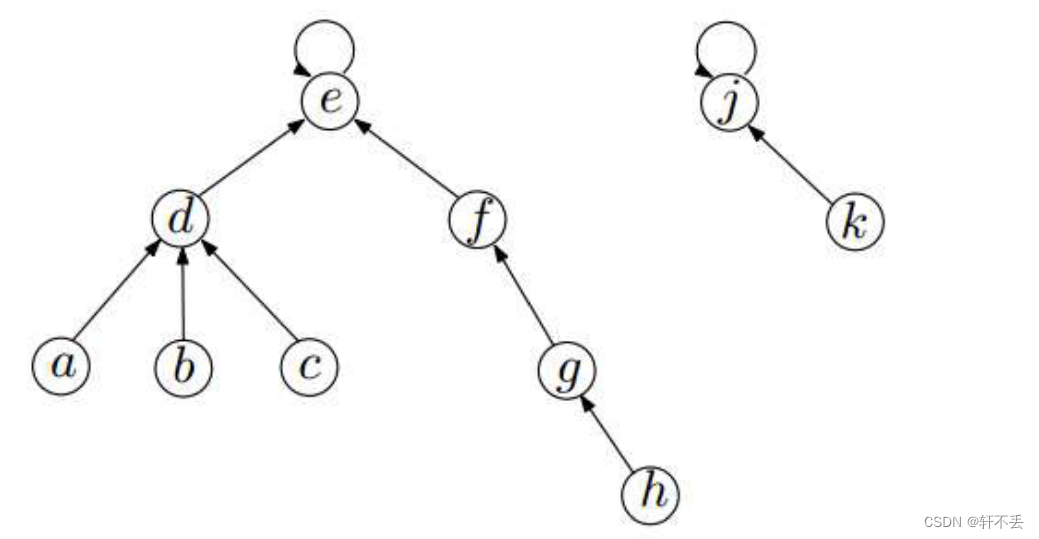
j u d g e judge judge f i n d − s e t ( u ) find-set(u) find−set(u) = = == == f i n d − s e t ( v ) find-set(v) find−set(v),维护 f i n d − s e t find-set find−set过程如下:
- C r e a t e − s e t u ) Create-set u) Create−setu):创建包含单个元素 u u u的集合。 O ( 1 ) O(1) O(1)
x.parent ← x
- F i n d − s e t ( u ) Find-set (u) Find−set(u):查找包含元素u的集合(假设每个集合都有唯一的ID,后面可知是树的根节点)。 O ( l o g n ) O(logn) O(logn)
while x != x.parent dox ← x.parent
end
- U n i o n ( u , v ) Union(u, v) Union(u,v):将分别包含u和v的集合归并为一个公共集合。(当判断完不会形成环后,可以合并). O ( l o g n ) O(logn) O(logn)(找树的根节点费时,其他都是 O ( 1 ) O(1) O(1)时间)
注意当我们将两棵树合并在一起时,我们总是将高树的根作为矮树的父树。不然会很畸形,费时。
如果两棵树有相同的高度,我们选择第一棵树的根指向第二棵树的根。树的高度增加了1(根节点+被合并的子树,因此高度+1)。其他情况下树的高度都是不变的。
a ← Find-Set(x)
b ← Find-Set(y)
if a.height <= b.height thenif a.height is equal to b.height thenb.hright++;enda.parent ← b
end
elseb.parent ← a
end
伪代码
sort E in increasing order by weight w;
A ← {}
for u ∈ V doCreate-Set(u);
end
for ei ∈E do //ei两个端点为ui,viif(find-set(ui)!=find-set(vi)) thenadd {ui,vi} to AUnion(ui,vi)end
end
return
时间复杂度分析
排序用时 O ( E l o g E ) O(ElogE) O(ElogE), c r e a t e − s e t create-set create−set用时 O ( V ) O(V) O(V),循环次数是边的次数 E E E,每次循环 u n i o n union union花费 l o g ( V ) log(V) log(V),总时间复杂度 O ( E l o g V ) O(ElogV) O(ElogV),因此总花费 T ( n ) = O ( E l o g E ) T(n)=O(ElogE) T(n)=O(ElogE)(边比顶点多,取大的)
这篇关于U4_2:图论之MST/Prim/Kruskal的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!