本文主要是介绍【CFD理论】对流项-05-非结构化网格,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
【CFD理论】对流项-05
- Unstructured Grids
- discretisation in unstructured grids 非结构化网格离散
- discretisation of the diffusion term
- Discretisation of the convective term
- linear upwind differencing
- TVD schmes in unstructured grids
Unstructured Grids
discretisation in unstructured grids 非结构化网格离散
∫ C V ∂ ∂ t d V + ∫ C V d i v ( ρ ϕ u ) d V = ∫ C V d i v ( Γ g r a d ϕ ) d V + ∫ C V S ϕ d V \int_{CV}\frac{\partial}{\partial t}dV+\int_{CV}div(\rho \phi \boldsymbol u)dV=\int_{CV}div(\Gamma \ grad \ \phi)dV+\int_{CV}S_{\phi}dV ∫CV∂t∂dV+∫CVdiv(ρϕu)dV=∫CVdiv(Γ grad ϕ)dV+∫CVSϕdV
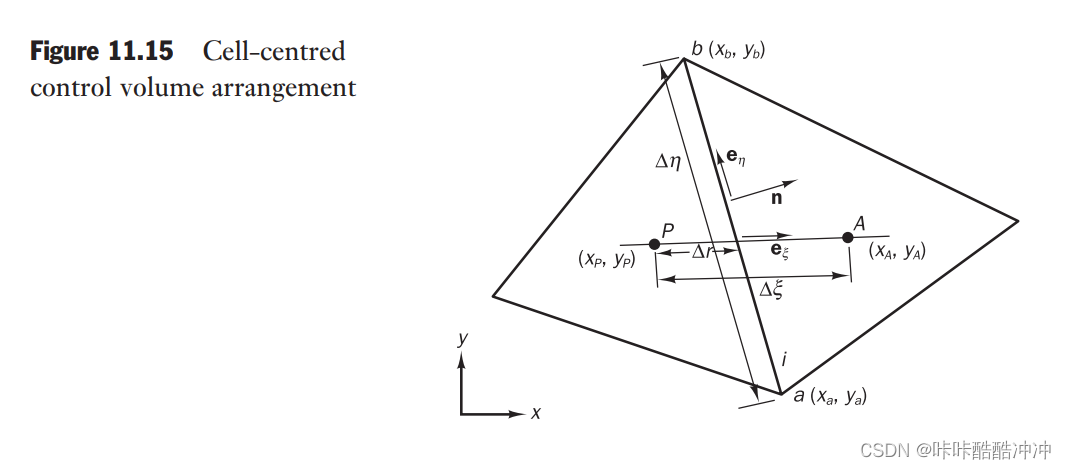
n , e η \boldsymbol {n,e_{\eta}} n,eη分别是指向面外的法向和切向矢量
P A = x A − x P y A − y P \boldsymbol {PA}=\begin{matrix} x_A-x_P \\ y_A-y_P \end{matrix}\quad PA=xA−xPyA−yP
a b = x b − x a y b − y a \boldsymbol {ab}=\begin{matrix} x_b-x_a \\ y_b-y_a \end{matrix}\quad ab=xb−xayb−ya
e ξ = P A ∣ P A ∣ \boldsymbol {e_\xi}=\frac{\boldsymbol {PA}}{|\boldsymbol {PA}|} eξ=∣PA∣PA
e η = a b ∣ a b ∣ \boldsymbol {e_\eta}=\frac{\boldsymbol {ab}}{|\boldsymbol {ab}|} eη=∣ab∣ab
Δ ξ = ∣ P A ∣ \Delta \xi=|\boldsymbol {PA}| Δξ=∣PA∣
Δ η = ∣ a b ∣ \Delta \eta=|\boldsymbol {ab}| Δη=∣ab∣
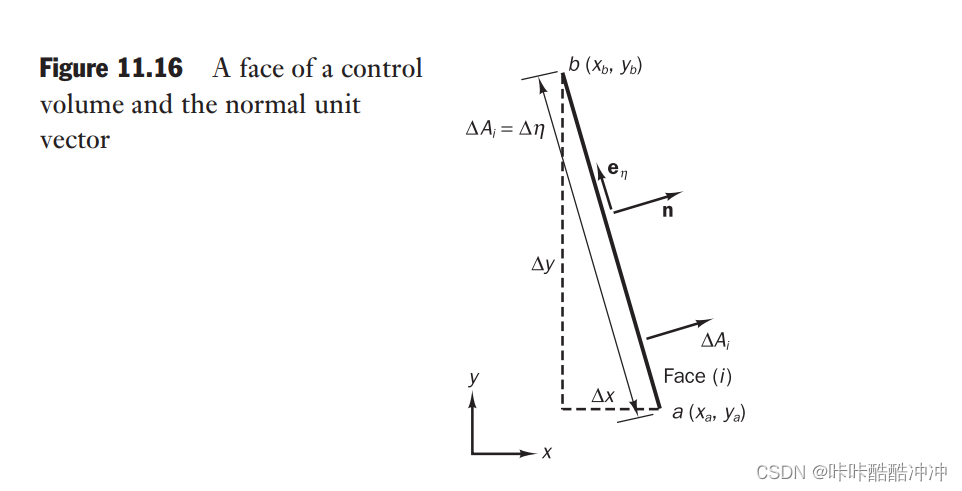
面i的面积 Δ A i \Delta A_i ΔAi
Δ A i = Δ x 2 + Δ y 2 \Delta A_i=\sqrt{\Delta x^2+\Delta y^2} ΔAi=Δx2+Δy2
面的单元法向量 n \boldsymbol n n
n = Δ y Δ A i , Δ x Δ A i \boldsymbol n=\begin{matrix} \frac{\Delta y}{\Delta A_i} , \frac{\Delta x}{\Delta A_i} \end{matrix}\quad n=ΔAiΔy,ΔAiΔx
discretisation of the diffusion term
扩散项离散,中心差分
∫ Δ A i ( Γ g r a d ϕ ) ⋅ n d A ≈ Γ g r a d ϕ ⋅ n i Δ A i ≈ Γ ( ϕ A − ϕ P Δ ξ ) Δ A i \int_{\Delta A_i}(\Gamma grad\phi)\cdot \boldsymbol n dA\approx\Gamma grad\phi\cdot\boldsymbol n_i\Delta A_i\approx\Gamma(\frac{\phi_A-\phi_P}{\Delta \xi})\Delta A_i ∫ΔAi(Γgradϕ)⋅ndA≈Γgradϕ⋅niΔAi≈Γ(ΔξϕA−ϕP)ΔAi
之前的形式
∫ f ( Γ Δ ϕ ) ⋅ d S = ( Γ Δ ϕ ) f ⋅ n f S f = Γ ( ϕ E − ϕ P Δ x ) f S f \int_f(\Gamma\Delta\phi)\cdot d\boldsymbol S=(\Gamma\Delta \phi)_f\cdot \boldsymbol n_fS_f=\Gamma(\frac{\phi_E-\phi_P}{\Delta x})_f S_f ∫f(ΓΔϕ)⋅dS=(ΓΔϕ)f⋅nfSf=Γ(ΔxϕE−ϕP)fSf
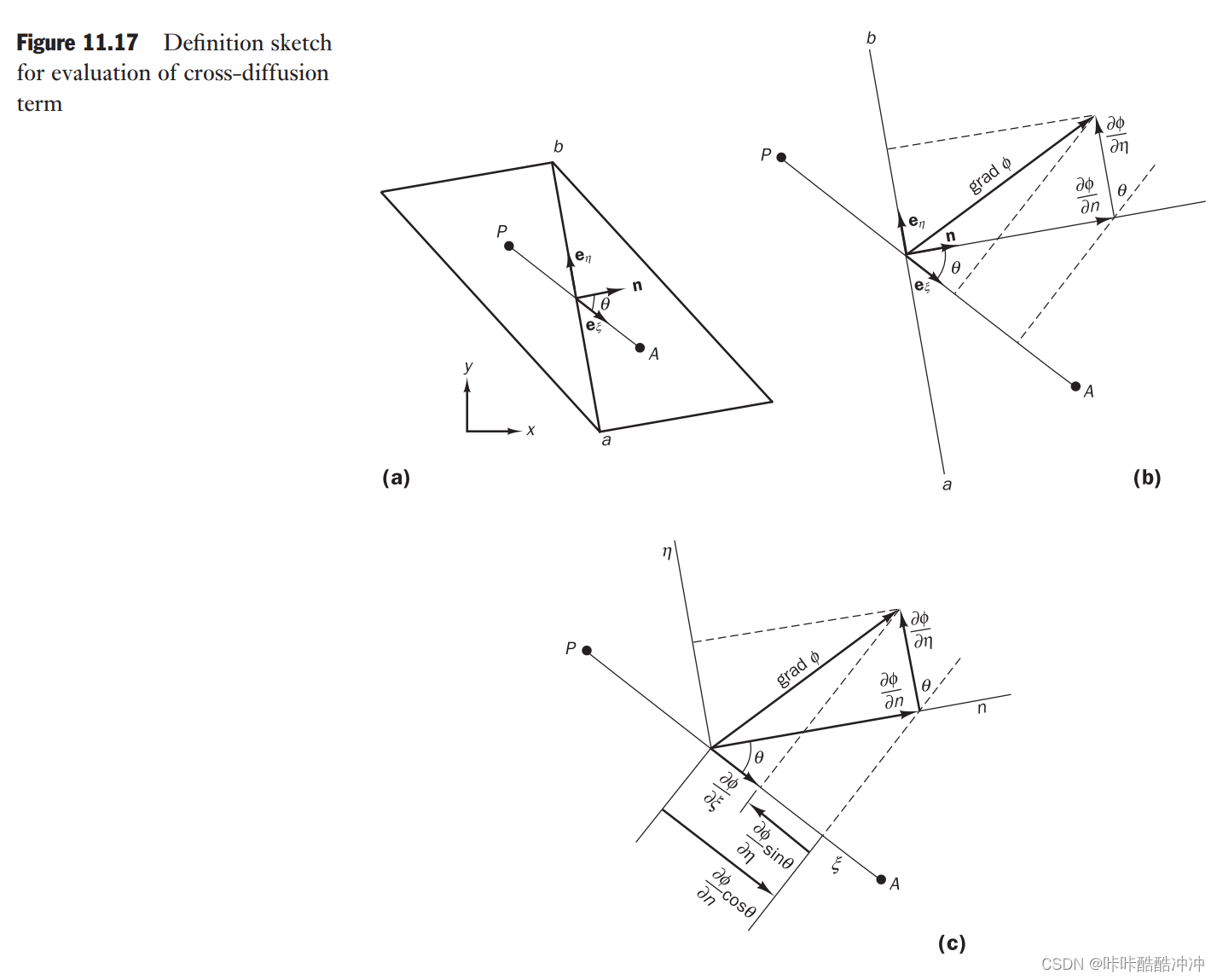
- ∂ ϕ ∂ ξ = ∂ ϕ ∂ n c o s θ − ∂ ϕ ∂ η s i n θ \frac{\partial \phi}{\partial \xi}=\frac{\partial \phi}{\partial n}cos\theta-\frac{\partial \phi}{\partial \eta}sin\theta ∂ξ∂ϕ=∂n∂ϕcosθ−∂η∂ϕsinθ
- ∇ ϕ ⋅ n = ∂ ϕ ∂ n = ∂ ϕ ∂ ξ 1 c o s θ + ∂ ϕ ∂ ξ t a n θ = g r a d ϕ ⋅ n \nabla \phi \cdot \boldsymbol n=\frac{\partial \phi}{\partial n}=\frac{\partial \phi}{\partial \xi}\frac{1}{cos\theta}+\frac{\partial \phi}{\partial \xi}tan\theta=grad\phi\cdot \boldsymbol n ∇ϕ⋅n=∂n∂ϕ=∂ξ∂ϕcosθ1+∂ξ∂ϕtanθ=gradϕ⋅n
- 非结构化网格direct gradient 中心差分
∂ ϕ ∂ ξ = ϕ A − ϕ P Δ ξ \frac{\partial \phi}{\partial \xi}=\frac{\phi_A-\phi_P}{\Delta \xi} ∂ξ∂ϕ=ΔξϕA−ϕP - 非结构化网格cross-diffusion
∂ ϕ ∂ η = ϕ b − ϕ a Δ η \frac{\partial \phi}{\partial \eta}=\frac{\phi_b-\phi_a}{\Delta \eta} ∂η∂ϕ=Δηϕb−ϕa - ∇ ϕ ⋅ n Δ A i = Δ A i ϕ A − ϕ P ∂ ξ 1 c o s θ + ∂ ϕ b − ϕ a ∂ ξ t a n θ Δ A i \nabla \phi \cdot \boldsymbol n\Delta A_i=\Delta A_i\frac{\phi_A-\phi_P}{\partial \xi}\frac{1}{cos\theta}+\frac{\partial \phi_b-\phi_a}{\partial \xi}tan\theta\Delta A_i ∇ϕ⋅nΔAi=ΔAi∂ξϕA−ϕPcosθ1+∂ξ∂ϕb−ϕatanθΔAi
1 c o s θ = 1 n ⋅ e x i = n ⋅ n n ⋅ e ξ \frac{1}{cos\theta}=\frac{1}{\boldsymbol n\cdot\boldsymbol e_{xi}}=\frac{\boldsymbol n\cdot \boldsymbol n}{\boldsymbol n\cdot \boldsymbol e_{\xi}} cosθ1=n⋅exi1=n⋅eξn⋅n
t a n θ = 1 n ⋅ e x i = − e ξ ⋅ e η n ⋅ e ξ tan\theta=\frac{1}{\boldsymbol n\cdot\boldsymbol e_{xi}}=-\frac{\boldsymbol e_\xi \cdot \boldsymbol e_\eta}{\boldsymbol n\cdot \boldsymbol e_{\xi}} tanθ=n⋅exi1=−n⋅eξeξ⋅eη - ∇ ϕ ⋅ n Δ A i = Δ A i ϕ A − ϕ P ∂ ξ n ⋅ n n ⋅ e ξ − ∂ ϕ b − ϕ a ∂ η e ξ ⋅ e η n ⋅ e ξ Δ A i \nabla \phi \cdot \boldsymbol n\Delta A_i=\Delta A_i\frac{\phi_A-\phi_P}{\partial \xi}\frac{\boldsymbol n\cdot \boldsymbol n}{\boldsymbol n\cdot \boldsymbol e_{\xi}}-\frac{\partial \phi_b-\phi_a}{\partial \eta}\frac{\boldsymbol e_\xi \cdot \boldsymbol e_\eta}{\boldsymbol n\cdot \boldsymbol e_{\xi}}\Delta A_i ∇ϕ⋅nΔAi=ΔAi∂ξϕA−ϕPn⋅eξn⋅n−∂η∂ϕb−ϕan⋅eξeξ⋅eηΔAi
- ∇ ϕ ⋅ n Δ A i = Δ A i ϕ A − ϕ P ∂ ξ n ⋅ n n ⋅ e ξ + S D − c r o s s \nabla \phi \cdot \boldsymbol n\Delta A_i=\Delta A_i\frac{\phi_A-\phi_P}{\partial \xi}\frac{\boldsymbol n\cdot \boldsymbol n}{\boldsymbol n\cdot \boldsymbol e_{\xi}}+S_{D-cross} ∇ϕ⋅nΔAi=ΔAi∂ξϕA−ϕPn⋅eξn⋅n+SD−cross
Discretisation of the convective term
∑ f ∫ f ρ ϕ U ⋅ d S = ∑ f ∫ Δ A i ρ ϕ u ⋅ n d A = ∑ f ( ρ ϕ u ) f ⋅ n A f \sum_f\int_f\rho\phi U\cdot d\boldsymbol S=\sum_f\int_{\Delta A_i}\rho\phi \boldsymbol u\cdot \boldsymbol n dA=\sum_f(\rho \phi\boldsymbol u)_f\cdot \boldsymbol n A_f ∑f∫fρϕU⋅dS=∑f∫ΔAiρϕu⋅ndA=∑f(ρϕu)f⋅nAf
linear upwind differencing
ϕ e = ϕ P + ϕ P − ϕ W Δ x 1 2 Δ x \phi_e=\phi_P+\frac{\phi_P-\phi_W}{\Delta x}\frac{1}{2}\Delta x ϕe=ϕP+ΔxϕP−ϕW21Δx
对于非结构化网格可以使用泰勒展开式将 ϕ \phi ϕ
ϕ ( x , y ) = ϕ P + ( ∇ ϕ ) P ⋅ Δ r + O ( Δ r ) 2 \phi(x,y)=\phi_P+(\nabla\phi)_P\cdot\Delta \boldsymbol r+\mathcal{O}(\Delta \boldsymbol r)^2 ϕ(x,y)=ϕP+(∇ϕ)P⋅Δr+O(Δr)2
如果是 Δ r \Delta \boldsymbol r Δr是点P到面心的距离
ϕ i = ϕ P + ( ∇ ϕ ) P ⋅ Δ r \phi_i=\phi_P+(\nabla \phi)_P \cdot \Delta \boldsymbol r ϕi=ϕP+(∇ϕ)P⋅Δr
⇒ \Rightarrow ⇒
- 对于非结构化网格,需要 面心值 ϕ i \color{red}面心值\phi_i 面心值ϕi,就必须要知道 体心梯度 ( ∇ ϕ ) P \color{red}体心梯度(\nabla \phi)_P 体心梯度(∇ϕ)P
- 最小二乘法 重构 r e c o n s t r u c t \color{red} 重构reconstruct 重构reconstruct体心梯度
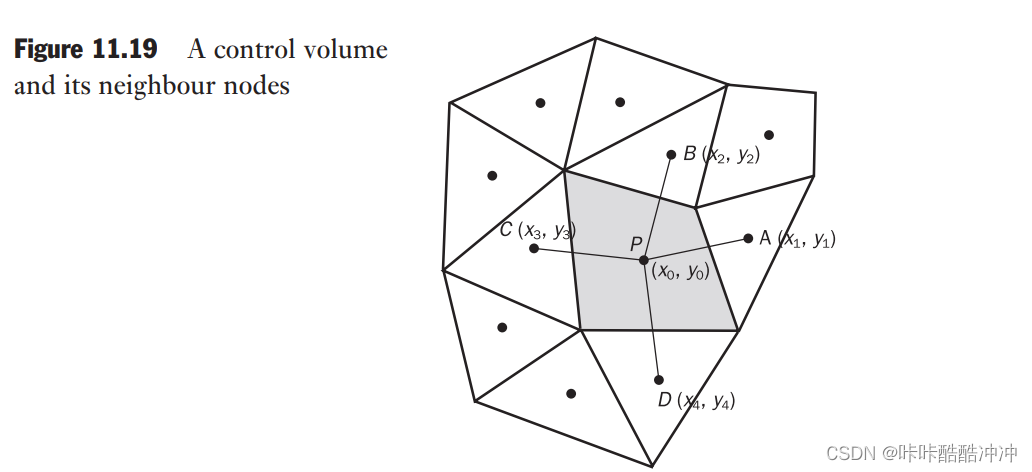
ϕ 1 − ϕ 0 = ( ∂ ϕ ∂ x ) ∣ 0 Δ x 1 + ( ∂ ϕ ∂ y ) ∣ 0 Δ y 1 ϕ 2 − ϕ 0 = ( ∂ ϕ ∂ x ) ∣ 0 Δ x 2 + ( ∂ ϕ ∂ y ) ∣ 0 Δ y 2 ϕ 3 − ϕ 0 = ( ∂ ϕ ∂ x ) ∣ 0 Δ x 3 + ( ∂ ϕ ∂ y ) ∣ 0 Δ y 3 ϕ 4 − ϕ 0 = ( ∂ ϕ ∂ x ) ∣ 0 Δ x 4 + ( ∂ ϕ ∂ y ) ∣ 0 Δ y 4 \phi_1-\phi_0=(\frac{\partial \phi}{\partial x})|_0\Delta x_1+(\frac{\partial \phi}{\partial y})|_0\Delta y_1\\ \phi_2-\phi_0=(\frac{\partial \phi}{\partial x})|_0\Delta x_2+(\frac{\partial \phi}{\partial y})|_0\Delta y_2\\ \phi_3-\phi_0=(\frac{\partial \phi}{\partial x})|_0\Delta x_3+(\frac{\partial \phi}{\partial y})|_0\Delta y_3\\ \phi_4-\phi_0=(\frac{\partial \phi}{\partial x})|_0\Delta x_4+(\frac{\partial \phi}{\partial y})|_0\Delta y_4\\ ϕ1−ϕ0=(∂x∂ϕ)∣0Δx1+(∂y∂ϕ)∣0Δy1ϕ2−ϕ0=(∂x∂ϕ)∣0Δx2+(∂y∂ϕ)∣0Δy2ϕ3−ϕ0=(∂x∂ϕ)∣0Δx3+(∂y∂ϕ)∣0Δy3ϕ4−ϕ0=(∂x∂ϕ)∣0Δx4+(∂y∂ϕ)∣0Δy4
矩阵形式
[ Δ x 1 Δ y 1 Δ x 2 Δ y 2 Δ x 3 Δ y 3 . . . . . . Δ x N Δ y N ] [ Δ ( ∂ ϕ ∂ x ) ∣ 0 Δ ( ∂ ϕ ∂ y ) ∣ 0 ] = [ ϕ 1 − ϕ 0 ϕ 2 − ϕ 0 ϕ 3 − ϕ 0 . . . ϕ N − ϕ 0 ] \begin{bmatrix} \Delta x_1&\Delta y_1\\ \Delta x_2&\Delta y_2\\ \Delta x_3&\Delta y_3\\ ...&...\\ \Delta x_N&\Delta y_N\\ \end{bmatrix} \begin{bmatrix} \Delta (\frac{\partial \phi}{\partial x})|_0\\ \Delta (\frac{\partial \phi}{\partial y})|_0\\ \end{bmatrix} = \begin{bmatrix} \phi_1-\phi_0\\ \phi_2-\phi_0\\ \phi_3-\phi_0\\ ...\\ \phi_N-\phi_0\\ \end{bmatrix} ⎣ ⎡Δx1Δx2Δx3...ΔxNΔy1Δy2Δy3...ΔyN⎦ ⎤[Δ(∂x∂ϕ)∣0Δ(∂y∂ϕ)∣0]=⎣ ⎡ϕ1−ϕ0ϕ2−ϕ0ϕ3−ϕ0...ϕN−ϕ0⎦ ⎤
矩阵 超定 o v e r d e t e r m i n d \color{red}超定 overdetermind 超定overdetermind,所以不太可能直接求解
需要用 最小二乘法 \color{red}最小二乘法 最小二乘法
A T A x = A T b x = ( A T A ) − 1 A T b \boldsymbol{A^TAx=A^Tb}\\ \boldsymbol{x=(A^TA)^{-1}A^Tb} ATAx=ATbx=(ATA)−1ATb
TVD schmes in unstructured grids
- 结构化网格的TVD
ϕ i = ϕ P + ψ ( r ) 2 ( ϕ E − ϕ P ) r = ϕ P − ϕ W ϕ E − ϕ P \phi_i=\phi_P+\frac{\psi(r)}{2}(\phi_E-\phi_P)\\ r=\frac{\phi_P-\phi_W}{\phi_E-\phi_P} ϕi=ϕP+2ψ(r)(ϕE−ϕP)r=ϕE−ϕPϕP−ϕW
在非结构化网格中,上游点 W 很难确定,所以需要构造一个假的点 B \color{red}在非结构化网格中,上游点W很难确定,所以需要构造一个假的点B 在非结构化网格中,上游点W很难确定,所以需要构造一个假的点B
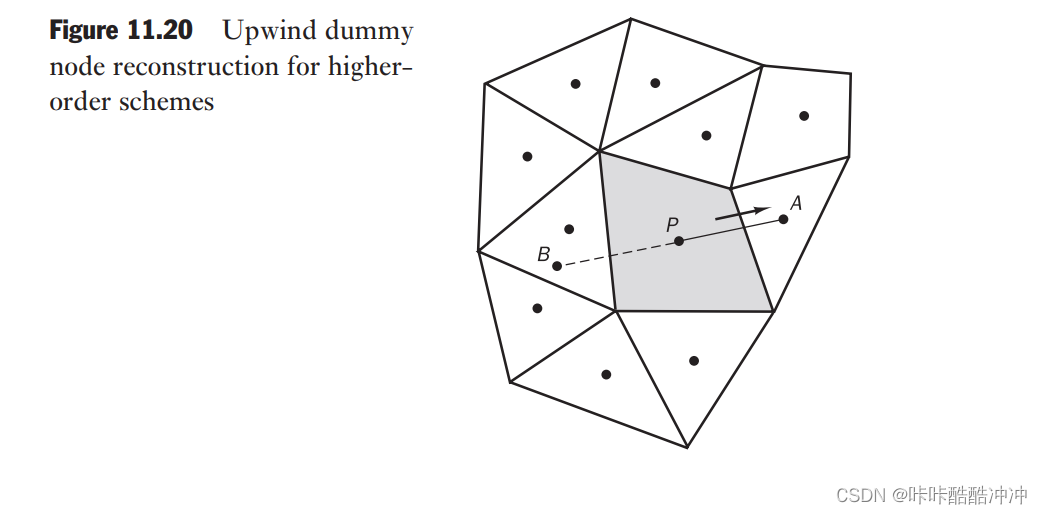
- 在非结构化网格TVD
r = 2 ( ∇ ϕ ) P ⋅ r P A ϕ D − ϕ U − 1 r=\frac{2(\nabla \phi)_P\cdot \boldsymbol r_{PA}}{\phi_D-\phi_U}-1 r=ϕD−ϕU2(∇ϕ)P⋅rPA−1
对流通量TVD表达式变为
ϕ i = ϕ U = ψ ( r ) 2 ( ϕ D − ϕ U ) ψ ( r ) = 0.25 r + 0.75 ( Q U I C K ) ( ∇ ϕ ) p 最小二乘法求得 ϕ D 下游, ϕ U 上游 \phi_i=\phi_U=\frac{\psi(r)}{2}(\phi_D-\phi_U)\\ \psi(r)=0.25r+0.75(QUICK)\\ (\nabla \phi)_p最小二乘法求得\\ \phi_D下游,\phi_U上游 ϕi=ϕU=2ψ(r)(ϕD−ϕU)ψ(r)=0.25r+0.75(QUICK)(∇ϕ)p最小二乘法求得ϕD下游,ϕU上游
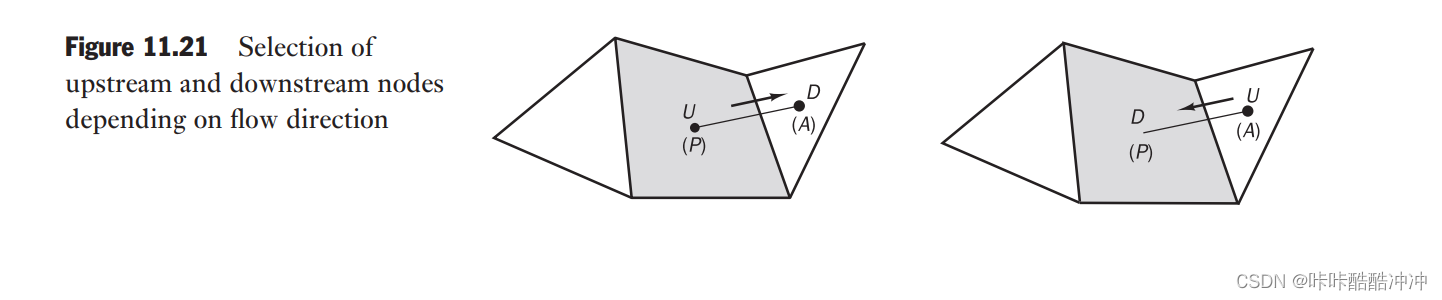
这篇关于【CFD理论】对流项-05-非结构化网格的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









