HNUST-OJ -1963-邻接矩阵表示法

目录

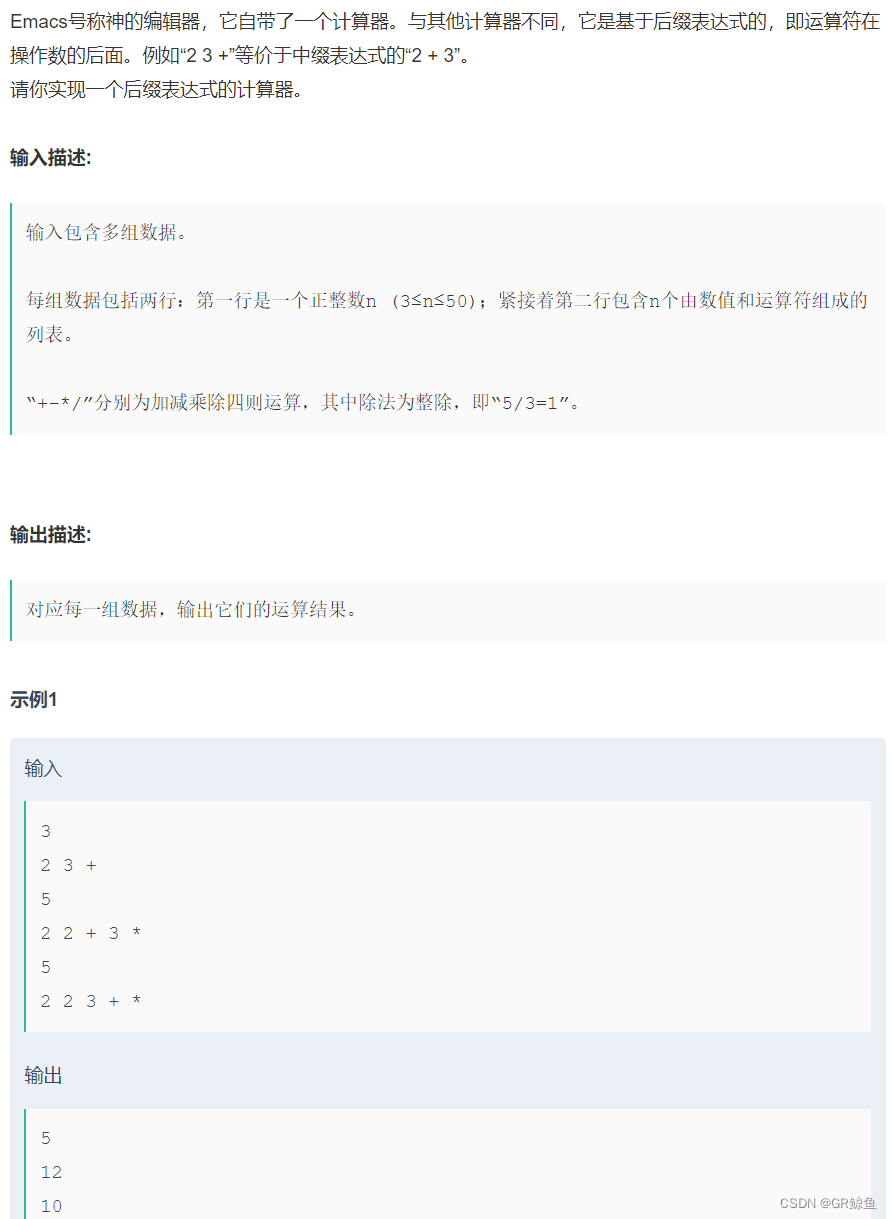
原题复刻：

思想的火花：

代码复刻：

原题复刻：

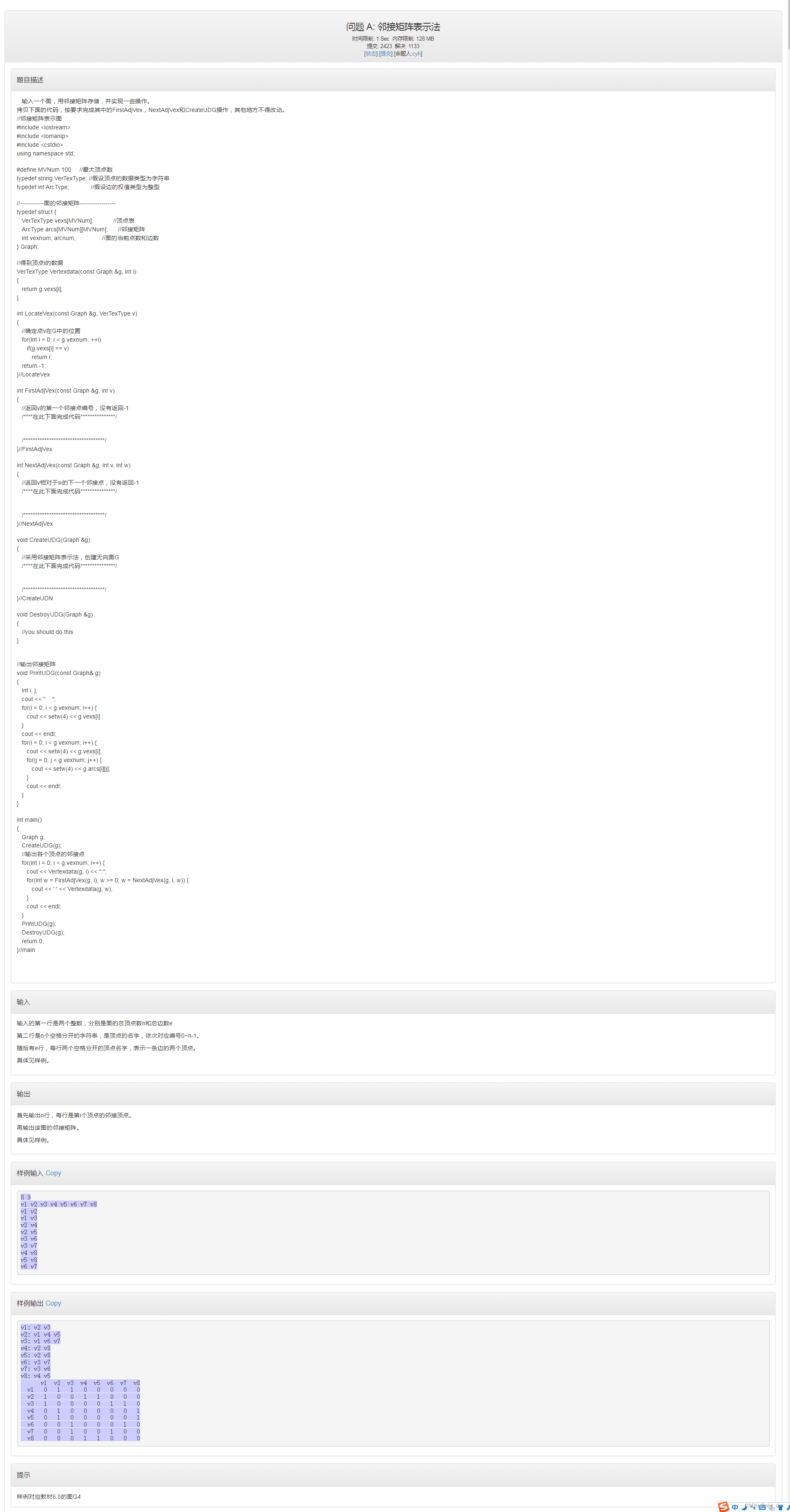
思想的火花：

1.Graph结构体

{

VerTexType vexs[MVNum];//顶点表（人话就是用来存顶点有哪些）

ArcType arcs[MVNum][MVNum];//邻接矩阵（人话就是用矩阵来表示边的关系，有为1，无为零）

int vexnum, arcnum;//顶点和边的个数

}

2.LocateVex(const Graph &g, VerTexType v)

{

就是从顶点表中找到v的位置

}

3.FirstAdjVex(const Graph &g, int v)

{

返回顶点v的第一个邻接点编号，没有返回-1

}

4.NextAdjVex(const Graph &g, int v, int w)
{
    就是寻找邻接矩阵中与顶点v有边的，除w之外的另一个节点是谁，没有返回-1
}

5.CreateUDG(Graph &g)
{
    cin>>g.vexnum>>g.arcnum;//顶点个数
    for(int  i=0; i<g.vexnum; i++)cin>>g.vexs[i];//往顶点表中存顶点
    while(g.arcnum--)//不建议直接减掉，但本题再也没有用过边的个数，就简便点
    {
        string x1,x2;
        cin>>x1>>x2;
        int m=LocateVex(g,x1),n=LocateVex(g,x2);//定位新出现的边关系中的两个顶点x1和x2在顶点表中的位置，方便建立邻接矩阵。
        if(m!=-1&&n!=-1)g.arcs[m][n]=g.arcs[n][m]=1;//此处加入if防止有顶点不存在从而越界
    }
}

6.DestroyUDG(Graph &g)

{

memset(g.arcs,0,sizeof(g.arcs));//此处的摧毁理解为重置邻接矩阵

}

7.PrintUDG(const Graph& g)

{

就是把邻接矩阵按格式打印出来 

}

代码复刻：

#include<bits/stdc++.h>
using namespace std;#define MVNum 100     //最大顶点数
typedef string VerTexType; //假设顶点的数据类型为字符串
typedef int ArcType;             //假设边的权值类型为整型//------------图的邻接矩阵------------------
typedef struct
{VerTexType vexs[MVNum];            //顶点表,用以存储顶点ArcType arcs[MVNum][MVNum];      //邻接矩阵int vexnum, arcnum;                //图的当前点数和边数
} Graph;
int LocateVex(const Graph &g, VerTexType v)
{//确定点v在G中顶点表的位置for(int i = 0; i < g.vexnum; ++i)if(g.vexs[i] == v)return i;return -1;
}//LocateVexint FirstAdjVex(const Graph &g, int v)
{//返回顶点v的第一个邻接点编号，没有返回-1/****在此下面完成代码***************/for(int i=0; i<g.vexnum; i++)if(g.arcs[v][i])return i;return -1;/***********************************/
}//FirstAdjVexint NextAdjVex(const Graph &g, int v, int w)
{//返回顶点v相对于w的下一个邻接点，没有返回-1/****在此下面完成代码***************/for(int i=w+1; i<g.vexnum; i++)if(g.arcs[v][i])return i;return -1;/***********************************/
}//NextAdjVexvoid CreateUDG(Graph &g)
{//采用邻接矩阵表示法，创建无向图G/****在此下面完成代码***************/cin>>g.vexnum>>g.arcnum;for(int  i=0; i<g.vexnum; i++)cin>>g.vexs[i];while(g.arcnum--){string x1,x2;cin>>x1>>x2;int m=LocateVex(g,x1),n=LocateVex(g,x2);if(m!=-1&&n!=-1)g.arcs[m][n]=g.arcs[n][m]=1;}/***********************************/
}//CreateUDNvoid DestroyUDG(Graph &g)
{memset(g.arcs,0,sizeof(g.arcs));
}//输出邻接矩阵
void PrintUDG(const Graph& g)
{int i, j;cout << "    ";for(i = 0; i < g.vexnum; i++){cout << setw(4) << g.vexs[i] ;}cout << endl;for(i = 0; i < g.vexnum; i++){cout << setw(4) << g.vexs[i];for(j = 0; j < g.vexnum; j++){cout << setw(4) << g.arcs[i][j];}cout << endl;}
}int main()
{Graph g;CreateUDG(g);//输出各个顶点的邻接点for(int i = 0; i < g.vexnum; i++){cout << g.vexs[i] << ":";for(int w = FirstAdjVex(g, i); w >= 0; w = NextAdjVex(g, i, w)){cout << ' ' << g.vexs[w];}cout << endl;}PrintUDG(g);DestroyUDG(g);return 0;
}//main