RWD安全估计算法的仿真过程及思考

算法思考

为什么要进行窗口长度的取平均？

直观的思考，叠加的攻击也是一个零均值的噪声过程，这个过程可以隐匿在量测噪声中，如果攻击与噪声发生的叠加，是同向叠加，就会产生破坏效果；而若反向叠加，一定程度上会互相抵消，甚至没有攻击效果。
窗口长度取平均就是在用统计的方式入手，对这种叠加产生的期望值的偏移进行检测，这样可以检测出不能观察到的“上下震动”式的偏移。

随机变量不相关的前提下，叠加后的方差=各方差的和

因此隐匿攻击的情况下，比如文章设置的量测噪声标准差=攻击标准差=1.1的情况下，叠加后的带攻击量测噪声的标准差是发生变化的，方差=噪声方差+攻击方差。因此分布会发生变化，RWD算法和NRD算法都能进行检出。

恢复算法为什么要如此设计？

恢复算法：
正常Kalman过程
上一时刻量测值的估计值
$${\hat{z}}_{k-1}=H{\hat{x}}_{k-1}$$
Kalman
$$\begin{gathered} {P}_k^{-}=A{P}_{k-1}{A}^T+Q \\ {\hat{x}}_k^{-}=A{\hat{x}}_{k-1} \\ {K}_k=P_k^{-}{H}^T(H{P}_k^{-}{H}^T+R{)}^{-1} \\ {\hat{x}}_k={\hat{x}}_k^{-}+K_k(z_k-H{\hat{x}}_k^{-}) \\ {P}_k=(I-KH)P_k^{-} \end{gathered}$$
恢复过程，将
$$\cancel{{\hat{x}}_k={\hat{x}}_k^{-}+K_k(z_k-H{\hat{x}}_k^{-})}$$
更换为
$$\begin{gathered} {\hat{x}}_k={\hat{x}}_k^{-}+K_k({\hat{z}}_{k-1}-H{\hat{x}}_k^{-}) \\ ={\hat{x}}_k^{-}+K_k(H{\hat{x}}_{k-1}-H{\hat{x}}_k^{-}) \\ ={\hat{x}}_k^{-}+K_{k}H({\hat{x}}_{k-1}-{\hat{x}}_k^{-}) \\ =A{\hat{x}}_{k-1}+K_{k}H({\hat{x}}_{k-1}-A{\hat{x}}_{k-1}) \\ =A{\hat{x}}_{k-1}+K_{k}H(I-A){\hat{x}}_{k-1} \end{gathered}$$
在我们的仿真背景下，$H=I$
$${\hat{x}}_k=A{\hat{x}}_{k-1}+K_k(I-A){\hat{x}}_{k-1}$$
这里面${\hat{x}}_k^{-}$是带着状态方程的信息的，相当于是利用模型的信息进行的预测更新，我原本的想法是既然发现了攻击，就相当于量测可以认为已经没有信息量了，所以直接用${\hat{x}}_k^{-}$去代替${\hat{x}}_k$，等于是不进行量测更新，即
$${\hat{x}}_k={\hat{x}}_k^{-}=A{\hat{x}}_{k-1}$$
但本文作者在${\hat{x}}_k^{-}$的基础上又加了一个$H({\hat{x}}_{k-1}-{\hat{x}}_k^{-})$的量，从原始逻辑来看是用上一时刻更为精准的量测值来替代这一时刻的受攻击的量测值，但是上一时刻量测值对于这一时刻完全没有信息量，确实没有必要加入。
本文多加的$K_k(I-A){\hat{x}}_{k-1}$这个量，$K_k$是正定的，如果
1、$A=I$，也就是在本仿真背景下系统参数稳定不变（这也是这篇文章的假设背景），$I-A=0$，则文章设置的恢复算法其实就是${\hat{x}}_k={\hat{x}}_k^{-}=A{\hat{x}}_{k-1}$，二者完全一致。

2、$A>I$，也就是在本仿真背景下系统参数呈现递增趋势，$I-A<0$，则恢复后的${\hat{x}}_k$式子实际上是带着对时间更新${\hat{x}}_k^{-}$的削弱。在实际仿真debug中，对检出攻击时刻的${\hat{z}}_{k-1}-H{\hat{x}}_k^{-}$进行计算也发现${\hat{z}}_{k-1}-H{\hat{x}}_k^{-}<0$，这也印证了前面的推导。

同时由于本文使用的是定常系统，$I-A$为固定值，滤波器进入稳态之后，$K_k$也是固定值，因此上面所说的削弱量就取决于${\hat{x}}_{k-1}$，由于假设系统状态值缓慢上升，则${\hat{x}}_{k-1}$缓慢增加，因此削弱量缓慢增加，在长时间故障的时间段内，本文恢复算法始终是在预测估计值基础上削减一个缓慢增加的值，而且由于系统矩阵A设置的非常小$（1,0;0,1.01）$，增加的非常缓慢，因此直观来看，就是比直接使用预测估计值始终小一个常数。

显然这样误差是更大的。

3、$A<I$，也就是在本仿真背景下系统参数呈现递增趋势，$I-A>0$，在实际仿真debug中，对检出攻击时刻的${\hat{z}}_{k-1}-H{\hat{x}}_k^{-}$进行计算也发现${\hat{z}}_{k-1}-H{\hat{x}}_k^{-}>0$，这也印证了前面的推导。即在递增的设置下，会在预测估计值上增加一个缓慢减小的值。

因此得出结论：本文恢复算法对变化的系统适应性不好，且没有优点。
在后面代码中可以将

xkf1RWD(:,k)=xbup1+K1*(z1back-H1*xbup1);

和

xkf2RWD(:,k)=xbup2+K2*(z2back-H2*xbup2);

直接改为

xkf1RWD(:,k)=xbup1;

和

xkf2RWD(:,k)=xbup2;

仿真背景

模型设置

为了简单，使用一个不相关双通道两传感器的模型，两个传感器每时刻独立地观测两个状态量，并进行融合。
RWD算法的使用背景为智能电网，电网中的参数变化缓慢，一般可以认为是稳定系统，因此设定状态转移矩阵A为单位矩阵，系统参数波动仅由噪声引起。

攻击设置

我们设置第2个传感器受到攻击，第1个传感器不受攻击。

攻击发生在30 ~ 50 和 70 ~ 90时刻。

同时为了考量虚警和漏警，我们进行多次重复试验。

依照文献设置，分为三种情况：
1、隐匿攻击
设置攻击功率（标准差）=量测噪声功率（标准差）=1.1
2、非隐匿攻击
设置攻击功率（标准差）=2.6
量测噪声功率（标准差）=1.1
3、极端非隐匿攻击
设置攻击功率（标准差）=5
量测噪声功率（标准差）=0.1

代码

%Project: 不相关&双通道&二维&滚动窗检测器
%Author: Jace
%Data: 2021/09/15
%--------------------准备---------------------
close all;
clear all;
clc;
%------------------初始化参数---------------------N=100;%设定采样点数，即持续时长%攻击检测相关参数
T=20;%设定滚动窗口长度
H=0.6;%检测阈值S1=zeros(1,N);%检测量
S2=zeros(1,N);%检测量%噪声相关参数
P0=0.01;%初始状态噪声协方差
Q=[0.01,0.0;0.0,0.01];%设定系统噪声
R1=1.1;%设定局部观测1噪声
R2=1.1;%设定局部观测2噪声
w=sqrt(Q)*randn(2,N);
v1=sqrt(R1)*randn(1,N);
v2=sqrt(R2)*randn(1,N);%攻击相关参数
attack1=0;%攻击1是否开启
attack2=1;%攻击2是否开启atk1=sqrt(R1)*randn(1,N);%隐匿攻击1
atk2=sqrt(R2)*randn(1,N);%隐匿攻击2，通过设置此处来变更攻击类型%系统模型参数
A=[1,0;0,1];%状态转移矩阵
H1=[1,0];%局部量测1量测矩阵
H2=[0,1];%局部量测2量测矩阵%----------------初始化分配空间-------------------------
%真实状态值初始化
x=zeros(2,N);%物体真实状态值（分配空间），2*N维矩阵
x(:,1)=[10+P0*randn(1);20+P0*randn(1)];%物体初始真实状态值%误差协方差初始化
p1=[1,0;0,1];%局部滤波1误差协方差初始值
p2=[1,0;0,1];%局部滤波2误差协方差初始值
p=[1,0;0,1];%全局滤波误差协方差初始值%两个传感器量测值初始化
z1=zeros(1,N);%量测值1
z1(1)=H1*x(:,1);%观测1真实值初始值,第一列的列向量取出第一行，成为标量z2=zeros(1,N);%量测值2
z2(1)=H2*x(:,1);%观测2真实值初始值,第一列的列向量取出第二行，成为标量%各滤波器估计值初始化
xkf1=zeros(2,N);%局部估计状态1
xkf1(:,1)=x(:,1);%局部估计状态1初始化为第一列的列向量xkf1RWD=zeros(2,N);%局部估计状态1备份
xkf1RWD(:,1)=xkf1(:,1);xkf2=zeros(2,N);%局部估计状态2
xkf2(:,1)=x(:,1);%局部估计状态2初始化为第一列的列向量xkf2RWD=zeros(2,N);%局部估计状态2备份
xkf2RWD(:,1)=xkf2(:,1);xkfRWD=zeros(2,N);%全局估计状态
xkfRWD(:,1)=x(:,1);%全局估计状态初始化为第一列的列向量I=eye(2);%2*2单位矩阵Alarm=zeros(2,N);
%----------------RWD------------------------
for k=2:N%系统模型x(:,k)=A*x(:,k-1)+w(k);%量测模型，标量z1(k)=H1*x(:,k)+v1(k);z2(k)=H2*x(:,k)+v2(k);%注入攻击if attack1==1if k>=30&&k<=50||k>=70&&k<=90z1(k)=z1(k)+atk1(k);endendif attack2==1if k>=30&&k<=50||k>=70&&k<=90z2(k)=z2(k)+atk2(k);endend%----------------标准Kalman过程------------------------%估计误差协方差预测更新p_pre1=A*p1*A'+Q;p_pre2=A*p2*A'+Q;%增益矩阵预测更新K1=p_pre1*H1'/(H1*p_pre1*H1'+R1);K2=p_pre2*H2'/(H2*p_pre2*H2'+R2);%状态值预测更新x_pre1=A*xkfRWD(:,k-1);x_pre2=A*xkfRWD(:,k-1);%备份先验估计值，用于存在攻击时的状态恢复xbup1=x_pre1;xbup2=x_pre2;%状态值量测更新xkf1(:,k)=x_pre1+K1*(z1(k)-H1*x_pre1);xkf2(:,k)=x_pre2+K2*(z2(k)-H2*x_pre2);%估计误差协方差量测更新p1=(I-K1*H1)*p_pre1;p2=(I-K2*H2)*p_pre2;%局部滤波的估计值记录xkf1RWD(:,k)=xkf1(:,k);xkf2RWD(:,k)=xkf2(:,k);%----------------攻击检测RWD算法部分------------------------i=k-T+1;%计算窗口最左侧时刻i(i<1)=1;%控制初始的时候窗口不要左侧越界%求和变量清零Sigksum1=0;Sigksum2=0;%求和for t=i:kSigksum1=Sigksum1+(z1(t)-H1*xkf1RWD(:,t))*(z1(t)-H1*xkf1RWD(:,t))';%对窗口内的误差求累积和，注意这里用的是原始受攻击下的量测值和估计值Sigksum2=Sigksum2+(z2(t)-H2*xkf2RWD(:,t))*(z2(t)-H2*xkf2RWD(:,t))';end%取均值if k>T+1Sigk1=Sigksum1/T;Sigk2=Sigksum2/T;elseSigk1=Sigksum1/(k-1);Sigk2=Sigksum2/(k-1);end%计算标准Kalman的残差量协方差Sigrk1=H1*p1*H1'+R1;Sigrk2=H2*p2*H2'+R2;%攻击检测参量S1(k)=Sigk1-Sigrk1;S2(k)=Sigk2-Sigrk2;if S1(k)<0S1(k)=0;endif S2(k)<0S2(k)=0;end%----------------利用备份状态值重新估计,RWD恢复过程------------------------if S1(k)>HAlarm(1,k)=1;z1back=H1*xkf1RWD(:,k-1);%量测值回退到上一时刻的估计值%局部滤波1的重新估计（利用备份）xkf1RWD(:,k)=xbup1+K1*(z1back-H1*xbup1);end  if S2(k)>HAlarm(2,k)=1;z2back=H2*xkf2RWD(:,k-1);%量测值回退到上一时刻的估计值%局部滤波2的重新估计（利用备份）xkf2RWD(:,k)=xbup2+K2*(z2back-H2*xbup2);end  %----------------融合部分------------------------%两个局部滤波不相关条件下的简单全局融合p=inv(inv(p1)+inv(p2));%融合后的估计误差协方差xkfRWD(:,k)=p*(inv(p1)*xkf1RWD(:,k)+inv(p2)*xkf2RWD(:,k));%融合后的状态估计值
end%--------------------------误差计算--------------------------------
%初始化
messure_err_x1=zeros(1,N);
messure_err_x2=zeros(1,N);
kalman_err_x1=zeros(1,N);
RWD_err_x1=zeros(1,N);
kalman_err_x2=zeros(1,N);
RWD_err_x2=zeros(1,N);
for k=1:N%量测误差messure_err_x1(k)=abs(z1(k)-x(1,k));messure_err_x2(k)=abs(z2(k)-x(2,k));%Kalman估计偏差kalman_err_x1(k)=abs(xkf1(1,k)-x(1,k));kalman_err_x2(k)=abs(xkf2(2,k)-x(2,k));%RWD估计偏差RWD_err_x1(k)=abs(xkfRWD(1,k)-x(1,k));RWD_err_x2(k)=abs(xkfRWD(2,k)-x(2,k));
end%噪声图
figure;
subplot(2,2,1)
plot(w(1,:));xlabel('采样时间');ylabel('噪声');
title('第1状态值过程噪声');
subplot(2,2,2)
plot(w(2,:));xlabel('采样时间');ylabel('噪声');
title('第2状态值过程噪声');
subplot(2,2,3)
plot(v1);xlabel('采样时间');ylabel('噪声');
title('第1状态值第1传感器量测噪声');
subplot(2,2,4)
plot(v2);xlabel('采样时间');ylabel('噪声');
title('第2状态值第2传感器量测噪声');%局部滤波器1
figure;
t=2:N;
plot(t,x(1,t),'-k.',t,z1(t),'-b.',t,xkfRWD(1,t),'-r.',t,xkf1(1,t),'-g.');
legend('第1状态值','第1量测值','第1状态量RWD估计值','第1状态量Kalman估计值');
xlabel('采样时间');ylabel('位置');
title('局部滤波器1跟踪状态');%局部滤波器2
figure;
t=2:N;
plot(t,x(2,t),'-k.',t,z2(t),'-b.',t,xkfRWD(2,t),'-r.',t,xkf2(2,t),'-g.');
legend('第2状态值','第2量测值','第2状态量RWD估计值','第2状态量Kalman估计值');
xlabel('采样时间');ylabel('位置');
title('局部滤波器2跟踪状态');%局部滤波器1误差
figure;
hold on,box on;
plot(messure_err_x1,'-b.');
plot(kalman_err_x1,'-g.');
plot(RWD_err_x1,'-r.');
legend('量测','Kalman估计','RWD估计');
xlabel('采样时间');ylabel('误差');
title('局部滤波器1误差');%局部滤波器2误差
figure;
hold on,box on;
plot(messure_err_x2,'-b.');
plot(kalman_err_x2,'-g.');
plot(RWD_err_x2,'-r.');
legend('量测','Kalman估计','RWD估计');
xlabel('采样时间');ylabel('误差');
title('局部滤波器2误差');%量测值记录
figure;
hold on,box on;
plot(z1);
plot(z2);
xlabel('采样时间');ylabel('数值');
legend('量测1','量测2');
title('量测值记录');%检测记录
figure;
t=2:N;
subplot(2,1,1)
plot(t,S1(t),'-b.',t,Alarm(1,t),'-r.');
legend('攻击检测衡量值1','是否存在攻击1');
title('检测攻击1');
subplot(2,1,2)
plot(t,S2(t),'-b.',t,Alarm(2,t),'-r.');
legend('攻击检测衡量值2','是否存在攻击2');
title('检测攻击2');

效果及分析

隐匿攻击

分析

1、从攻击检测的角度说，在这种情况下，文献强调的是对攻击的检测，但并不是每个传感器的攻击发生的所有时刻都完美检出，而只是对存在攻击的传感器进行检出。
对于只要检出发生攻击的传感器这一要求，与文献中描述的结果一致：通过选择一个合适的阈值，可以获得极低的虚警率和漏警率。
2、其实从攻击检测原理的角度说，窗口长度取平均这种从统计的方式入手，对这种攻击叠加产生的（合并量测噪声）期望值的偏移进行检测，来对攻击进行检出的方式，检出时间一定是会有延迟的，而且由于随机性的存在，更不仅仅是延迟那么简单，而是不一定在何时检出，并不会很准确，因此窗口越长，检出率越高，检测效果越准确。
3、更进一步，从攻击检测原理的角度说，窗口长度取平均这种从统计的方式入手，对这种攻击叠加产生的（合并量测噪声）期望值的偏移进行检测，来对攻击进行检出的方式，就需要本身噪声和攻击都有较大波动，才能较好的体现出检测效果，因为大的波动会产生更大的期望值偏移，更容易检出，这也是论文中隐匿攻击部分采用的量测噪声和攻击标准差都为较大的1.1的原因。
4、从安全估计的误差的角度来说，依照文献仿真章节给出的效果图可以看出，实际上针对隐匿攻击的情况，RWD算法的估计误差与标准Kalman相差无几，而远远好于对比算法，这在我们的仿真中也进行了复现。

噪声设置

追踪效果

估计误差

可以看出与标准Kalman差不多

量测值记录

攻击检测

能够实现对发生攻击的传感器的检出

检测率

在客观的设置无攻击和有攻击的传感器量测噪声标准差都是1.1，窗口长度设为20的情况下进行200次循环实验，得到的检测率和虚警率，可以看出有91.5%的检测率，即8.5%漏警概率；同时有17%虚警率，由此可以证明算法有效。

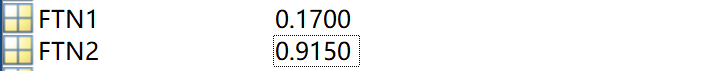
通过后期对窗口长度和阈值的优化，应该可以获得更高的检测率和更低的虚警率，这里不再推进。

非隐匿攻击

分析

这种情况下期望波动更大，更容易检测。

噪声设置

与前一致

追踪效果

估计误差

量测值记录

攻击检测

检测率

同样在客观的设置无攻击和有攻击的传感器量测噪声标准差都是1.1，窗口长度为20的情况下进行200次循环实验，得到的检测率和虚警率，可以看出有98%的检测率，即2%漏警概率；同时有5.5%虚警率，由此可以证明算法有效，且效果比极端隐匿更佳。

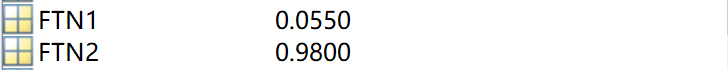
极端非隐匿攻击

分析

这种情况下可以通过适当的阈值选取和窗口长度，对攻击发生的对应时刻进行检出，但往往会有一定延迟，这取决于窗口的长度。另外这种检测效果也不是可以100%保证。
这种情况就能看出来文献中描述的：“一旦检测出攻击立马开始进行缓解攻击”。
也能体现出来：窗口长度的选取和阈值选取的折衷问题——窗口长度越长（同时阈值就要降），检测效果越好，非常直观的能体现出虚警率下降（包容了一些正常的噪声波动）；阈值选取高低也会直接在虚警率和漏警率上反映出来。
由于攻击与噪声相差较大，这里选取窗口长度为T，来获得更好的实时性。

噪声设置

追踪效果

估计误差

量测值记录

攻击检测

检测率

同样在客观的设置无攻击和有攻击的传感器量测噪声标准差都是0.1，窗口长度为10的情况下进行200次循环实验，得到的检测率和虚警率，可以看出有100%的检测率，即无漏警；同时也没有虚警，由此可以证明算法有效，且效果极佳。