基于Fisher判别的线性分类

线性分类器和Fisher判别

线性分类器

在机器学习领域，分类的目标是指将具有相似特征的对象聚集。而一个线性分类器则透过特征的线性组合来做出分类决定，以达到此种目的。对象的特征通常被描述为特征值，而在向量中则描述为特征向量。

Fisher判别

在模式识别中，费雪线性判别（Fisher’s linear discriminant）是一种线性判别方法，其意图是将d维空间中的数据点投影到c-1维空间上去，使得不同类的样本点在这个空间上的投影尽量分离，同类的尽量紧凑。

群内离散度与群间离散度

群内离散度要求的是距离越远越好，群间离散度的距离越近越好。
由上可知：“群内离散度”（样本类内离散矩阵）的计算公式为

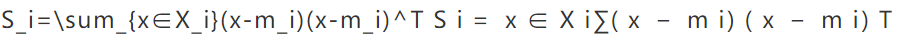
因为每一个样本有多维数据，因此需要将每一维数据代入公式计算后最后在求和即可得到样本类内离散矩阵。存在多个样本，重复该计算公式即可算出每一个样本的类内离散矩阵
“群间离散度”（总体类离散度矩阵）的计算公式为

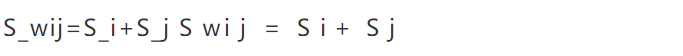
鸢尾花数据集被分成了三个样本，得到了三个总体类离散度矩阵，三个总体类离散度矩阵根据上述公式计算即可。

例题分析

• 题目
  
• 分析
  

Fisher判别python代码的推导

代码:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns#导入数据集
df = pd.read_csv('http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=0)
Iris1=df.values[0:50,0:4]
Iris2=df.values[50:100,0:4]
Iris3=df.values[100:150,0:4]#定义类均值向量
m1=np.mean(Iris1,axis=0)
m2=np.mean(Iris2,axis=0)
m3=np.mean(Iris3,axis=0)#定义类内离散度矩阵
s1=np.zeros((4,4))
s2=np.zeros((4,4))
s3=np.zeros((4,4))
for i in range(0,30,1):a=Iris1[i,:]-m1a=np.array([a])b=a.Ts1=s1+np.dot(b,a)
for i in range(0,30,1):c=Iris2[i,:]-m2c=np.array([c])d=c.Ts2=s2+np.dot(d,c)
for i in range(0,30,1):a=Iris3[i,:]-m3a=np.array([a])b=a.Ts3=s3+np.dot(b,a)#定义总类内离散矩阵