本文主要是介绍MNSGA-Ⅱ算法求解PMS（非关联并行机调度问题），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
本文为原创，如有转载借鉴，还请注明
目录
第一节 NSGA-Ⅱ算法简介
第二节 问题分析
2.1 问题描述
2.2 问题假设
2.3 变量说明
2.4 案例说明
第三节 算法设计
3.1 编码解码
3.2 初始化
3.3 交叉
3.4 变异
3.5 局部搜索
第四节 实验结果
4.1 实验设置
4.2 评价指标
4.3 结果分析
4.3.1 小中大单个算例分析
4.3.2 评价指标分析
4.3.3 综合分析
附录
第一节 NSGA-Ⅱ算法简介
NSGA-Ⅱ是最流行的多目标遗传算法之一，它降低了非劣排序遗传算法的复杂性，具有运行速度快，解集的收敛性好的优点，成为其他多目标优化算法性能的基准。
NSGA-Ⅱ算法是 Srinivas 和 Deb 于 2000 年在 NSGA 的基础上提出的，它比 NSGA算法更加优越：它采用了快速非支配排序算法，计算复杂度比 NSGA 大大的降低；采用了拥挤度和拥挤度比较算子，代替了需要指定的共享半径 shareQ，并在快速排序后的同级比较中作为胜出标准，使准 Pareto 域中的个体能扩展到整个 Pareto 域，并均匀分布，保持了种群的多样性；引入了精英策略，扩大了采样空间，防止最佳个体的丢失，提高了算法的运算速度和鲁棒性。
NSGA-Ⅱ就是在第一代非支配排序遗传算法的基础上改进而来，其改进主要是针对如上所述的三个方面：
①提出了快速非支配排序算法，一方面降低了计算的复杂度，另一方面它将父代种群跟子代种群进行合并，使得下一代的种群从双倍的空间中进行选取，从而保留了最为优秀的所有个体；
②引进精英策略，保证某些优良的种群个体在进化过程中不会被丢弃，从而提高了优化结果的精度；
③采用拥挤度和拥挤度比较算子，不但克服了NSGA中需要人为指定共享参数的缺陷，而且将其作为种群中个体间的比较标准，使得准Pareto域中的个体能均匀地扩展到整个Pareto域，保证了种群的多样性。
第二节 问题分析
2.1 问题描述
本文研究了一个非关联并行机节能调度问题，优化目标为最小化最大完工时间和总能耗。具体问题描述如下：有n个独立的订单JSN = {J1, J2, …, Jn}要在m个非关联并行机MSN = {M1, M2, …, Mm}上处理，每个订单均只有一道工序。已知订单i在机器j上的加工时间ti,j、订单i所分配加工机器上前一个加工订单为订单h时的准备时间pth,i、机器j的启停能耗SSj、机器j的单位时间加工能耗Ecptj及机器j的单位时间空载能耗NEcptj。对于每台机器上除第一个位置外加工的订单，如果当前机器启停能耗小于当前订单准备时的空载能耗，则选择采用机器开关机策略而不空载待机准备。该问题的关键在于如何安排各个订单的加工机器以及对应订单在加工机器上的加工位次从而实现最小化完工时间和总能耗的目标。
2.2 问题假设
为了便于进一步研究调度问题，我们在问题描述的基础上提出以下假设：
（1）每台机器在任何时刻只能处理一个订单；
（2）每个订单只能在一台机器上加工，且加工机器不允许被抢占；
（3）每台机器上第一个加工位置的订单无需准备即可开始加工；
（4）不考虑加工机器的故障或订单受外部因素影响而发生变化的情况。
2.3 变量说明
为了方便研究调度问题，我们对涉及到的关键变量进行了说明：
n：订单总数
m：机器总数
h, i：订单索引(i = 1, 2, …, n；h = 1, 2, …, n)
j：机器索引(j = 1, 2, …, m)
k：加工位置索引(k = 1, 2, …, n)
pth,i：订单i在订单h后加工的准备时间
ti,j：订单i在机器j上的加工时间
NEcptj：机器j上的单位时间空载能耗系数
Ecptj：机器j上的单位时间加工能耗系数
SSj：机器j的启停能耗
Cmax：加工所有订单的最大完工时间
E：加工完所有订单所需的总能耗
2.4 案例说明
为了更好地解释研究的问题，我们对一个并行机调度案例进行了分析，如图2-1所示。这个实例包括三台并行机器(M1, M2, M3)和十个订单(J1, J2, J3, J4, J5, J6, J7, J8, J9, J10)。每个订单只有一道工序。我们使用R来表示当前机器采用机器开关机策略。该策略的意思是，当机器启停能耗小于订单准备时的空载能耗时，选择采用机器开关机策略进行节能。该实例的关键在于如何安排各个订单在加工机器上的加工位次，以及对应订单在加工机器上的加工顺序，从而实现最小化完工时间和总能耗的目标。
图2-1(a)和(b)提供了解决该问题的同一种方案，区别在于图2-1(a)中的方案未采用机器开关机策略，而图2-1(b)中的方案则采用了该策略。图2-1(c)和(d)与图2-1(a)和(b)类似，区别在于图2-1(a)和(b)中的方案与图2-1(c)和(d)中的方案不同。
在图2-1(a)中，没有机器采用机器开关机策略进行重启。在图2-1(b)中，由于采用了该策略，机器M2和M3分别被重启了一次。在图2-1(c)中，没有机器采用机器开关机策略进行重启。在图2-1(d)中，由于采用了该策略，机器M2和M3分别被重启了两次。
显然，在相同的最大完工时间下，图2-1(b)在减少总能耗方面比图2-1(a)要好，图2-1(d)在减少总能耗方面也比图2-1(c)要好。引入机器开关机策略可以有效地降低总能耗。但是，随着该策略的引入，解决问题的复杂度也随之提高。
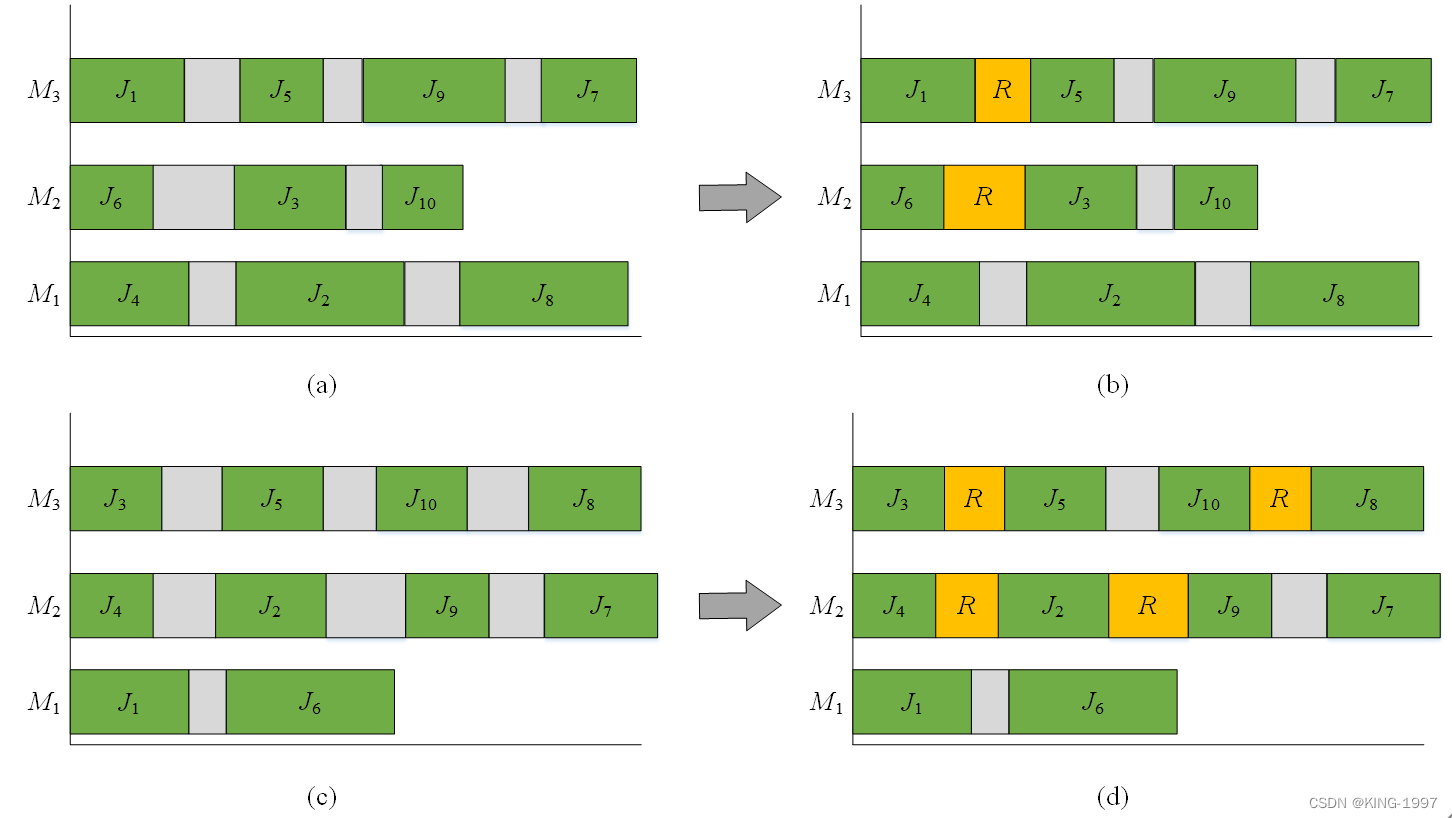
图2-1 并行机调度案例
第三节 算法设计
NSGA-Ⅱ算法框架的基础上，我们提出了MNSGA-Ⅱ元启发式算法来研究非关联并行机节能调度问题。
根据多目标非关联并行机节能调度问题的特征，我们主要在NSGA-Ⅱ算法框架的基础上做出了以下的改进：
（1）提出2个分别以最小化能源消耗和最小化最大完工时间为导向的初始化规则来生成高质量的初始调度方案；
（2）提出了1个快速均匀交叉算子来继承父代的基因，并快速完成交叉；
（3）设计了1个针对问题特征的局部搜索算子来加快算法的寻优速度且优化算法所求的最终调度方案。图3-1展示了MNSGA-Ⅱ算法的流程框架。
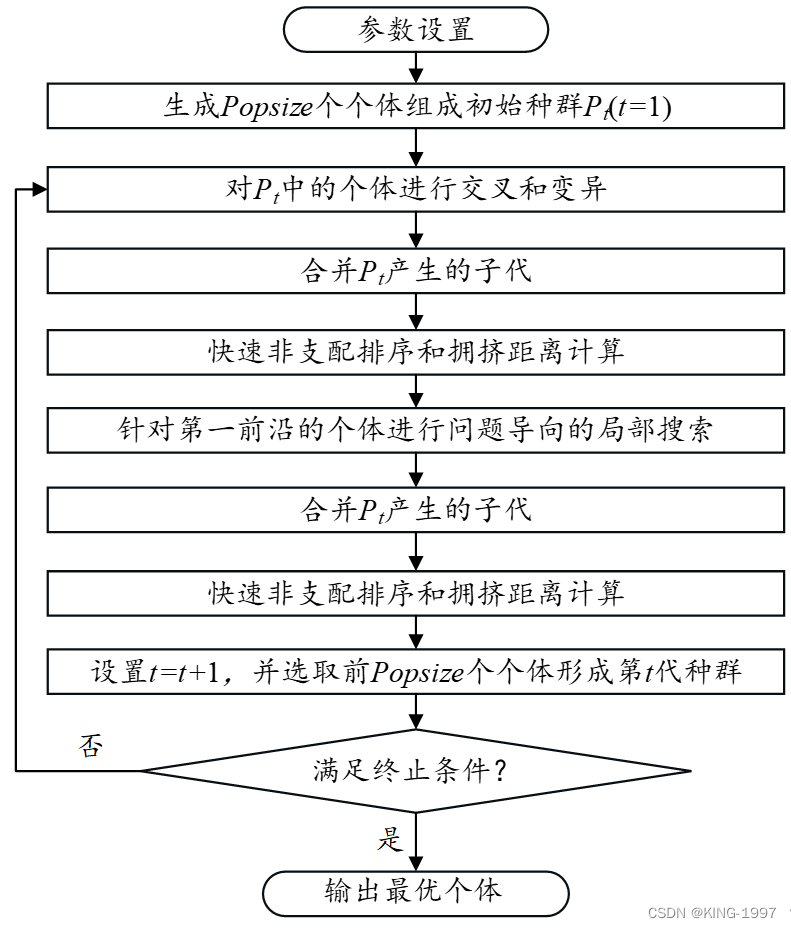
图3-1 MNSGA-Ⅱ算法的流程框架
3.1 编码解码
本课题研究的问题需要解决两个子问题：
（1）订单选择哪个机器进行加工；
（2）机器上每个订单按照什么顺序进行加工。
针对这些问题，我们设计了一个包括订单加工序列和机器加工序列的双层染色体来表示解决方案。染色体的第一层为订单加工序列OS(Order Sequence)可以表示为{OS1, OS2, …, OSi, OSi+1, …, OSn}，其中OSi∈{1, 2, …, n}，用于表示第i个加工的订单序号。染色体的第二层为机器加工序列MS(Machine Sequence){MS1, MS2, …, MSi, MSi+1, …, MSn}，其中MSi∈{1, 2, …, m}，用于表示订单OSi所分配的加工机器序号。对于分配给同一台机器的订单加工顺序，首先将这些订单在订单加工序列中的对应位置序号按照递增顺序排列，然后依据排序之后的列表中所在的位置即可确定这些订单在当前机器的加工顺序。
染色体编码解码示例如下：通过解码图3-2(a)中的染色体，可以得到图3-2(b)所示的加工信息。
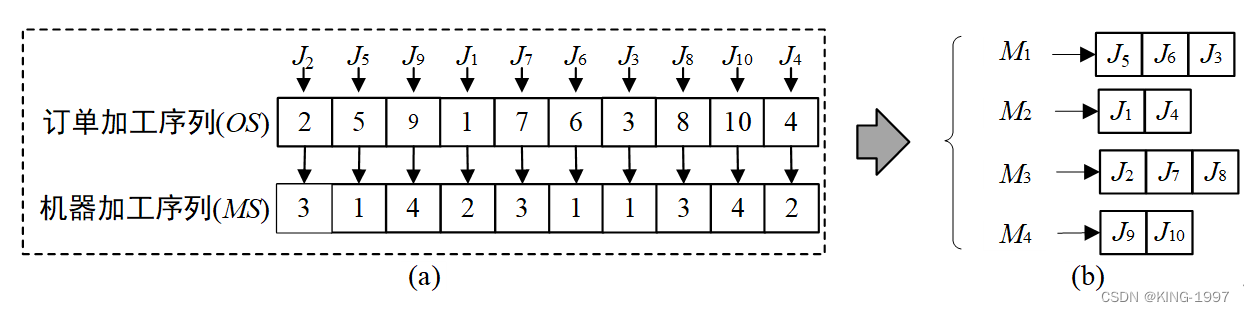
图3-2 染色体编码解码示例
3.2 初始化
高质量的初始解可以有效地加快算法在给定时间内的搜索速率，大大提升优化效果。本章节设计了2种分别侧重于最小化最大完工时间和最小化总能耗的初始化规则，以产生Popsize个高质量个体作为初始种群。
由于每个订单在各台机器上的加工时间、与加工序列相关的准备时间、每台机器的启停能耗、每台机器单位时间加工能耗系数、每台机器单位时间空载能耗系数都是预先知道的，因此若将每个订单分配给Cmaxi,j及Feci,j值相对较低的机器进行加工，可以有效地降低最大完工时间及总能耗。其中Cmaxi,j及Feci,j均为过程变量，Cmaxi,j表示将订单OSi分配给机器MSj时完成加工时的最大完工时间，Feci,j则表示将订单OSi分配给机器MSj时完成加工时所产生的总能耗。
3.3 交叉
在交叉阶段，我们引入均匀交叉算子(uniform crossover, UX)。在此基础上参照顺序交叉算子(Order Crossover, OX)对之进行优化，提出了OUX交叉算子。OUX交叉算子既继承了顺序交叉不会出现非法染色体的优点，又继承了均匀交叉保留原有父代基因的特点。因此，OUX交叉算子解决了均匀交叉可能出现非法染色体的问题，从而既能实现快速交叉，又能保留原有的基因信息，提高了算法的运算效率。我们采用OUX交叉算子操作染色体的OS层，采用UX交叉方式操作染色体的MS层。交叉的父代采用锦标赛选择法进行选择，交叉概率为Pc。为了便于操作，我们使用P1OS/P1MS和P2OS/P2MS分别表示OS/MS的两个父代，使用O1OS/O1MS和O2OS/O2MS分别表示OS/MS的两个子代。
两个交叉算子的主要步骤描述如下：
OUX交叉算子的描述：
步骤1：首先随机产生一个位于[0.2*Popsize, 0.5*Popsize]区间内的随机数Nc，然后随机选取Nc个位置（可以不连续）的基因构成子集Jset。
步骤2：从P1OS/P2OS上复制与Jset中订单相对应的基因，并将这些基因按照相同的顺序和位置复制到O1OS/O2OS上。
步骤3：将P1OS/P2OS上未曾在O2OS/O1OS上出现过的基因按照原始的顺序对应放置到O2OS/O1OS上的空闲位置。
UX交叉算子的描述：
步骤1：首先随机产生一个位于[0.2*Popsize, 0.5*Popsize]区间内的随机数Nc，然后随机选取Nc个位置（可以不连续）的基因构成子集Mset。
步骤2：从P1MS/P2MS上复制与Mset中订单相对应的基因，并将这些基因按照相同的顺序和位置复制到O1MS/O2MS上。
步骤3：将P1MS/P2MS当中剩余的基因按照原始的顺序和位置复制到O2MS/O1MS上。
关于染色体OS层采用的OUX交叉算子和MS层采用的UX交叉算子示例如图3-3所示。
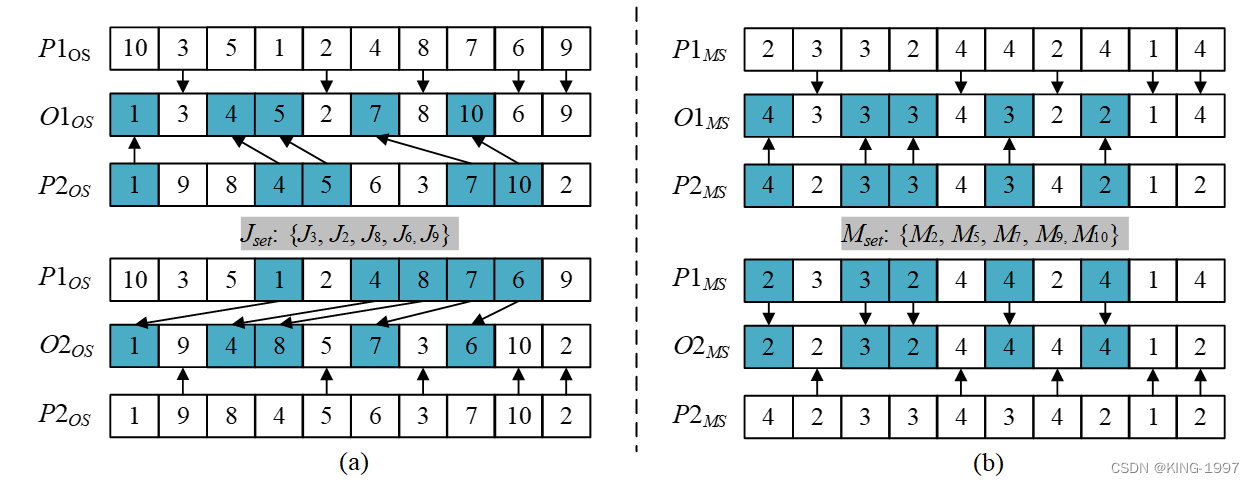
图3-3 染色体交叉示例
3.4 变异
为了使迭代过程中能够避免陷入局部最优，产生跳出局部最优的解，我们需要对每个父代染色体的OS/MS层使用随机交换算子交换其上两个位置的基因进行变异。变异的父代采用交叉后种群中的个体，变异概率为Pm。为了便于操作，我们使用POS/PMS分别表示OS/MS的父代，使用OOS/OMS分别表示OS/MS的子代。
关于染色体OS/MS层采用的随机交换变异算子示例如图3-4所示。
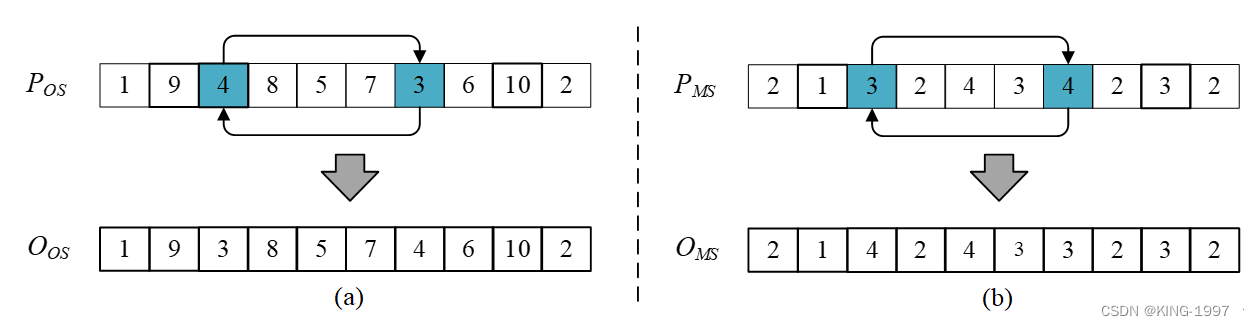
图3-4 染色体变异示例
3.5 局部搜索
为了加快整体算法的寻优速度，并且快速获得较优解。我们设计了1个以问题特征为导向的局部搜索算子，以最小化最大完工时间和总能耗。
针对每个个体所存储的信息（包含OS/MS双层染色体、最大完工时间、总能耗、调度序列、完工时间序列）进行分析，我们发现可以通过以下方法来优化调度方案可以得到更优方案：对于同一个加工方案，由于调度序列已知，可以通过选取最大完工时间所对应的机器上的订单，将之移至其他机器上进行加工处理。这样大概率可以降低最大完工时间，也可能降低能耗。
由于不是每次搜索都能得到支配原调度方案的新方案，我们设定了以下规则进行约束：
规则1：为了降低局部搜索的计算量，我们设定选择至多进行5次搜索；
规则2：为了避免陷入局部最优，我们设定每次搜索有25%的概率接受与原方案互不支配的解。即在5次搜索内，如果发现了支配原调度方案目标函数值的新方案，那就将新方案设置为新子代；否则，就对5次搜索后的新方案种群进行非支配排序、拥挤度计算、种群排序，以25%的概率接受选择新种群中序号为1的新方案作为新子代；
规则3：为了避免局部搜索耗费过长时间，我们设定只有第一前沿的个体参与局部搜索。如果第一前沿个体的数量大于Searchsize，则选择前Searchsize个个体进行局部搜索。
（算法的所有源码见文末）
第四节 实验结果
本章节通过一系列的实验验证了MNSGA-Ⅱ算法的有效性。我们首先介绍实验设置，包括测试算例、运行环境及性能指标。随后，分析算法的关键组成部分：2个初始化规则及1个局部搜索算子的性能表现。最后，给出MNSGA-Ⅱ算法与加了初始化规则不加局部搜索算子的NSGA-Ⅱ算法、不加初始化规则加局部搜索算子的NSGA-Ⅱ算法及原始的NSGA-Ⅱ算法的比较结果，综合评判MNSGA-Ⅱ算法的效果。
4.1 实验设置
由于目前针对并行机节能调度问题的相关研究比较少，因此，我们参考相关文献中的算例并以此为基准进行算例设计。算例参数n × m的组合是：{40, 80, 120, 160, 200}×{5, 10}。这些参数设置共形成10种组合。每种组合使用“n × m”标记。算例中其他参数设置如下：pth,i∈U[5, 15]，ti,j∈U[20, 50]，NEcptj∈U[5, 15]，Ecptj∈U[10, 20]，SSj∈U[50, 150]。为了保证实验的公平性及有效性，参考相关文献，设置测试算例运行时间为n × m秒。设置1/2的种群以能耗为引导进行初始化，1/4的种群以最大完工时间为引导进行初始化及1/4的种群随机初始初始化。
所有算法都是基于MATLAB R2022b编码，电脑运行配置：主频2.20GHz，内存16G，CPU 13th Gen Intel(R) Core(TM) i9-13900HX。
4.2 评价指标
本文采用IGD(inverted generational distance)，C(set coverage)及Rnd(the rate of non-dominated solutions)三个评价指标对算法产生的解进行评价。详细介绍如下：
（1）IGD：这是一个综合性评价指标，测量沿实际帕累托最优前沿的所有点到一组解集中距它们最接近的解的平均距离。集合F的IGD值的计算公式见公式(4-1)。
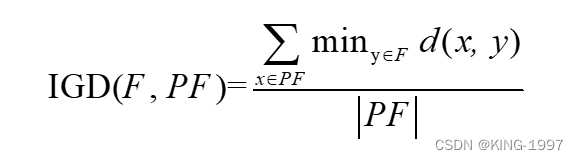
其中，d(x, y)表示点x和点y之间的欧几里德距离；PF表示真正的帕累托最优前沿。由于很难获得真正的帕累托最优前沿，所以本文将所有算法每次运行的帕累托前沿合并，然后对其进行非支配排序、拥挤度计算及种群排序。将最终获得的帕累托前沿作为参照最优前沿PF。IGD(F, PF)的值越小，表示F与PF之间的距离越小。IGD值越好，代表算法多样性和收敛性更好。为了避免数值差异化过大对IGD值造成影响，我们在计算IGD之前利用公式(4-2)对所有解的目标值进行归一化处理。其中，fimin和fimax分别是第i个优化目标的最小值和最大值。
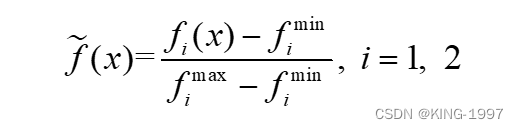
（2）C：C(A, B)表示集合B中的解至少被集合A中的一个解所支配的百分比。计算公式见公式(4-3)。
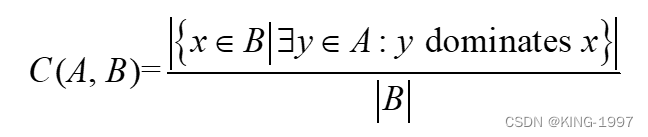
因此，C(A, B)的值越大，集合A的质量就越好。
（3）Rnd：算法求解的最优解中进入真正帕累托最优解集的数量占比。计算公式见公式(4-4)。
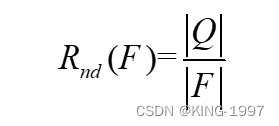
其中，Q={y∈F∣∀x∈PF, x不支配y}。因此，Rnd(F)的值越大，集合F的质量就越好。
4.3 结果分析
为了评估MNSGA-Ⅱ算法的表现，我们将其与加了初始化规则不加局部搜索算子的NSGA-Ⅱ算法、不加初始化规则加局部搜索算子的NSGA-Ⅱ算法及原始的NSGA-Ⅱ算法进行对比。
接下来将先分别针对小中大3个规模的单个算例分析MNSGA-Ⅱ算法关键成分的有效性，然后通过所有算例的IGD、C、Rnd评价指标对MNSGA-Ⅱ算法进行评价，最后综合分析评估MNSGA-Ⅱ算法的表现。
4.3.1 小中大单个算例分析
首先通过对40 × 10、120 × 10及200 × 10小中大不同规模的单个算例实验结果进行MNSGA-Ⅱ算法关键成分有效性分析：
（1）小算例：规模n × m为40 × 10，算例运行时间t为400秒。选取该组合下的1个测试算例的种群进行化对比图进行分析。四种算法种群进化对比图如图4-1及图4-2所示。
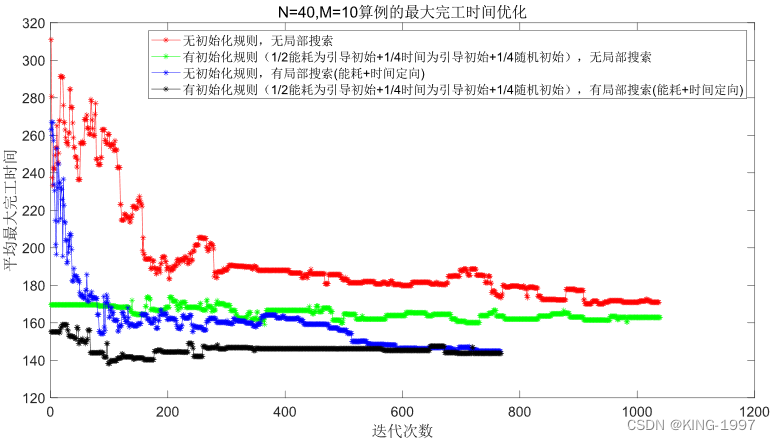
图4-1 40 × 10算例的最大完工时间种群进化对比图
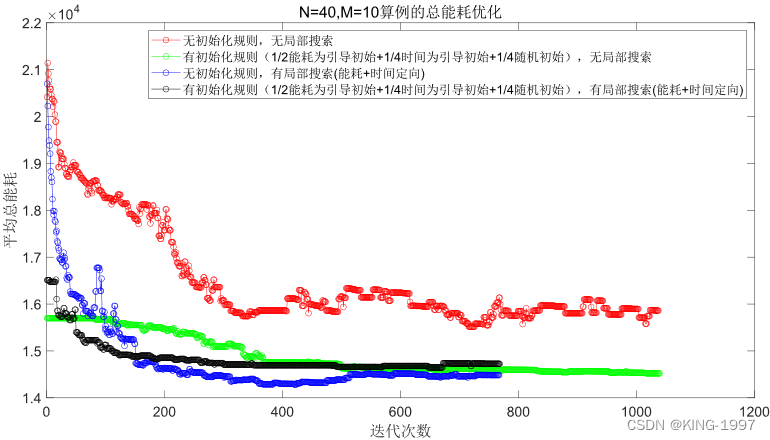
图4-2 40 × 10算例的总能耗种群进化对比图
通过对图4-1、图4-2的四种算法2个优化目标的种群进化对比图进行观察分析可以发现：针对小规模算例，所设计的初始化规则有较为直观的效果，可以将初始种群的优化目标最大完工时间及总能耗优化到一个较低的值。同时，局部搜索也有不错的效果，可以获得比原始NSGA-Ⅱ算法更好的最终解。
针对该规模的算例组合，通过将组合40 × 10下的5个算例结果进行非支配排序、拥挤度计算及种群排序后绘制四种算法的最优前沿对比图，从而避免个别情况的结果影响真实结果。四种算法最终所求得的最优前沿对比图如图4-3所示。
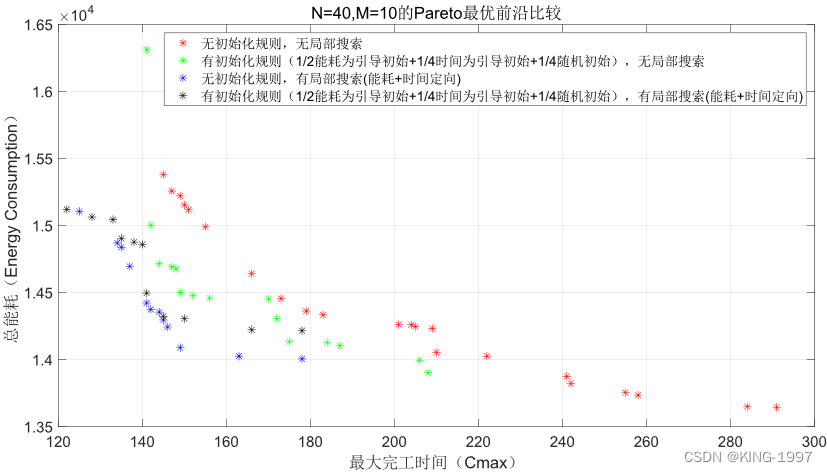图4-3 40 × 10算例的帕累托前沿对比图
通过对图4-3的四种算法最终所获得的帕累托前沿对比图进行观察分析可以发现：针对小规模算例，所设计的初始化规则、局部搜索均有一定的效果，可以获得比原始NSGA-Ⅱ算法更好的帕累托前沿，但是MNSGA-Ⅱ算法相对原始的NSGA-Ⅱ算法提升较小。
选取MNSGA-Ⅱ元启发式算法所求的一个最优生产调度方案绘制甘特图，如图4-4所示。
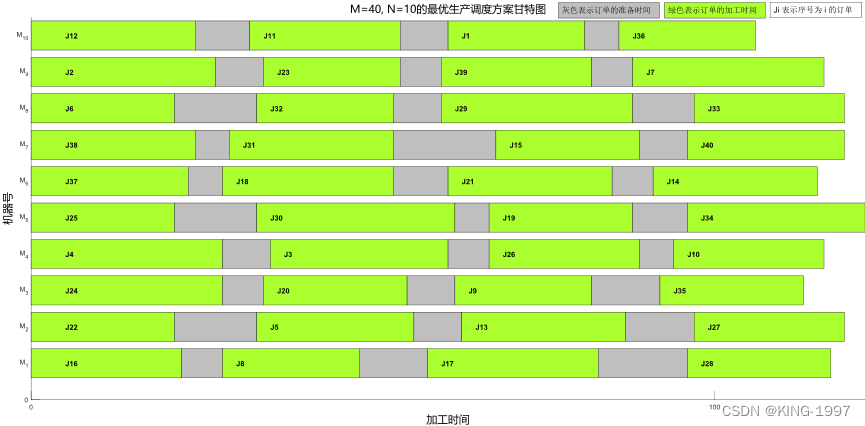
图4-4 40 × 10算例的最优生产调度方案甘特图
通过对图4-4的最优生产调度方案甘特图进行观察分析可以发现：最大完工时间所对应的机器为序号为5的机器。
（2）中算例：规模n × m为120 × 10，算例运行时间t为1200秒。选取该组合下的1个测试算例的种群进行化对比图进行分析。四种算法种群进化对比图如图4-5及图4-6所示。
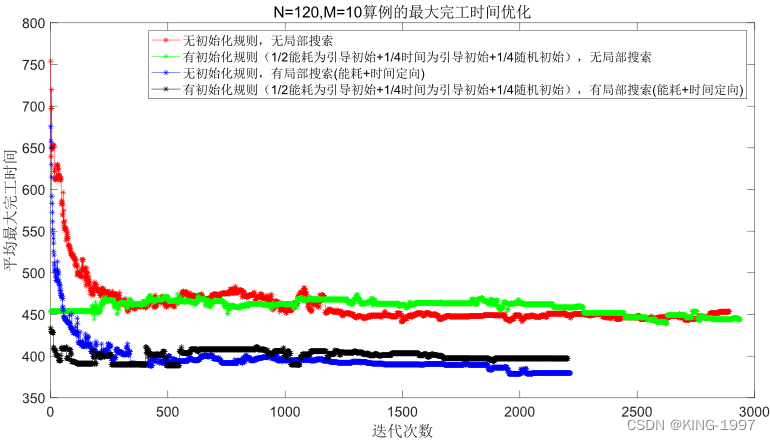
图4-5 120 × 10算例的最大完工时间种群进化对比图
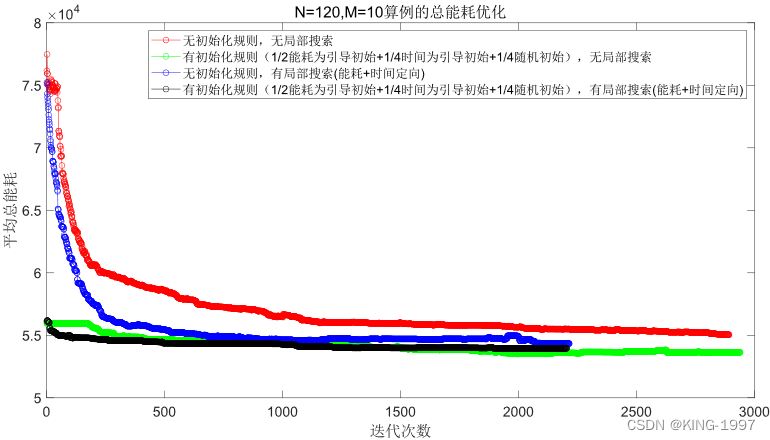
图4-6 120 × 10算例的总能耗种群进化对比图
通过对图4-5、图4-6的四种算法2个优化目标的种群进化对比图进行观察分析可以发现：针对中规模算例，所设计的初始化规则及局部搜索也有较为直观的优化效果。在将初始种群的优化目标最大完工时间及总能耗优化到一个较低的值的同时，还可以获得比原始NSGA-Ⅱ算法更好的最终解。
针对该规模的算例组合，通过将组合120 × 10下的5个算例结果进行非支配排序、拥挤度计算及种群排序后绘制四种算法的最优前沿对比图，从而避免个别情况的结果影响真实结果。四种算法最终所求得的最优前沿对比图如图4-7所示。
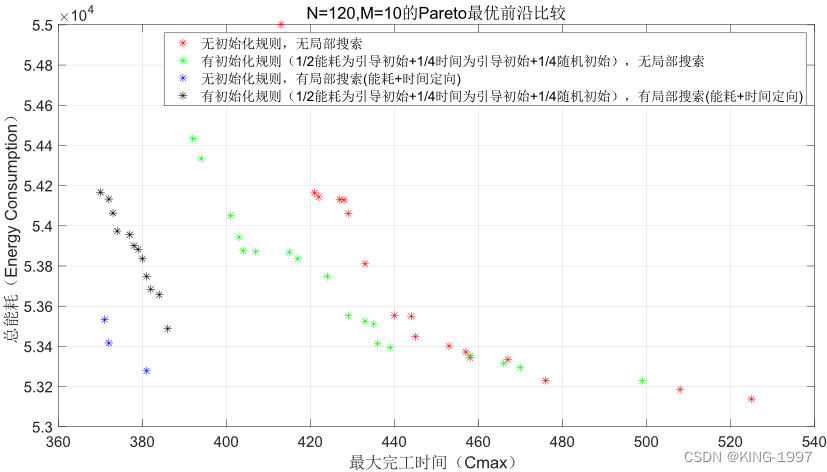
图4-7 120 × 10算例的帕累托前沿对比图
通过对图4-7的四种算法最终所获得的帕累托前沿对比图进行观察分析可以发现：针对中规模算例，所设计的初始化规则、局部搜索均有明显的效果，可以获得更好的帕累托前沿，且MNSGA-Ⅱ算法相对原始的NSGA-Ⅱ算法提升明显。
选取MNSGA-Ⅱ元启发式算法所求的一个最优生产调度方案绘制甘特图，如图4-8所示。
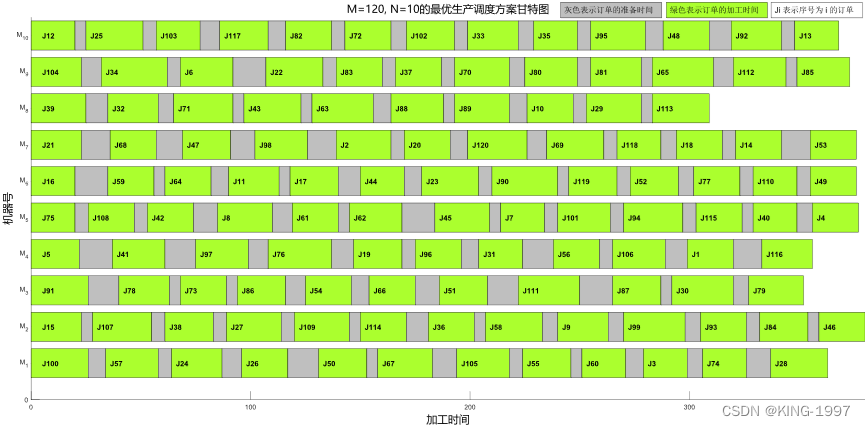
图4-8 120 × 10算例的最优生产调度方案甘特图
通过对图4-8的最优生产调度方案甘特图进行观察分析可以发现：最大完工时间所对应的机器为序号为2的机器。
（3）大算例：规模n × m为200 × 10，算例运行时间t为2000秒。选取该组合下的1个测试算例的种群进行化对比图进行分析。四种算法种群进化对比图如图4-9及图4-10所示。
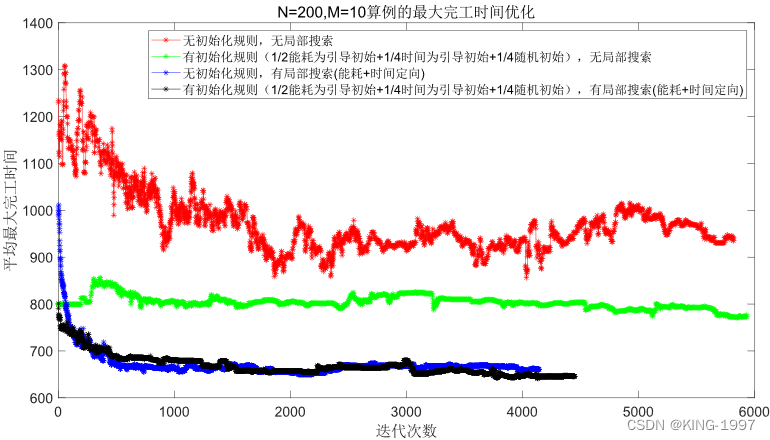
图4-9 200 × 10算例的最大完工时间种群进化对比图
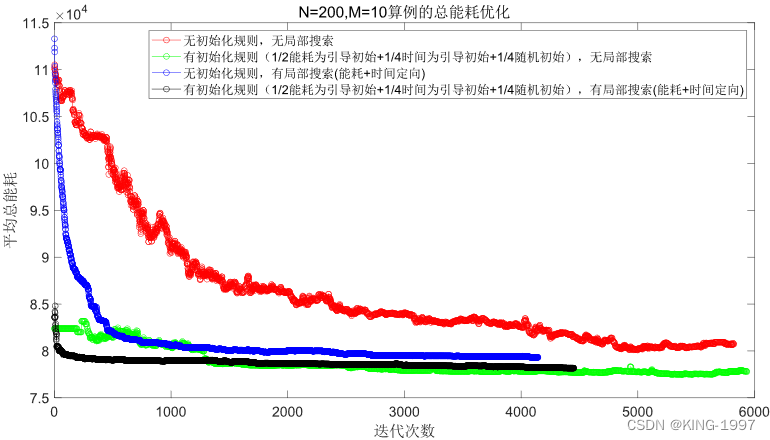
图4-10 200 × 10算例的总能耗种群进化对比图
通过对图4-9、图4-10的四种算法2个优化目标的种群进化对比图进行观察分析可以发现：针对大规模算例，所设计的初始化规则有直观的优化效果，既可以将初始种群的优化目标最大完工时间及总能耗快速优化到一个较低的值，又可以获得比原始NSGA-Ⅱ算法好得多的最终解。
针对该规模的算例组合，通过将组合200 × 10下的5个算例结果进行非支配排序、拥挤度计算及种群排序后绘制四种算法的最优前沿对比图，从而避免个别情况的结果影响真实结果。四种算法最终所求得的最优前沿对比图如图4-11所示。
图4-11 200 × 10算例的帕累托前沿对比图
通过对图4-11的四种算法最终所获得的帕累托前沿对比图进行观察分析可以发现：针对大规模算例，所设计的初始化规则、局部搜索均有较为明显的优化效果，可以将初始方案优化至一个较优的状态，可以获得更好的帕累托前沿，MNSGA-Ⅱ算法相对原始的NSGA-Ⅱ算法提升很大。
选取MNSGA-Ⅱ元启发式算法所求的一个最优生产调度方案绘制甘特图，如图4-12所示。
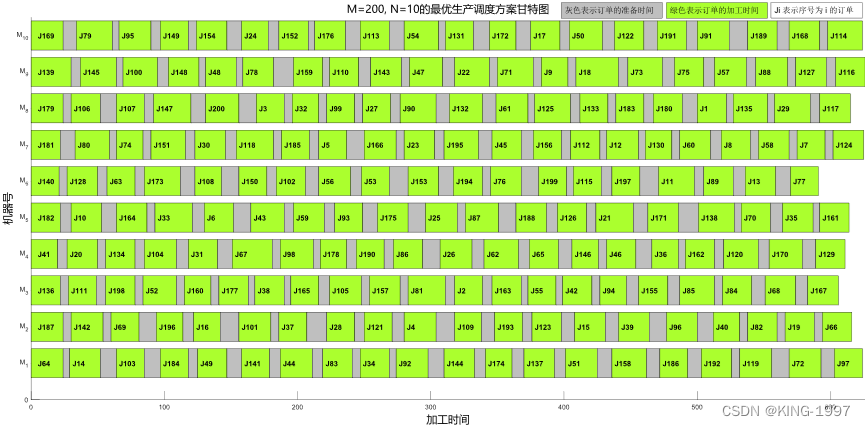
图4-12 200 × 10算例的最优生产调度方案甘特图
通过对图4-12的最优生产调度方案甘特图进行观察分析可以发现：最大完工时间所对应的机器为序号为9的机器。
4.3.2 评价指标分析
其次通过所有算例的IGD、C、Rnd评价指标对MNSGA-Ⅱ算法进行分析。所有算例测试的具体结果如表4-1、表4-2及表4-3所示。
表4-1 所有算法的IGD值
| n × m | MNSGA-Ⅱ | NO_Ini | NO_LS | NSGA-Ⅱ |
| 40×5 | 0.0031 | 0.0074 | 0.1197 | 0.1213 |
| 40×10 | 0.0748 | 0.0911 | 0.1363 | 0.1042 |
| 80×5 | 0.0431 | 0.0445 | 0.0770 | 0.1281 |
| 80×10 | 0.0513 | 0.0762 | 0.0551 | 0.0905 |
| 120×5 | 0.0939 | 0.1042 | 0.1101 | 0.1275 |
| 120×10 | 0.1137 | 0.1535 | 0.1768 | 0.2090 |
| 160×5 | 0.0605 | 0.1146 | 0.0836 | 0.1459 |
| 160×10 | 0.1379 | 0.2131 | 0.1736 | 0.3808 |
| 200×5 | 0.0714 | 0.1736 | 0.1593 | 0.2547 |
| 200×10 | 0.1336 | 0.1471 | 0.1568 | 0.3293 |
表4-2 所有算法的C值
| n × m | C(MNSGA-Ⅱ, NO_Ini) | C(MNSGA-Ⅱ, NO_LS) | C(MNSGA-Ⅱ, NSGA-Ⅱ) |
| 40×5 | 0.1538 | 0.7692 | 0.8235 |
| 40×10 | 0.1638 | 0.6667 | 0.6364 |
| 80×5 | 0.5000 | 0.5714 | 0.7500 |
| 80×10 | 0.5263 | 0.5278 | 0.8483 |
| 120×5 | 0.3254 | 0.4737 | 0.6296 |
| 120×10 | 0.2985 | 0.6667 | 0.7024 |
| 160×5 | 0.3782 | 0.7524 | 0.7737 |
| 160×10 | 0.6250 | 0.6500 | 1.0000 |
| 200×5 | 1.0000 | 0.3629 | 1.0000 |
| 200×10 | 0.4167 | 0.0556 | 0.7671 |
表4-3 所有算法的Rnd值
| n × m | MNSGA-Ⅱ | NO_Ini | NO_LS | NSGA-Ⅱ |
| 40×5 | 0.7500 | 0.8462 | 0.0000 | 0.0000 |
| 40×10 | 0.6727 | 1.0000 | 0.1333 | 0.2727 |
| 80×5 | 0.5714 | 0.4286 | 0.0714 | 0.0000 |
| 80×10 | 0.6843 | 0.4211 | 0.3556 | 0.2572 |
| 120×5 | 0.7621 | 1.0000 | 0.2105 | 0.1111 |
| 120×10 | 0.8033 | 1.0000 | 0.1356 | 0.1500 |
| 160×5 | 0.7053 | 1.0000 | 0.5862 | 0.0000 |
| 160×10 | 1.0000 | 0.2500 | 0.6800 | 0.0000 |
| 200×5 | 1.0000 | 0.3500 | 0.8571 | 0.0000 |
| 200×10 | 0.8286 | 0.5833 | 0.7444 | 0.0000 |
表4-1中的IGD值统计结果表明：对于近乎所有规模的算例，MNSGA-Ⅱ算法获得的IGD值基本都小于NO_Ini、NO_LS及NSGA-Ⅱ获得的IGD值。这表示MNSGA-Ⅱ算法求得的解更接近最优的帕累托最优前沿，且分布更均匀。
表4-2中的C值统计结果表明：对于近乎所有规模的算例，MNSGA-Ⅱ算法产生的解绝大部分不会被NO_Ini、NO_LS及NSGA-Ⅱ所支配。
表4-3中的Rnd值统计结果表明：MNSGA-Ⅱ算法所产生的解绝大部分都处于最优前沿，NO_Ini、NO_LS所产生的大部分解处于最优前沿，而NSGA-Ⅱ所产生的小部分解甚至无解处于帕累托最优前沿。
针对3个评价指标统计结果进行分析，可以发现所设计的MNSGA-Ⅱ算法比原始的NSGA-Ⅱ更优。
4.3.3 综合分析
将小中大单个算例的分析结果和IGD、C、Rnd评价指标的分析结果结合起来看，可以得出结论：所设计的MNSGA-Ⅱ算法相对原始的NSGA-Ⅱ有较大的提升，且所设计的2个初始化规则及1个局部搜索算子都可以明显优化算法得到的最终结果，帮助算法快速收敛获得较优的调度方案。对于不同规模的算例，MNSGA-Ⅱ算法的优化效果也不一样。对于小规模的算例，MNSGA-Ⅱ算法的优化效果较小。但是对于中大规模的算例，MNSGA-Ⅱ算法的优化效果较为显著，并且算法收敛的速度也快了很多。
综上所述，基于所有测试结果可以得出结论：相比原始NSGA-Ⅱ算法的表现，MNSGA-Ⅱ算法的性能表现更为优秀。
附录
注：灰色为代码解释，红色为代码命名
主程序（主循环）：main.m
%% 既包含种群初始化规则(1/2能耗为引导初始+1/4时间为引导初始+1/4随机初始)，也包含局部搜索（能耗+时间为导向），改进的NSGA-2算法
%% 清除变量并清屏
clear;
clc;
close all;
%% 设置参数
N=200;% 订单总数
M=10;% 机器总数
nPop=100;% 种群容量
MaxIter=9999;% 最大迭代次数
pCrossover=0.8;% 交叉率
pMutation=0.05;% 变异率
n1=nPop/4;%时间初始化个体数量
n2=nPop/2;%能耗初始化个体数量
n3=nPop/4;%随机初始化个体数量
%% 开始计时
t1=datevec(datetime);
%% 初始化种群
empty_individual.Position1=[];
empty_individual.Position2=[];
empty_individual.Cost=[];
empty_individual.Information.M_index=[];
empty_individual.Information.Finish_time=[];
empty_individual.Information.Cmax=[];
empty_individual.Information.Energy_consumption=[];
empty_individual.Rank=[];
empty_individual.DominationSet=[];
empty_individual.DominatedCount=[];
empty_individual.CrowdingDistance=[];
pop=repmat(empty_individual,nPop,1); % 复制
for i=1:nPoppop(i).Position1=randperm(N);if i<=n1pop(i).Position2=OrderAllocate1(pop(i).Position1,M,N);elseif n1<i&&i<=n1+n2pop(i).Position2=OrderAllocate2(pop(i).Position1,M,N);elsepop(i).Position2=randi(M,1,N);end[M_index,Finish_time,Cmax,Finall_energy_consumption]=Fitness(pop(i).Position1,pop(i).Position2,M,N);pop(i).Cost=[Cmax Finall_energy_consumption];pop(i).Information.M_index=M_index;pop(i).Information.Finish_time=Finish_time;pop(i).Information.Cmax=Cmax;pop(i).Information.Energy_consumption=Finall_energy_consumption;
end
%% 非支配排序
[pop,F]=NonDominatedSorting(pop);
%% 计算拥挤度
pop=CalcCrowdingDistance(pop,F);
%% 对个体排序
[pop,F]=SortPopulation(pop);
%% 主循环
for it4=1:MaxIterpopc=repmat(empty_individual,nPop/2,2);% 交叉for k=1:nPop/2if rand()<pCrossoverp1=TournamentSelect(pop);p2=TournamentSelect(pop);[popc(k,1).Position1,popc(k,2).Position1]=Crossover1(p1.Position1,p2.Position1);[popc(k,1).Position2,popc(k,2).Position2]=Crossover2(p1.Position2,p2.Position2);for i=1:2[M_index,Finish_time,Cmax,Finall_energy_consumption]=Fitness(popc(k,i).Position1,popc(k,i).Position2,M,N);popc(k,i).Cost=[Cmax Finall_energy_consumption];popc(k,i).Information.M_index=M_index;popc(k,i).Information.Finish_time=Finish_time;popc(k,i).Information.Cmax=Cmax;popc(k,i).Information.Energy_consumption=Finall_energy_consumption;endendendpopc=popc(:);popc=DeleteWhiteSpace(popc);% 变异nPopm=numel(popc);popm=repmat(empty_individual,nPopm,1);for k=1:nPopmp=popc(k);popm(k).Position1=Mutate(p.Position1,pMutation);popm(k).Position2=Mutate(p.Position2,pMutation);[M_index,Finish_time,Cmax,Finall_energy_consumption]=Fitness(popm(k).Position1,popm(k).Position2,M,N);popm(k).Cost=[Cmax Finall_energy_consumption];popm(k).Information.M_index=M_index;popm(k).Information.Finish_time=Finish_time;popm(k).Information.Cmax=Cmax;popm(k).Information.Energy_consumption=Finall_energy_consumption;end% 合并pop=[poppopcpopm];% 个体去重pop=DuplicateRemoval(pop);% 非支配排序[pop,F]=NonDominatedSorting(pop);% 计算拥挤度pop=CalcCrowdingDistance(pop,F);% 种群排序[pop,F]=SortPopulation(pop);% 防止溢出pop=pop(1:nPop);% 局部搜索Better_pop=LocalSearch(pop,numel(F{1}),M,N);% 合并pop=[popBetter_pop];% 个体去重pop=DuplicateRemoval(pop);% 非支配排序[pop,F]=NonDominatedSorting(pop);% 计算拥挤度pop=CalcCrowdingDistance(pop,F);% 种群排序[pop,F]=SortPopulation(pop);% 防止溢出pop=pop(1:nPop);% 记录评估值EvaluationValue=CalculatedEstimate(pop,numel(F{1}));D1(it4)=EvaluationValue(1);D2(it4)=EvaluationValue(2);D3(it4)=numel(F{1});% 存储 F1F1=pop(F{1});% 结果显示disp(['Iteration ' num2str(it4) ': Number of F1 Members = ' num2str(numel(F1))]);% 动态画图figure(1);PlotCosts(F1);pause(0.01);t2=datevec(datetime);t=etime(t2,t1);if t>M*Nbreak;end
end
%% 绘制迭代优化效果图
x=1:it4;
figure(2);
subplot(3,1,1);
plot(x,D1,'-*r');
xlabel('迭代次数');ylabel('平均最大完工时间');
subplot(3,1,2);
plot(x,D2,'-og');
xlabel('迭代次数');ylabel('平均总能耗');
subplot(3,1,3);
plot(x,D3,'-xb');
xlabel('迭代次数');ylabel('帕累托解集个数'); 初始化1（时间为引导）：OrderAllocate1.m
%% 订单启发式分配函数(时间为引导)
function Chro2=OrderAllocate1(Chro1,M,N)load Preparation_time.mat;%导入准备时间参数load Processing_time.mat;%导入加工时间参数load Noload_energy_consumption_coefficient.mat;%导入单位时间空载能耗系数load Energy_consumption_coefficient.mat;%导入单位时间加工能耗系数 Finish_time=zeros(M,N);%各机器加工完成时间M_index=zeros(M,N);%索引Tc=zeros(N,M);Selection_probability_temp1=zeros(N,M);Selection_probability_temp2=zeros(1,M);Selection_probability=zeros(N,M);sum=0;k=ones(1,M);for i=1:N%计算订单在每台机器上的完工时间for j=1:Mif k(j)==1Finish_time(j,k(j))=t(Chro1(i),j);Tc(Chro1(i),j)=Finish_time(j,k(j));elseFinish_time(j,k(j))=Finish_time(j,k(j)-1)+pt(Chro1(i),M_index(j,k(j)-1))+t(Chro1(i),j);Tc(Chro1(i),j)=Finish_time(j,k(j));endsum=sum+Tc(Chro1(i),j);end%计算订单选择每台机器的概率for l=1:MSelection_probability_temp1(Chro1(i),l)=Tc(Chro1(i),l)/sum;endSelection_probability_temp2=Selection_probability_temp1(Chro1(i),:);[Y,I]=sort(Selection_probability_temp2);for o=1:MSelection_probability(Chro1(i),o)=Y(M+1-find(I==o)); end%选择最大完工时间最小的机器Cmax_min=max(Selection_probability(Chro1(i),:));temp=Selection_probability(Chro1(i),:);Machinenumber=find(temp==Cmax_min);Machinenumber=Machinenumber(randi(length(Machinenumber)));%订单进行选择M_index(Machinenumber,k(Machinenumber))=Chro1(i);k(Machinenumber)=k(Machinenumber)+1;Chro2(i)=Machinenumber;%订单选择机器完成后进行多余参数重置for g=1:Mif g~=Chro2(i)Finish_time(g,k(g))=0;endendsum=0;end
end初始化2（能耗为引导）：OrderAllocate2.m
%% 订单启发式分配函数（能耗为引导）
function Chro2=OrderAllocate2(Chro1,M,N)load Preparation_time.mat;%导入准备时间参数load Processing_time.mat;%导入加工时间参数load Startstop_energy_consumption.mat;%导入机器启停能耗load Noload_energy_consumption_coefficient.mat;%导入单位时间空载能耗系数load Energy_consumption_coefficient.mat;%导入单位时间加工能耗系数Energy_consumption=zeros(M,N);%各机器加工能耗M_index=zeros(M,N);%索引Mc=zeros(N,M);Selection_probability_temp1=zeros(N,M);Selection_probability_temp2=zeros(1,M);Selection_probability=zeros(N,M);sum=0;k=ones(1,M);for i=1:N%计算订单在每台机器上的能耗for j=1:M for p=1:k(j)if p==1Energy_consumption(j,p)=Ecpt(j)*t(Chro1(i),j);Mc(Chro1(i),j)=Energy_consumption(j,k(j));elseif NEcpt(j)*pt(Chro1(i),M_index(j,p-1))>=Sec(j)Energy_consumption(j,p)=Energy_consumption(j,p-1)+Sec(j)+Ecpt(j)*t(Chro1(i),j);Mc(Chro1(i),j)=Energy_consumption(j,k(j));elseEnergy_consumption(j,p)=Energy_consumption(j,p-1)+NEcpt(j)*pt(Chro1(i),M_index(j,p-1))+Ecpt(j)*t(Chro1(i),j);Mc(Chro1(i),j)=Energy_consumption(j,k(j));endendendsum=sum+Mc(Chro1(i),j);end%计算订单选择每台机器的概率for l=1:MSelection_probability_temp1(Chro1(i),l)=Mc(Chro1(i),l)/sum;endSelection_probability_temp2=Selection_probability_temp1(Chro1(i),:);[Y,I]=sort(Selection_probability_temp2);for o=1:MSelection_probability(Chro1(i),o)=Y(M+1-find(I==o)); end%选择总能耗最小的机器Cmax_min=max(Selection_probability(Chro1(i),:));temp=Selection_probability(Chro1(i),:);Machinenumber=find(temp==Cmax_min);Machinenumber=Machinenumber(randi(length(Machinenumber)));%订单进行选择M_index(Machinenumber,k(Machinenumber))=Chro1(i);k(Machinenumber)=k(Machinenumber)+1;Chro2(i)=Machinenumber;%订单选择机器完成后进行多余参数重置for g=1:Mif g~=Chro2(i)Energy_consumption(g,k(g))=0;endendsum=0;end
end交叉（染色体1交叉）：Crossover1.m
%% 交叉操作
function [New_Chro1,New_Chro2]=Crossover1(Chro1,Chro2)L=length(Chro1);NC=randi([0.2*L,0.5*L],1,1);pos=randperm(L,NC);New_Chro1=zeros(1,L);New_Chro2=zeros(1,L);BZ_Chro1=Chro1;BZ_Chro2=Chro2;for i=1:NCNew_Chro1(pos(i))=Chro1(pos(i));New_Chro2(pos(i))=Chro2(pos(i));endfor i=1:Lfor j=1:NCif Chro2(i)==Chro1(pos(j))BZ_Chro2(i)=0;endif Chro1(i)==Chro2(pos(j))BZ_Chro1(i)=0;endendendcount1=1;count2=1;for i=1:Lfor j=count1:Lif New_Chro1(i)==0&&BZ_Chro2(j)~=0New_Chro1(i)=BZ_Chro2(j);count1=count1+1;break;endif New_Chro1(i)==0&&BZ_Chro2(j)==0count1=count1+1;endendendfor i=1:Lfor j=count2:Lif New_Chro2(i)==0&&BZ_Chro1(j)~=0New_Chro2(i)=BZ_Chro1(j);count2=count2+1;break;endif New_Chro2(i)==0&&BZ_Chro1(j)==0count2=count2+1;endendend
end交叉（染色体2交叉）：Crossover2.m
%% 交叉操作
function [New_Chro1,New_Chro2]=Crossover2(Chro1,Chro2)L=length(Chro1);NC=randi([0.2*L,0.5*L],1,1);New_Chro1=zeros(1,L);New_Chro2=zeros(1,L);pos=randperm(L,NC);pos_c=1:L;for i=1:NCNew_Chro1(pos(i))=Chro1(pos(i));New_Chro2(pos(i))=Chro2(pos(i));endfor i=1:Ls=find(pos==pos_c(i));if isempty(s)==1New_Chro1(pos_c(i))=Chro2(pos_c(i));New_Chro2(pos_c(i))=Chro1(pos_c(i));endend
end变异（染色体变异）：Mutate.m
%% 变异操作
function New_Chro=Mutate(Chro,pMutation)n=numel(Chro);pos=randperm(n,2);if rand()<pMutationtemp=Chro(pos(1));Chro(pos(1))=Chro(pos(2));Chro(pos(2))=temp;New_Chro=Chro;elseNew_Chro=Chro;end
end局部搜索（能耗+时间为引导）：LocalSearch.m
%% 局部搜索操作
function Better_pop=LocalSearch(pop,nF1,M,N)load Pc.mat;if nF1>20n=20;sui=randperm(nF1,n);elsen=nF1;sui=1:nF1;endempty_individual.Position1=[];empty_individual.Position2=[]; empty_individual.Cost=[];empty_individual.Information.M_index=[];empty_individual.Information.Finish_time=[];empty_individual.Information.Cmax=[];empty_individual.Information.Energy_consumption=[];empty_individual.Rank=[];empty_individual.DominationSet=[];empty_individual.DominatedCount=[];empty_individual.CrowdingDistance=[];Better_pop=repmat(empty_individual,n,1);New_pop=repmat(empty_individual,5,1);pos=zeros(2);for i=1:nfor j=1:5sign=sum(pop(sui(i)).Information.M_index~=0,2);sign=sign';[Machine_number,~]=find(pop(sui(i)).Information.Finish_time==pop(sui(i)).Cost(1));Machine_number=Machine_number(randi(length(Machine_number)));Possible_pop=repmat(empty_individual,sign(Machine_number),1);Optimal_energy_consumption=zeros(1,sign(Machine_number));for l=1:sign(Machine_number)Selection_set=1:M;pos(1,1)=Machine_number;pos(1,2)=l;Selection_set(pos(1,1))=[];pos(2,1)=Selection_set(randi(length(Selection_set)));if sign(pos(2,1))==0order1=pop(sui(i)).Information.M_index(pos(1,1),pos(1,2));order1_index=find(pop(sui(i)).Position1==order1);Possible_pop(l).Position1=pop(sui(i)).Position1;Possible_pop(l).Position2=[pop(sui(i)).Position2(1:order1_index-1) pos(2,1) pop(sui(i)).Position2(order1_index+1:end)];elsepos(2,2)=randi(sign(pos(2,1)));order1=pop(sui(i)).Information.M_index(pos(1,1),pos(1,2));order1_index=find(pop(sui(i)).Position1==order1);order2=pop(sui(i)).Information.M_index(pos(2,1),pos(2,2));order2_index=find(pop(sui(i)).Position1==order2); if order1_index<order2_indexPossible_pop(l).Position1=[pop(sui(i)).Position1(1:order1_index-1) pop(sui(i)).Position1(order1_index+1:order2_index-1) pop(sui(i)).Position1(order1_index) pop(sui(i)).Position1(order2_index:end)];Possible_pop(l).Position2=[pop(sui(i)).Position2(1:order1_index-1) pop(sui(i)).Position2(order1_index+1:order2_index-1) pos(2,1) pop(sui(i)).Position2(order2_index:end)];elsePossible_pop(l).Position1=[pop(sui(i)).Position1(1:order2_index-1) pop(sui(i)).Position1(order1_index) pop(sui(i)).Position1(order2_index:order1_index-1) pop(sui(i)).Position1(order1_index+1:end)];Possible_pop(l).Position2=[pop(sui(i)).Position2(1:order2_index-1) pos(2,1) pop(sui(i)).Position2(order2_index:order1_index-1) pop(sui(i)).Position2(order1_index+1:end)];endendOptimal_energy_consumption(l)=Pc(order1,pos(1,1))-Pc(order1,pos(2,1));endOptimal_energy_consumption_best=max(Optimal_energy_consumption);Index=find(Optimal_energy_consumption==Optimal_energy_consumption_best);Index=Index(randi(length(Index)));New_pop(j)=Possible_pop(Index);[M_index,Finish_time,Cmax,Finall_energy_consumption]=Fitness(New_pop(j).Position1,New_pop(j).Position2,M,N);New_pop(j).Cost=[Cmax Finall_energy_consumption];New_pop(j).Information.M_index=M_index;New_pop(j).Information.Finish_time=Finish_time;New_pop(j).Information.Cmax=Cmax;New_pop(j).Information.Energy_consumption=Finall_energy_consumption;p=New_pop(j);q=pop(sui(i));if Dominates(p,q)Better_pop(i)=New_pop(j);break;endif j==5temp=rand();if temp<0.25 [New_pop,F]=NonDominatedSorting(New_pop);New_pop=CalcCrowdingDistance(New_pop,F);[New_pop,F]=SortPopulation(New_pop);Better_pop(i)=New_pop(1);endend endendfor l=1:nif isempty(Better_pop(n-l+1).Cost)==1Better_pop(n-l+1)=[];endend
end适应度计算（求目标值最大完工时间及总能耗）：Fitness.m
%% 求适应度
function [M_index,Finish_time,Cmax,Finall_energy_consumption]=Fitness(Chro1,Chro2,M,N)load Preparation_time.mat;%导入准备时间参数load Processing_time.mat;%导入加工时间参数load Startstop_energy_consumption.mat;%导入机器启停能耗load Noload_energy_consumption_coefficient.mat;%导入单位时间空载能耗系数load Energy_consumption_coefficient.mat;%导入单位时间加工能耗系数Finish_time=zeros(M,N);%各机器加工完成时间Energy_consumption=zeros(M,N);%各机器加工能耗Finall_energy_consumption=0;%总能耗M_index=zeros(M,N);%索引k=ones(1,M);% 解码，获取机器加工信息for i=1:Nfor j=1:Mif Chro2(i)==jM_index(j,k(j))=Chro1(i);k(j)=k(j)+1;endendend% 求最大完工时间及总能耗% 求最大完工时间count=sum(M_index~=0,2);for j=1:M for k=1:count(j,1)if k==1Finish_time(j,k)=t(M_index(j,k),j);elseFinish_time(j,k)=Finish_time(j,k-1)+pt(M_index(j,k),M_index(j,k-1))+t(M_index(j,k),j);endendendCmax=max(max(Finish_time));% 求总能耗for j=1:M for k=1:count(j,1)if k==1Energy_consumption(j,k)=Ecpt(j)*t(M_index(j,k),j);elseif NEcpt(j)*pt(M_index(j,k),M_index(j,k-1))>=Sec(j)Energy_consumption(j,k)=Energy_consumption(j,k-1)+Sec(j)+Ecpt(j)*t(M_index(j,k),j);elseEnergy_consumption(j,k)=Energy_consumption(j,k-1)+NEcpt(j)*pt(M_index(j,k),M_index(j,k-1))+Ecpt(j)*t(M_index(j,k),j);endendendendM_Energy_consumption=max(Energy_consumption,[],2);for i=1:Mif i==1Finall_energy_consumption=M_Energy_consumption(i);elseFinall_energy_consumption=Finall_energy_consumption+M_Energy_consumption(i);endend
end竞标赛选择：TournamentSelect.m
%% 锦标赛选择
function p=TournamentSelect(pop)n=numel(pop);s=randperm(n,2);p1=pop(s(1));p2=pop(s(2));if p1.Rank<p2.Rankp=p1;elseif p1.Rank==p2.Rankif p1.CrowdingDistance>p2.CrowdingDistancep=p1;elsep=p2;endelsep=p2;end
end
去除空白个体：DeleteWhiteSpace.m
%% 个体去除空白
function New_pop=DeleteWhiteSpace(popc)n=numel(popc);for k=1:nif isempty(popc(n-k+1).Cost)==1popc(n-k+1)=[];continue;endendNew_pop=popc;
end
个体去重：DuplicateRemoval.m
%% 个体去重
function New_pop=DuplicateRemoval(pop)n=numel(pop);repeat=zeros(n,n);for i=2:nfor j=1:i-1if pop(i).Cost==pop(j).Costrepeat(i,j)=1;endendendbzw=sum(repeat~=0,2);for k=1:nif bzw(n-k+1)>0pop(n-k+1)=[];continue;endendNew_pop=pop;
end
非支配排序：NonDominatedSorting.m
%% 非支配排序
function [pop, F]=NonDominatedSorting(pop)nPop=numel(pop);for i=1:nPoppop(i).DominationSet=[];pop(i).DominatedCount=0;endF{1}=[];for i=1:nPopfor j=i+1:nPopp=pop(i);q=pop(j);if Dominates(p,q)p.DominationSet=[p.DominationSet j];q.DominatedCount=q.DominatedCount+1;endif Dominates(q.Cost,p.Cost)q.DominationSet=[q.DominationSet i];p.DominatedCount=p.DominatedCount+1;endpop(i)=p;pop(j)=q;endif pop(i).DominatedCount==0F{1}=[F{1} i];pop(i).Rank=1;endendk=1;while trueQ=[];for i=F{k}p=pop(i);for j=p.DominationSetq=pop(j);q.DominatedCount=q.DominatedCount-1;if q.DominatedCount==0Q=[Q j];q.Rank=k+1;endpop(j)=q;endendif isempty(Q)break;endF{k+1}=Q;k=k+1;end
end拥挤度计算：CalcCrowdingDistance.m
%% 计算拥挤度
function pop=CalcCrowdingDistance(pop,F)nF=numel(F);for k=1:nFCosts=[pop(F{k}).Cost];nobj=size(Costs,1);n=numel(F{k});d=zeros(n,nobj);for j=1:nobj[cj, so]=sort(Costs(j,:));d(so(1),j)=inf;for i=2:n-1d(so(i),j)=abs(cj(i+1)-cj(i-1))/abs(cj(1)-cj(end));endd(so(end),j)=inf;endfor i=1:npop(F{k}(i)).CrowdingDistance=sum(d(i,:));endend
end支配关系判别：Dominates.m
%% 判断支配关系
function z=Dominates(x,y)if isstruct(x)x=x.Cost;endif isstruct(y)y=y.Cost;endz=all(x<=y) && any(x<y);
end种群排序：SortPopulation.m
%% 种群排序
function [pop,F]=SortPopulation(pop)% 基于拥挤度排序[~,CDSO]=sort([pop.CrowdingDistance],'descend');pop=pop(CDSO);[~,RSO]=sort([pop.Rank]);pop=pop(RSO);Ranks=[pop.Rank];MaxRank=max(Ranks);F=cell(MaxRank,1);for r=1:MaxRankF{r}=find(Ranks==r);end
end评估值计算：CalculatedEstimate.m
%% 计算评估值
function EvaluationValue=CalculatedEstimate(pop,nF1)cost1=0;cost2=0;for k=1:nF1cost1=pop(k).Cost(1)+cost1;cost2=pop(k).Cost(2)+cost2;endEvaluationValue(1)=cost1/nF1;EvaluationValue(2)=cost2/nF1;
end绘图：PlotCosts.m
%% 绘制最终结果
function PlotCosts(pop)Costs=[pop.Cost];n=numel(Costs);x=zeros(1,n/2);y=zeros(1,n/2);for i=1:n/2x(i)=Costs(2*i-1);y(i)=Costs(2*i);endplot(x,y,'r*','MarkerSize',8);xlabel('最大完工时间（Cmax）');ylabel('总能耗（Energy_consumption）');title('Pareto解集');grid on;
end以下为参数生成，按需自取：
参数生成：ParameterGeneration.m
clear;
clc;
close all;
N=200;
M=10;
pt=round(5+(15-5)*rand(N,N));%相邻订单的准备时间（Preparation_time.mat）
t=round(20+(50-20)*rand(N,M));%订单i在机器j上的加工时间（Processing_time.mat）
Sec=round((50+(150-50)*rand(1,M)));%10台机器的启停能耗（Startstop_energy_consumption.mat）
NEcpt=round(5+(15-5)*rand(1,M));%10台机器的单位时间空载能耗系数（Noload_energy_consumption_coefficient.mat）
Ecpt=round(10+(20-10)*rand(1,M));%10台机器的单位时间加工能耗系数（Energy_consumption_coefficient.mat）
for i=1:Nfor j=1:Nif i==jpt(i,j)=0;endend
end参数处理再生成：ParameterGeneration1.m
clear;
clc;
load Processing_time.mat;%导入加工时间参数
load Energy_consumption_coefficient.mat;%导入单位时间加工能耗系数
N=200;
M=10;
Pc=zeros(N,M);
for i=1:Nfor j=1:MPc(i,j)=t(i,j)*Ecpt(j);end
end以下为甘特图绘制源码，按需自取：
主程序：main.m
clear;
clc;
close all;
load Final.mat;
FINAL_IGD=zeros(1,4);
FINAL_C=zeros(1,3);
FINAL_Rnd=zeros(1,4);
[PFF,F1,F2,F3,F4]=Normalization(PF,V1,V2,V3,V4);
for i=1:4if i==1FINAL_IGD(1,i)=IGD(F4,PFF);endif i==2FINAL_IGD(1,i)=IGD(F3,PFF);endif i==3FINAL_IGD(1,i)=IGD(F2,PFF);endif i==4FINAL_IGD(1,i)=IGD(F1,PFF);end
end
for i=1:3if i==1FINAL_C(1,i)=C(V4,V3);endif i==2FINAL_C(1,i)=C(V4,V2);endif i==3FINAL_C(1,i)=C(V4,V1);end
end
for i=1:4if i==1FINAL_Rnd(1,i)=Rnd(V4,PF);endif i==2FINAL_Rnd(1,i)=Rnd(V3,PF);endif i==3FINAL_Rnd(1,i)=Rnd(V2,PF);endif i==4FINAL_Rnd(1,i)=Rnd(V1,PF);end
endIGD值：IGD.m
%% PopObj：算法求得的pareto解集
%% PF：真实的解集
function Score = IGD(PopObj,PF)Distance = min(pdist2(PF,PopObj),[],2);Score = mean(Distance);
endC值：C.m
%% 求解C值
function Score = C(A,B)n1=numel(A);n2=numel(B);DominatedCount=0;for i=1:n2for j=1:n1if Dominates(A(j),B(i))DominatedCount=DominatedCount+1;break;endendendScore=DominatedCount/n2;
endRnd值：Rnd.m
%% 求解Rnd值
function Score = Rnd(F,PF)n1=numel(F);n2=numel(PF);InCount=0;for i=1:n1for j=1:n2if F(i).Cost==PF(j).CostInCount=InCount+1;endendendScore=InCount/n1;
end数据处理：Process.m
%% 处理数据
function F=Process(pop)Costs=[pop.Cost];n=numel(Costs);x=zeros(1,n/2);y=zeros(1,n/2);for i=1:n/2F(i,1)=Costs(2*i-1);F(i,2)=Costs(2*i);end
end数据归一化：Normalization.m
%% 数据归一化
function [PFF,F1,F2,F3,F4]=Normalization(PF,V1,V2,V3,V4)P1=Process(V1);P2=Process(V2);P3=Process(V3);P4=Process(V4);F=Process(PF);FA=[P1P2P3P4F];n(1)=numel(P1(:,1));n(2)=numel(P2(:,1));n(3)=numel(P3(:,1));n(4)=numel(P4(:,1));n(5)=numel(F(:,1));FA=FA';FA=mapminmax(FA,0,1);FA=FA';count=1;for i=1:5if i==1F1=FA(count:n(1),:);endif i==2F2=FA(count:n(1)+n(2),:);endif i==3F3=FA(count:n(1)+n(2)+n(3),:);endif i==4F4=FA(count:n(1)+n(2)+n(3)+n(4),:);endif i==5PFF=FA(count:n(1)+n(2)+n(3)+n(4)+n(5),:);endcount=count+n(i);end
end支配关系判别：Dominates.m
%% 判断支配关系
function z=Dominates(x,y)if isstruct(x)x=x.Cost;endif isstruct(y)y=y.Cost;endz=all(x<=y) && any(x<y);
end这篇关于MNSGA-Ⅱ算法求解PMS（非关联并行机调度问题）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
