【FinE】Portfolio Optimization Examples

投资组合案例

• how to set up mean-variance portfolio optimization problems thatr focus on the two-fund theorem（两基金分离定理）
• the impact of transaction costs and turnover constraints
• how to obtain portfolios that maximize the Sharpe Ratio
• how to set up two popular hedge fund strategies : dollar-neutral and 130-30 portfolios.

数据预处理

%% 读入数据
load BlueChipStockMoments
mret=MarketMean;
mrsk=sqrt(MarketVar);
cret=CashMean;
crsk=sqrt(CashVar);

建立Portfolio Object

%% 建立portfolio object
p=Portfolio('AssetList', AssetList, 'RiskFreeRate', CashMean);
p=setAssetMoments(p, AssetMean, AssetCovar);% 等权重作为初始权重
p=setInitPort(p, 1/p.NumAssets);
[ersk, eret]=estimatePortMoments(p, p.InitPort);
% plot
clf;
portfolioexamples_plot('Asset Risks and Returns', ...{'scatter', mrsk, mret, {'Market'}}, ...{'scatter', crsk, cret, {'Cash'}}, ...{'scatter', ersk, eret, {'Equal'}}, ...{'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

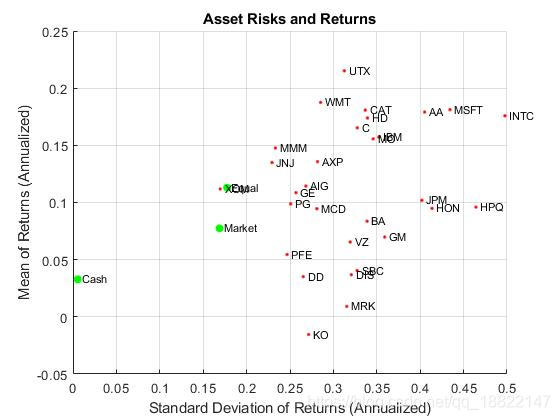
建立投资组合优化问题

计算有效前沿和相应的矩信息

%% portfolio optimization problem
p=setDefaultConstraints(p);
pwgt=estimateFrontier(p, 20);
[prsk, pret]=estimatePortMoments(p, pwgt);% plot efficient
clf;
portfolioexamples_plot('Efficient Frontier', ...{'line', prsk, pret}, ...{'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ...{'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

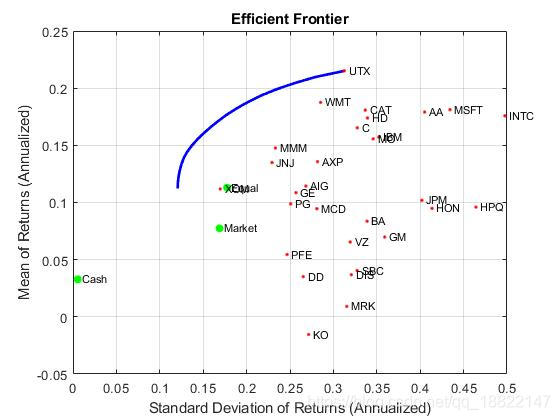
有限前沿上的切线

%% Tangent Line to the Efficient Frontier
q=setBudget(p, 0, 1);
qwgt=estimateFrontier(q, 20);
[qrsk, qret]=estimatePortMoments(q, qwgt);% Plot efficient frontier with tangent line
portfolioexamples_plot('Efficient Frontier with Tangent Line', ...{'line', prsk, pret}, ...{'line', qrsk, qret, [], [], 1}, ...{'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ...{'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

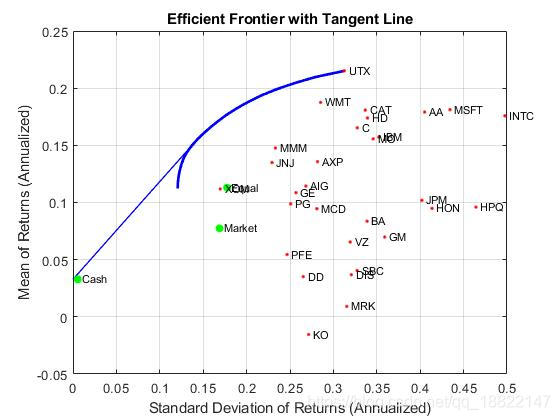
风险和收益率的范围

获得在有效前沿上组合的风险和收益的范围，使用estimateFrontierLimits

%% Obtain Range of Risks and Returns
[rsk, ret]=estimatePortMoments(p, estimateFrontierLimits(p));
display(rsk);
display(ret);

找到给定目标收益和目标风险的投资组合

%% Find a portfolio with a targeted return and targeted risk
t_return = 0.20; % 年化收益目标
t_risk = 0.15; % 年化风险目标awgt=estimateFrontierByReturn(p, t_return/12);
[arsk, aret]=estimatePortMoments(p, awgt);bwgt=estimateFrontierByRisk(p, t_risk/12);
[brsk, bret]=estimatePortMoments(p, bwgt);% plot
portfolioexamples_plot('Efficient Frontier with Targeted Portfolios', ...{'line', prsk, pret}, ...{'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ...{'scatter', arsk, aret, {sprintf('%g%% Return',100*t_return)}}, ...{'scatter', brsk, bret, {sprintf('%g%% Risk',100*t_risk)}}, ...{'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

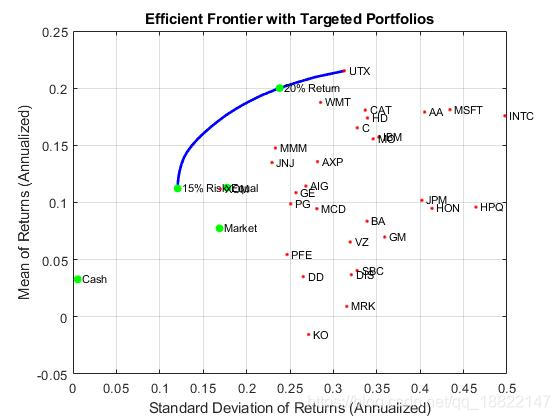
使用dataset对象查看成分资产

%% 查看组合成分资产
aBlotter=dataset({100*awgt(awgt>0), 'Weight'}, 'obsnames', p.AssetList(awgt>0));
displayPortfolio(sprintf('Portfolio with %g%% Target Return', 100*t_return), aBlotter, false);

bBlotter=dataset({100*bwgt(bwgt>0), 'Weight'}, 'obsnames', p.AssetList(bwgt>0));
displayPortfolio(sprintf('Portfolio with %g%% Target Return', 100*t_risk), bBlotter, false);

交易费用(Transaction Costs)

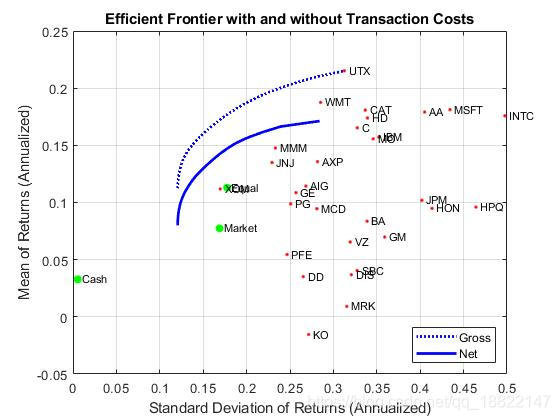
考虑交易费用transcation costs的组合优化问题，对比总收益gross和净收益net

%% Transaction Costs
BuyCost=0.0020;
SellCost=0.0020;
q=setCosts(p, BuyCost, SellCost);
qwgt=estimateFrontier(q, 20);
[qrsk, qret]=estimatePortMoments(q, qwgt);portfolioexamples_plot('Efficient Frontier with and without Transaction Costs', ...{'line', prsk, pret, {'Gross'}, ':b'}, ...{'line', qrsk, qret, {'Net'}}, ...{'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ...{'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

交易量约束(Turnover Constraint)

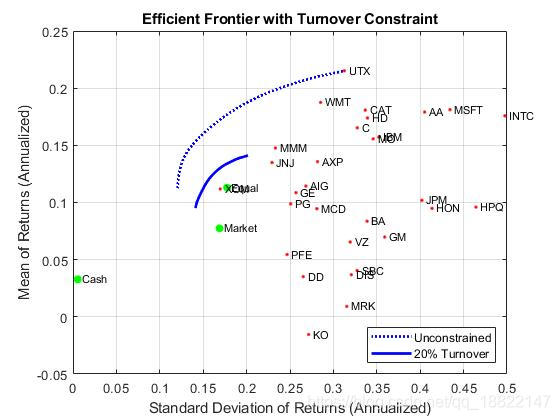
The following example demonstrates that a turnover constraint produces an efficient frontier in neighborhood of an initial portfolio that may restrict trading. Moreover, the introduction of a turnover constraint often implies that multiple trades may be necessary to shift from an initial portfolio to an unconstrainted efficient frontier. Consequently, the turnover constraint introduces a form of time diversification that can spread trades out over multiple time periods. In this example, note that the sum of purchases and sales from the estimateFrontier function confirms that the turnover constraint has been satisfied.

%% Turnover Constraint
BuyCost=0.0020;
SellCost=0.0020;
Turnover=0.2;q=setCosts(p, BuyCost, SellCost);
q=setTurnover(q, Turnover);[qwgt, qbuy, qsell]=estimateFrontier(q, 20);
[qrsk, qret]=estimatePortMoments(q, qwgt);portfolioexamples_plot('Efficient Frontier with Turnover Constraint', ...{'line', prsk, pret, {'Unconstrained'}, ':b'}, ...{'line', qrsk, qret, {sprintf('%g%% Turnover', 100*Turnover)}}, ...{'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ...{'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

追踪误差约束(Tracking-Error Constraint)

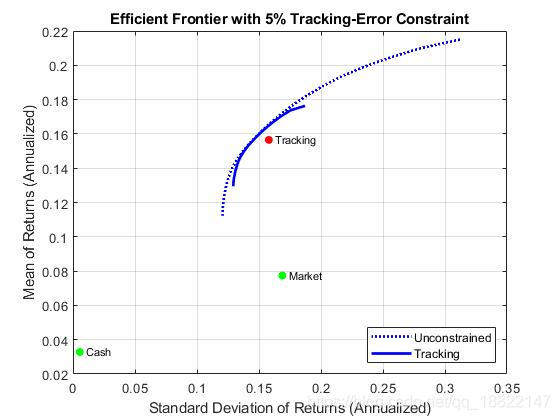
The Portfolio object can handle tracking-error constraints, where tracking-error is relative risk of portfolio compared with a tracking portfolio. In this example, a sub-collection of nine assets forms an equally-weighted tracking portfolio. The goal is to find efficient portfolios with tracking errors that are within 5% of this tracking portfolio.

%% tracking-error constraint
ind=[15, 16, 20, 21, 23, 25, 27, 29, 30];
TrackingError=0.05/sqrt(12);
TrackingPort=zeros(30, 1);
TrackingPort(ind)=1;
TrackingPort=(1/sum(TrackingPort))*TrackingPort; % 初始为等权重q=setTrackingError(p, TrackingError, TrackingPort);
qwgt=estimateFrontier(q, 20);
[qrsk, qret]=estimatePortMoments(q, qwgt);
[trsk, tret]=estimatePortMoments(q, TrackingPort);portfolioexamples_plot('Efficient Frontier with 5% Tracking-Error Constraint', ...{'line', prsk, pret, {'Unconstrained'}, ':b'}, ...{'line', qrsk, qret, {'Tracking'}}, ...{'scatter', [mrsk, crsk], [mret, cret], {'Market', 'Cash'}}, ...{'scatter', trsk, tret, {'Tracking'}, 'r'});

结合交易量约束和追踪误差约束

交易量约束为最大30%的资产可以被交易，最大允许5%的追踪误差.

Note that the turnover to get from the initial portfolio to the tracking portfolio is 70% so that an upper bound of 30% turnover means that the efficient frontier will lie somewhere between the initial portfolio and the tracking portfolio.

%% combined turnover and tracking error constraints
Turnover=0.3;
InitPort=(1/q.NumAssets)*ones(q.NumAssets, 1); %初始投组合
ind = [15, 16, 20, 21, 23, 25, 27, 29, 30]; % 包含在tracking portfolio中的资产编号TrackingError=0.05/sqrt(12);
TrackingPort=zeros(30, 1);
TrackingPort(ind)=1;
TrackingPort=(1/sum(TrackingPort))*TrackingPort;q=setTurnover(q, Turnover, InitPort); % 设置追踪误差约束
qwgt=estimateFrontier(q, 20);[qrsk, qret]=estimatePortMoments(q, qwgt); % 双约束条件下有效前沿组合矩信息
[trsk, tret]=estimatePortMoments(q, TrackingPort); 
[ersk, eret]=estimatePortMoments(q, InitPort);% plot
portfolioexamples_plot('Efficient Frontier with Turnover and Tracking-Error Constraint', ...{'line', prsk, pret, {'Unconstrained'}, ':b'}, ...{'line', qrsk, qret, {'Turnover & Tracking'}}, ...{'scatter', [mrsk, crsk], [mret, cret], {'Market', 'Cash'}}, ...{'scatter', trsk, tret, {'Tracking'}, 'r'}, ...{'scatter', ersk, eret, {'Initial'}, 'b'});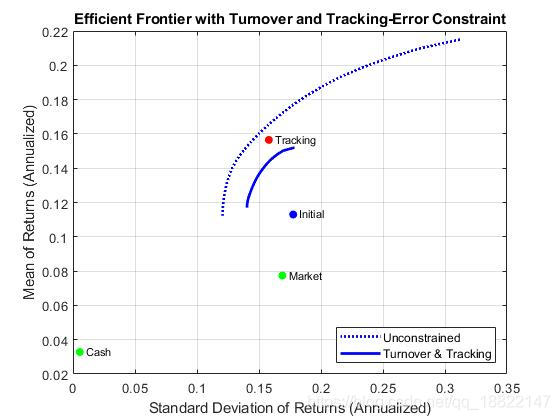

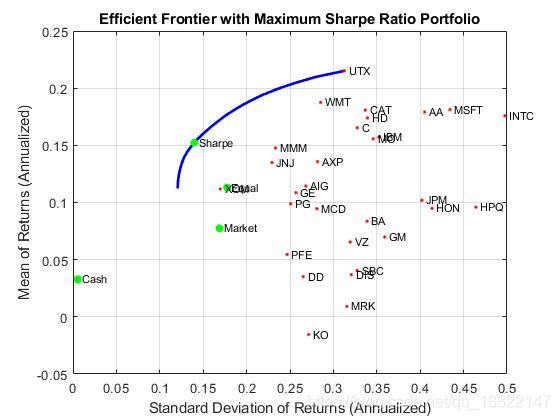
最大化Sharpe Ratio

The Sharpe ratio is a measure of return-to-risk that plays an import role in portfolio anaysis. Specifically, a portfolio that maximizes the Sharpe ratio is also the tangency portfolio on the efficient frontier from the mutual fund theorem. The maximum Sharpe ratio portfolio is located on the efficient frontier with the function estimateMaxSharpeRatio and the dataset¹

%% Maximize the Sharpe Ratio
p=setInitPort(p, 0);
swgt=estimateMaxSharpeRatio(p);
[srsk, sret]=estimatePortMoments(p, swgt);% plot
portfolioexamples_plot('Efficient Frontier with Maximum Sharpe Ratio Portfolio', ...{'line', prsk, pret}, ...{'scatter', srsk, sret, {'Sharpe'}}, ...{'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ...{'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

显示最大Sharpe ratio组合的成分资产

% display portfolio assets
Blotter=dataset({100*swgt(swgt>0), 'Weight'}, 'obsnames', AssetList(swgt>0));
displayPortfolio('Portfolio with Maximum Sharpe Ratio', Blotter, false);

图像显示最大Sharpe Ratio Point

%% confirm that maximum sharpe ratio is a maximum
psratio=(pret-p.RiskFreeRate) ./ prsk;
ssratio=(sret-p.RiskFreeRate) / srsk;subplot(2, 1, 1);
hold on;
plot(prsk, pret, '--', 'LineWidth', 1); % 有效前沿(均值-方差)
scatter(srsk, sret, 'r', 'filled');
hold off;
title('\bfEfficient Frontier');
xlabel('Portfolio Risk');
ylabel('Portfolio Return');subplot(2,1,2);
plot(prsk, psratio, '--', 'LineWidth', 1); % 有效前沿(SR-方差)
hold on;
scatter(srsk, ssratio, 'r', 'filled');
title('\bfSharpe Ratio');
xlabel('Portfolio Risk');
ylabel('Sharpe Ratio');
hold off;

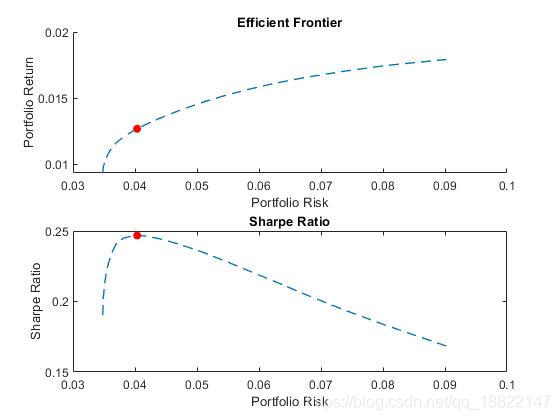
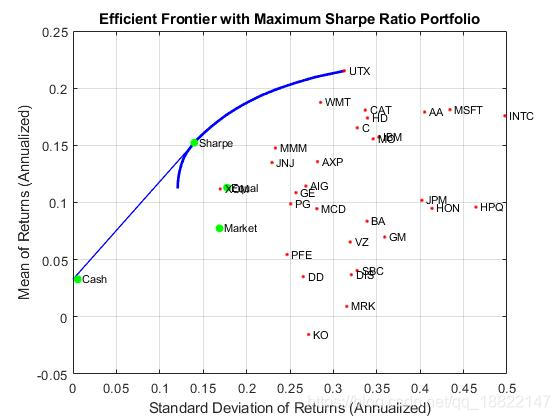
Sharpe Point组合为切点组合

the plot demonstrates that the portfolio that maximizes the Sharpe ratio is also a tangency porfolio.

%% illustrate that sharpe is the tangent portfolio
q=setBudget(p, 0, 1);
qwgt=estimateFrontier(q, 20);
[qrsk, qret]=estimatePortMoments(q, qwgt);% plot
portfolioexamples_plot('Efficient Frontier with Maximum Sharpe Ratio Portfolio', ...{'line', prsk, pret}, ...{'line', qrsk, qret, [], [], 1}, ...{'scatter', srsk, sret, {'Sharpe'}}, ...{'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ...{'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

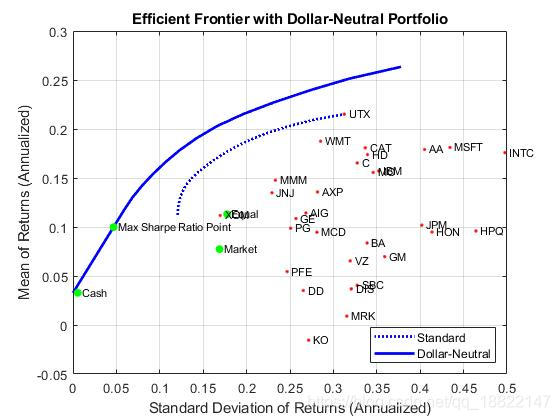
Dollar-Neutral Hedge-Fund Structure

组合优化方法在对冲基金管理管理中的应用，两种常用的策略为货币中性策略(dollar-neutral)和(130-30)策略.

• dollar neutral策略：对空头头寸和多头头寸均衡投资，使得组合总仓位为0

To set up a dollar-neutral portfolio, start with the standard portfolio problem and set the maximum exposure in long and short positions in the variable Exposure. The bounds for individual asset weights are plus or minus Exposure. Since the net position must be dollar-neutral, the budget constraint is 0 and the initial portfolio must be 0. Finally, the one-way turnover constraints provide the necessary long and short restrictions to prevent “double-counting” of long and short positions.

%% dollar-neutral hedge-fund structure
Exposure=1;
q=setBounds(p, -Exposure, Exposure);
q=setBudget(q, 0, 0); % 组合总头寸必须为0，dollar neutral
q=setOneWayTurnover(q, Exposure, Exposure, 0); % one way turnover constraint(单向交易限制)[qwgt, qlong, qshort]=estimateFrontier(q, 20); % 有效前沿
[qrsk, qret]=estimatePortMoments(q, qwgt);[qswgt, qslong, qsshort]=estimateMaxSharpeRatio(q); % 最大Sharpe Ratio Point
[qsrsk, qsret]=estimatePortMoments(q, qswgt);portfolioexamples_plot('Efficient Frontier with Dollar-Neutral Portfolio', ...{'line', prsk, pret, {'Standard'}, 'b:'}, ...{'line', qrsk, qret, {'Dollar-Neutral'}, 'b'}, ...{'scatter', qsrsk, qsret, {'Max Sharpe Ratio Point'}}, ...{'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ...{'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

130/30 Fund Structure

使用turnover constraints建立130-30组合，净头寸为多头，但是允许加杠杆，在130-30策略中，杠杆率为30%

a structure with a net long position but premits leverage with long and short positions up to a maximum amount of leverage. In the case of a 130-30 portfolio, the leverage is 30%.

%% 130/30 Fund Structure
Leverage=0.3; % 130-30 structureq=setBounds(p, -Leverage, 1+Leverage);
q=setBudget(q, 1, 1); % 组合净头寸为 long 1
q=setOneWayTurnover(q, 1+Leverage, Leverage);[qwgt, qbuy, qsell]=estimateFrontier(q, 20); % 有效前沿
[qrsk, qret]=estimatePortMoments(q, qwgt);[qswgt, qslong, qsshort]=estimateMaxSharpeRatio(q); %Max Sharpe Ratio Point
[qsrsk, qsret]=estimatePortMoments(q, qswgt);% plot
portfolioexamples_plot(sprintf('Efficient Frontier with %g-%g Portfolio', ...100*(1 + Leverage),100*Leverage), ...{'line', prsk, pret, {'Standard'}, 'b:'}, ...{'line', qrsk, qret, {'130-30'}, 'b'}, ...{'scatter', qsrsk, qsret, {'Sharpe'}}, ...{'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ...{'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});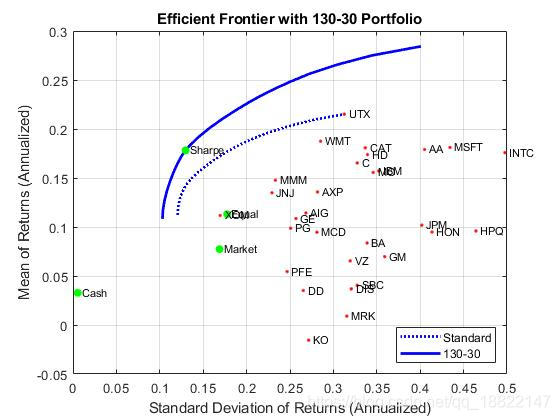

代码下载

porfolio example matlab code

参考资料

Matlab: Portfolio Optimization Examples
主动投资组合管理 R.C. Grinold & R.N. Kahn.
Mutual Fund Performance