RTKLIB学习（一）--spp代码分析

总纲：

        我计划对RTKLIB学习 的目标是掌握PPP流程与逻辑，但先掌握比较简单的spp定位对PPP的学习还是有一些帮助的，尤其先在spp熟悉一些共有的数据结构和rtcmn.c中大量重合的函数后，对PPP学习应该不会太难。

        本文内容先列出spp实现定位主要功能函数pntpos.c，在对其实现流程做大概阐述（并附上其他免费优秀博主的spp文章），重要的一环是对spp所用到的加权最小二乘（weighted least square）和一些矩阵运算进行较为详细的阐述。

一、流程概览

spp主要定位功能pntpos()函数概览

 pntpos()函数调用

 main.c/rnx2rtkp.c文件的main()函数中的postpos()函数--->postpos.c文件的postpos()中的execses_b()-->postpos.c文件的execses_b()中的execses_r()-->postpos.c文件的execses_r()中的

execses()-->postpos.c文件的execses()中的procpos()-->postpos.c文件的procpos()中的rtkpos()-->

rtkpos.c文件的rtkpos()中的pntpos()。

这篇文章相当详细

至此开始pntpos函数讲解。

 二、pntpos实现逻辑

下面这篇文章详细介绍了各级函数的调用及作用 

 参考链接：RTKLIB源码解析（一）——单点定位(pntpos.c) - 塔奇克马敲代码 - 博客园 (cnblogs.com)

务必投入大量时间了解各级函数！！！ （我就不做重复性的介绍工作了）

（1）satposs()

在ephemeris.c文件的的718行（不同版本略有差异）

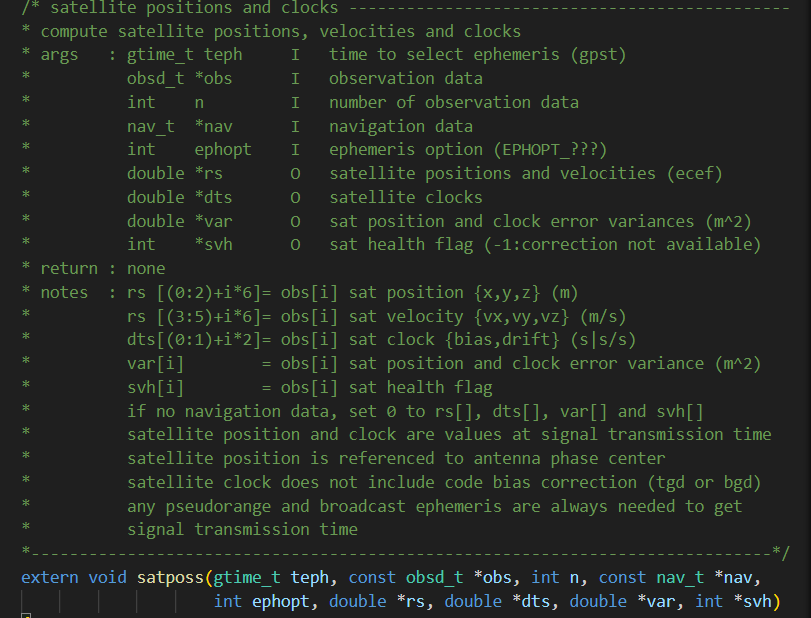
实现了通过广播星历（或者精密星历）计算卫星位置和钟差的功能

具体算法实现函数eph2pos()在ephemeris.c文件的181行左右

/* broadcast ephemeris to satellite position and clock bias --------------------
* compute satellite position and clock bias with broadcast ephemeris (gps,
* galileo, qzss)
* args   : gtime_t time     I   time (gpst)
*          eph_t *eph       I   broadcast ephemeris
*          double *rs       O   satellite position (ecef) {x,y,z} (m)
*          double *dts      O   satellite clock bias (s)
*          double *var      O   satellite position and clock variance (m^2)
* return : none
* notes  : see ref [1],[7],[8]
*          satellite clock includes relativity correction without code bias
*          (tgd or bgd)
*-----------------------------------------------------------------------------*/
extern void eph2pos(gtime_t time, const eph_t *eph, double *rs, double *dts,double *var)
{double tk,M,E,Ek,sinE,cosE,u,r,i,O,sin2u,cos2u,x,y,sinO,cosO,cosi,mu,omge;double xg,yg,zg,sino,coso;int n,sys,prn;trace(4,"eph2pos : time=%s sat=%2d\n",time_str(time,3),eph->sat);if (eph->A<=0.0) {rs[0]=rs[1]=rs[2]=*dts=*var=0.0;return;}tk=timediff(time,eph->toe);switch ((sys=satsys(eph->sat,&prn))) {case SYS_GAL: mu=MU_GAL; omge=OMGE_GAL; break;case SYS_CMP: mu=MU_CMP; omge=OMGE_CMP; break;default:      mu=MU_GPS; omge=OMGE;     break;}M=eph->M0+(sqrt(mu/(eph->A*eph->A*eph->A))+eph->deln)*tk;for (n=0,E=M,Ek=0.0;fabs(E-Ek)>RTOL_KEPLER&&n<MAX_ITER_KEPLER;n++) {Ek=E; E-=(E-eph->e*sin(E)-M)/(1.0-eph->e*cos(E));}if (n>=MAX_ITER_KEPLER) {trace(2,"kepler iteration overflow sat=%2d\n",eph->sat);return;}sinE=sin(E); cosE=cos(E);trace(4,"kepler: sat=%2d e=%8.5f n=%2d del=%10.3e\n",eph->sat,eph->e,n,E-Ek);u=atan2(sqrt(1.0-eph->e*eph->e)*sinE,cosE-eph->e)+eph->omg;r=eph->A*(1.0-eph->e*cosE);i=eph->i0+eph->idot*tk;sin2u=sin(2.0*u); cos2u=cos(2.0*u);u+=eph->cus*sin2u+eph->cuc*cos2u;r+=eph->crs*sin2u+eph->crc*cos2u;i+=eph->cis*sin2u+eph->cic*cos2u;x=r*cos(u); y=r*sin(u); cosi=cos(i);/* beidou geo satellite (ref [9]) */if (sys==SYS_CMP&&prn<=5) {O=eph->OMG0+eph->OMGd*tk-omge*eph->toes;sinO=sin(O); cosO=cos(O);xg=x*cosO-y*cosi*sinO;yg=x*sinO+y*cosi*cosO;zg=y*sin(i);sino=sin(omge*tk); coso=cos(omge*tk);rs[0]= xg*coso+yg*sino*COS_5+zg*sino*SIN_5;rs[1]=-xg*sino+yg*coso*COS_5+zg*coso*SIN_5;rs[2]=-yg*SIN_5+zg*COS_5;}else {O=eph->OMG0+(eph->OMGd-omge)*tk-omge*eph->toes;sinO=sin(O); cosO=cos(O);rs[0]=x*cosO-y*cosi*sinO;rs[1]=x*sinO+y*cosi*cosO;rs[2]=y*sin(i);}tk=timediff(time,eph->toc);*dts=eph->f0+eph->f1*tk+eph->f2*tk*tk;/* relativity correction */*dts-=2.0*sqrt(mu*eph->A)*eph->e*sinE/SQR(CLIGHT);/* position and clock error variance */*var=var_uraeph(eph->sva);
}

在各GPS测量书籍中都会有详细的公式。

（2）estpos()

在pntpos.c文件的309行左右，该函数的实现了计算接收机位置的功能。

estpos()函数包括了用于计算伪距残差的rescode()函数和用于计算接收机位置的加权最小二乘函数lsq()。也是本文后续着重介绍的函数。

（3）raim_fde()

在pntpos.c文件的377行左右，实现排除故障卫星并重新计算接收机位置的功能。

estpos()函数中，若解算结果不合格，即未通过卡方检验和最大GDOP值检验

在pntpos.c函数中通过调用raim_fde()函数，每次排除一颗卫星，然后重新定位（该函数只能实现故障卫星为一颗的情况）

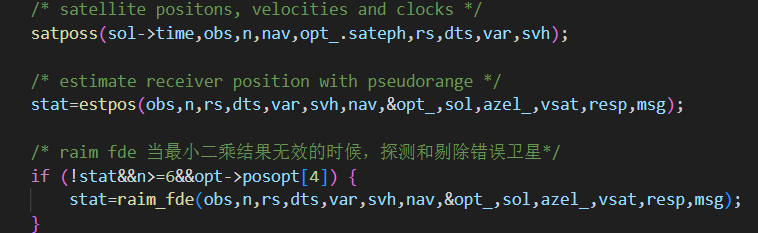
（4）estvel()

位于pntpos（）函数的第494行左右，实现了计算接收机速度的功能。

该函数利用resdop()函数计算多普勒频移残差，并用lsq()实现计算功能。

三、重点介绍加权最小二乘lsq()函数

1、对rtklib中的矩阵的必要知识

（1）矩阵定义与存储

        rtklib中的矩阵运算和无论是Python中的numpy矩阵运算库、MATLAB中的矩阵运算还是c++的Eigen矩阵运算库都不一样。

        从rtkcmn.c文件739行左右的extern double *mat(int n, int m)函数到1031行左右的lsq()函数都是和矩阵及spp定位相关功能的函数，在函数上面的注释中，也详细介绍了各函数的作用及参数。

/* new matrix ------------------------------------------------------------------
* allocate memory of matrix 
* args   : int    n,m       I   number of rows and columns of matrix
* return : matrix pointer (if n<=0 or m<=0, return NULL)
*-----------------------------------------------------------------------------*/
extern double *mat(int n, int m)
{double *p;if (n<=0||m<=0) return NULL;if (!(p=(double *)malloc(sizeof(double)*n*m))) {fatalerr("matrix memory allocation error: n=%d,m=%d\n",n,m);}return p;
}

        该函数实现通过参数n,m定义一个n行m列的矩阵，该函数通过指针p指向一块动态开辟的内存空间，并返回该指针作为矩阵存值空间。但仔细观察这段代码发现，malloc()开辟的是一维数组，也就是说，无论n,m是多少，指针所返回的是大小为（n*m）的一维数组。

        那举个例子说一个2*3的矩阵，

在指针p中存储顺序是不是应该为为（1,2,3,4,5,6），如果这样以为，那就大错特错了！

注意在rtklib中上面的矩阵存储为（1,4,2,5,3,6），也就是说按照列存储进行。也就是说一个n行m列矩阵的第i行j列的元素在一维矩阵数组中的是p[i-1+(j-1)*n]

（2）矩阵乘法 

 在matmul（）函数中实现矩阵乘法；传入参数分别为（转置标识符*tr，A矩阵的行n，B矩阵de列n，A矩阵的列m，A*B的缩放因子，左乘矩阵A,右乘矩阵B，C矩阵的缩放因子，结果矩阵C）

/* multiply matrix -----------------------------------------------------------*/
extern void matmul(const char *tr, int n, int k, int m, double alpha,const double *A, const double *B, double beta, double *C)
{double d;int i,j,x,f=tr[0]=='N'?(tr[1]=='N'?1:2):(tr[1]=='N'?3:4);//N标识符为不进行转置for (i=0;i<n;i++) for (j=0;j<k;j++) {d=0.0;switch (f) {case 1: for (x=0;x<m;x++) d+=A[i+x*n]*B[x+j*m]; break;case 2: for (x=0;x<m;x++) d+=A[i+x*n]*B[j+x*k]; break;case 3: for (x=0;x<m;x++) d+=A[x+i*m]*B[x+j*m]; break;case 4: for (x=0;x<m;x++) d+=A[x+i*m]*B[j+x*k]; break;}if (beta==0.0) C[i+j*n]=alpha*d; else C[i+j*n]=alpha*d+beta*C[i+j*n];}
}

 上述矩阵相关详细介绍请参考：RTKLIB——matmul(矩阵乘法函数）_matmul rtklib-CSDN博客

其他矩阵矩阵运算查看相应注释即可

2、对最小二乘的先行知识

 rtklib用到的加权最小二乘和测量平差中的间接平差逻辑上是一样，先回顾间接平差公式

可见，进行加权最小二乘只需系数阵B，权阵P，残差向量l

3、lsp（）加权最小二乘

先看lsq()函数，注释中也列出了其进行的矩阵运算规则

/* least square estimation -----------------------------------------------------
* least square estimation by solving normal equation (x=(A*A')^-1*A*y)
* args   : double *A        I   transpose of (weighted) design matrix (n x m)
*          double *y        I   (weighted) measurements (m x 1)
*          int    n,m       I   number of parameters and measurements (n<=m)
*          double *x        O   estmated parameters (n x 1)
*          double *Q        O   esimated parameters covariance matrix (n x n)
* return : status (0:ok,0>:error)
* notes  : for weighted least square, replace A and y by A*w and w*y (w=W^(1/2))
*          matirix stored by column-major order (fortran convention)
*-----------------------------------------------------------------------------*/
extern int lsq(const double *A, const double *y, int n, int m, double *x,double *Q)//Q为参数协因数阵
{double *Ay;int info;//A=B';y=l且A经过加权处理if (m<n) return -1;Ay=mat(n,1);matmul("NN",n,1,m,1.0,A,y,0.0,Ay); /* Ay=A*y */matmul("NT",n,n,m,1.0,A,A,0.0,Q);  /* Q=A*A' */if (!(info=matinv(Q,n))) matmul("NN",n,1,n,1.0,Q,Ay,0.0,x); /* x=Q^-1*Ay */free(Ay);return info;
}

        通过注释发现A矩阵就是上小节系数阵B的转置，y向量就是上小节观测值残差向量l，x则为结果矩阵兼参数改正数矩阵。结束了？当然还没有，仔细对比上小节，看着看着，我突然发现权阵P哪去了，没有权阵还叫什么加权最小二乘！

        要找到答案就先回到estpos（）函数中，答案就在下图

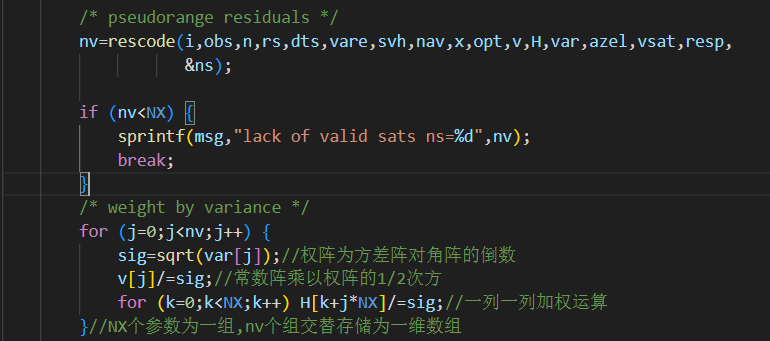
        在rescode()函数获取设计矩阵H，残差向量v后进行了weight by variance步骤，依次对v和H进行加权运算。仔细观察H的加权操作，便能验证之前矩阵赋值的结论。

for (j=0;j<NX;j++) x[j]+=dx[j];//参数平差值

这段代码获取参数平差值

if (norm(dx,NX)<1E-4) {//当参数改正数矩阵符合一定条件，则输出结果：sol->type=0;sol->time=timeadd(obs[0].time,-x[3]/CLIGHT);sol->dtr[0]=x[3]/CLIGHT; /* receiver clock bias (s) */sol->dtr[1]=x[4]/CLIGHT; /* glo-gps time offset (s) */sol->dtr[2]=x[5]/CLIGHT; /* gal-gps time offset (s) */sol->dtr[3]=x[6]/CLIGHT; /* bds-gps time offset (s) */for (j=0;j<6;j++) sol->rr[j]=j<3?x[j]:0.0;for (j=0;j<3;j++) sol->qr[j]=(float)Q[j+j*NX];sol->qr[3]=(float)Q[1];    /* cov xy */sol->qr[4]=(float)Q[2+NX]; /* cov yz */sol->qr[5]=(float)Q[2];    /* cov zx */sol->ns=(unsigned char)ns;sol->age=sol->ratio=0.0;/* validate solution *///valsol为结果有效性检验函数if ((stat=valsol(azel,vsat,n,opt,v,nv,NX,msg))) {sol->stat=opt->sateph==EPHOPT_SBAS?SOLQ_SBAS:SOLQ_SINGLE;}

进行结果输出操作和结果有效性检验

这篇文章主要内容已更新完毕，后续只会零零碎碎的添加一些spp相关知识，更多的精力还是放在了PPP上。

 此章未完，缓慢待更......