搞定了第二章。。。。
先上课件:Mathematics
Assignment 2: Mathematics
·1799 Yeehaa! (1)
简单平面几何证明,答案是r*sin(π/n)/(1+sin(π/n)),我就不需要证明了吧(不会的自己画图就可以证明,不过估计这个连初中生都会)。。。

 View Code
View Code #include <stdio.h> #include <math.h> #define PI 3.1415926int main() {int test,n,i;double r;scanf("%d",&test);for (i=1;i<=test;i++){printf("Scenario #%d:\n",i);scanf("%lf%d",&r,&n);printf("%.3lf\n",r*sin(PI/n)/(1+sin(PI/n)));printf("\n");}return 0; }
·1401 Factorial (1)
简单数论,直接套公式,答案是[n/5]+[n/5^2]+[n/5^3]+......。

 View Code
View Code #include <stdio.h>int main() {int test,n;int ans,tmp;scanf("%d",&test);while (test--){ans=0; tmp=5;scanf("%d",&n);while (n/tmp){ans+=n/tmp;tmp*=5;}printf("%d\n",ans);}return 0; }
·2262 Goldbach's Conjecture (2)
简单数论,筛出1000000以内的素数,然后枚举即可。。。

 View Code
View Code #include <stdio.h> #define MAXN 1000010int prime[MAXN]; int n;void sieve() {int i,j;for (i=1;i<MAXN;i++) prime[i]=1;for (i=2;i<MAXN;i++)if (prime[i]){for (j=i*2;j<MAXN;j+=i)prime[j]=0;} }int main() {int i,flag;sieve();while (scanf("%d",&n)!=EOF&&n){flag=0;for (i=3;i<=n/2;i++)if (prime[i]&&prime[n-i]){printf("%d = %d + %d\n",n,i,n-i);flag=1;break;}if (!flag) printf("Goldbach's conjecture is wrong.\n");}return 0; }
·2242 The Circumference of the Circle (2)
又是简单平面几何题——计算圆的周长。首先我们根据三点坐标可以求出三条边长a,b,c,利用余弦定理计算出CosA,然后计算出SinA,则直径D=a/SinA(这玩意叫正弦定理,不知道的回去把高中再读一次吧),然后周长C=π*D。

 View Code
View Code #include <stdio.h> #include <math.h> #define PI 3.141592653589793int main() {double x1,x2,x3;double y1,y2,y3;double a,b,c;double CosA;while (scanf("%lf%lf%lf%lf%lf%lf",&x1,&y1,&x2,&y2,&x3,&y3)!=EOF){a=sqrt((x2-x3)*(x2-x3)+(y2-y3)*(y2-y3));b=sqrt((x3-x1)*(x3-x1)+(y3-y1)*(y3-y1));c=sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1));CosA=(b*b+c*c-a*a)/(2*b*c);printf("%.2lf\n",PI*a/sqrt(1-CosA*CosA));}return 0; }
·1654 Area (3)
计算多边形面积,利用叉积即可计算,由于点给出的方向性未知,我们需要注意结果的正负,还有用int会溢出,要用long long,最后根据ans的奇偶判断是否在末尾加0.5。。

 View Code
View Code #include <stdio.h>typedef struct {long long x,y; }point;int main() {point pre,now;int test;long long ans;char cmd;scanf("%d\n",&test);while (test--){ans=0;pre.x=pre.y=0;while ((cmd=getchar())!='5'){switch (cmd){case '1':now.x=pre.x-1; now.y=pre.y-1; break;case '2':now.x=pre.x; now.y=pre.y-1; break;case '3':now.x=pre.x+1; now.y=pre.y-1; break;case '4':now.x=pre.x-1; now.y=pre.y; break;case '5':break;case '6':now.x=pre.x+1; now.y=pre.y; break;case '7':now.x=pre.x-1; now.y=pre.y+1; break;case '8':now.x=pre.x; now.y=pre.y+1; break;case '9':now.x=pre.x+1; now.y=pre.y+1; break;}ans+=now.y*pre.x-now.x*pre.y;pre=now;}if (now.x||now.y) ans=0;if (ans<0) ans=-ans;if (ans%2) printf("%I64d.5\n",ans/2);else printf("%I64d\n",ans/2);getchar();}return 0; }
·2309 BST (3)
就是找规律(规律太水了,一眼就能看出来,我就不废话),利用倍增的思想可以计算出结果,注意数据范围,int可能会溢出。。。

 View Code
View Code #include <stdio.h>int min,max;void find(int x) {long long delta;delta=1;while (delta*2<=x) delta*=2;if (delta!=x) delta=x-delta;delta=(delta & -delta)/2;min=max=x;while (delta){min-=delta;max+=delta;delta/=2;} }int main() {int n,x;scanf("%d",&n);while (n--){scanf("%d",&x);find(x);printf("%d %d\n",min,max);}return 0; }
·2693 Chocolate Chip Cookies (4)
计算几何,枚举两个点计算出圆心,然后枚举所有点,判断是否在圆内。。。
不知道如何求圆心的可以看下一段,知道的无视这一段。。。
先给出一个图:
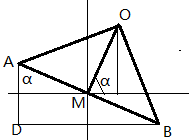
设A,B点坐标分别为(x1,y1),(x2,y2),M为AB中点,坐标为(x0=(x1+x2)/2,y0=(y1+y2)/2),OM⊥AB。我们可以求出OM的长度,设为h(怎么求我就不用说了)。显然O点的坐标就是(x0+hcosα,y0+hsinα)。下面介绍如何求解α,由图可知tanα=BD/AD,即tanα=(x2-x1)/(y1-y2),利用反三角函数α就出来了。。
需要注意的是精度问题和边界处理问题,还有半径是2.5,不是5.0(我在这里WA了好多次)

 View Code
View Code #include <stdio.h> #include <math.h> #define MAXN 210 #define e 1e-6 #define PI 3.1415926 #define R 2.5typedef struct {double x,y; }point;point a[MAXN]; int n=0;double dis(point a,point b) {return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); }point find(point a,point b) {point d,m,o;double alpha,h;m.x=(a.x+b.x)/2.0; m.y=(a.y+b.y)/2.0;d.x=b.x-a.x; d.y=a.y-b.y;if (fabs(d.y)<e) alpha=PI/2;else alpha=atan(d.x/d.y);h=sqrt(R*R-dis(a,m)*dis(a,m));o.x=m.x+h*cos(alpha);o.y=m.y+h*sin(alpha);return o; }int main() {int i,j,k;int ans=1;int count;point center;while (scanf("%lf%lf",&a[n].x,&a[n].y)!=EOF)n++;for (i=0;i<n;i++)for (j=0;j<n;j++){if (i==j) continue;if (dis(a[i],a[j])-R*2>e) continue;center=find(a[i],a[j]);if (fabs(center.x-R)<e) continue;if (fabs(center.y-R)<e) continue;if (center.x+R>50) continue;if (center.y+R>50) continue;count=0;for (k=0;k<n;k++)if (dis(center,a[k])-R<=e) count++;if (count>ans) ans=count;}printf("%d\n",ans);return 0; }
·2084 Game of Connections (4)
简单组合数学,就是求Catalan Number,答案是C(2n,n)/(n+1),具体证明我也不太会。注意筛法求素数时,要筛到200。

 View Code
View Code #include <stdio.h> #include <stdlib.h> #include <string.h> #define SIZE 10000 #define MAXN 200int n,m; int a[SIZE]; int p[MAXN]; int c[MAXN];void get_prime() {int i,j;m=0;memset(p,1,sizeof(p));for (i=2;i<MAXN;i++)if (p[i]){p[m++]=i;for (j=i+i;j<MAXN;j+=i)p[j]=0;} }void mul(int n) {int i,x=0;for (i=1;i<=a[0];i++){a[i]=a[i]*n+x;x=a[i]/10;a[i]=a[i]%10;}while (x){a[0]++;a[a[0]]=x%10;x=x/10;} }int main() {int i,j;get_prime();while (scanf("%d",&n)&&n>0){memset(a,0,sizeof(a));a[0]=a[1]=1;memset(c,0,sizeof(c));for (i=0;i<m;i++){j=p[i];while (2*n/j){c[i]+=2*n/j;c[i]-=n/j+(n+1)/j;j*=p[i];}}for (i=0;i<m;i++)for (j=1;j<=c[i];j++)mul(p[i]);for (i=a[0];i>0;i--)printf("%d",a[i]);printf("\n");}return 0; }
·2085 Inversion (5)
这道题目挺不错的。。利用了组合数学和贪心的方法,如果我们知道每一个数逆序数,那么这个数列就确定了(这个十分显然,我就不多加证明)。。。
我们来考虑N=4,M=5这个例子。
首先,如果所求序列以1为首,则1的逆序为0,可以得出此时序列的逆序数最多为2+1=3<5,不满足。考虑以2为首,序列的逆序最多为3+1<5,不满足。考虑以3为首,可见当1的逆序为3,2的逆序为2,4的逆序为0时满足要求,这时1,2,4均为最大逆序,因而只能排列为4,2,1,加上首数,所求序列为3,4,2,1。若M=3,采取同样的贪心策略,可求得结果为1,4,3,2。依此思路,可以得到所求序列关于N,M的关系式,具体如下:1,2,3,...N-P, N-((p-1)*p/2-M), N , N-1...N-P+1.(P是满足(P-1)*P/2>=M的最小值)。
这个证明也是比较简单的,在此略去。。

 View Code
View Code #include <stdio.h>int n,m;int main() {int i,p,tmp;while (scanf("%d%d",&n,&m)&&n!=-1){p=1;while (p*(p-1)/2<m) p++;tmp=p*(p-1)/2;for (i=1;i<=n-p;i++)printf("%d ",i);printf("%d ",n-tmp+m);for (i=n;i>n-p;i--)if (i!=n-tmp+m)printf("%d ",i);printf("\n");}return 0; }
·1426 Find The Multiple (6)
考察了mod的应用和简单广搜。我们以余数为状态进行广搜,并记录就可以了。

 View Code
View Code #include <stdio.h> #include <stdlib.h> #include <string.h> #define MAXN 210 #define SIZE 10010int vis[MAXN]; int que[SIZE]; int bit[SIZE]; int pre[SIZE]; int head,tail; int n;void expand(int b) {int now;now=(que[head]*10+b)%n;if (!vis[now]){tail++;que[tail]=now;bit[tail]=b;pre[tail]=head;vis[now]=1;} }void bfs() {memset(vis,0,sizeof(vis));vis[1]=que[1]=bit[1]=1; pre[1]=0;head=tail=1;while (head<=tail){if (que[head]==0) break;expand(0);expand(1);head++;} }void print(int n) {if (!n) return;print(pre[n]);printf("%d",bit[n]); }int main() {while (scanf("%d",&n)!=EOF&&n){bfs();print(head);printf("\n");}return 0; }
·2356 Find a multiple (7, challenge problem)
容斥原理即可解决这道题目。首先我们令sum[i]=(a[1]+a[2]+…+a[i])%N,显然sum[i]的取值范围在0到N-1之间。如果Nsum[i]中有一个为零,那么数列a[1],a[2],...,a[i]就满足了条件;如果不存在sum[i]=0,那么根据容斥原理,必存在i<j,使得sum[i]=sum[j],这时候(a[i+1]+a[i+1]+...+a[j])%N=0,我们就构造出了满足条件的另一个序列。

 View Code
View Code #include <stdio.h> #include <stdlib.h> #include <string.h> #define MAXN 10010int sum[MAXN],a[MAXN]; int pos[MAXN]; int n;int main() {int i,j;while (scanf("%d",&n)!=EOF){sum[0]=0;for (i=1;i<=n;i++){scanf("%d",&a[i]);sum[i]=(sum[i-1]+a[i])%n;}memset(pos,-1,sizeof(pos));for (i=0;i<=n;i++)if (pos[sum[i]]!=-1){printf("%d\n",i-pos[sum[i]]);for (j=pos[sum[i]]+1;j<=i;j++)printf("%d\n",a[j]);break;}else pos[sum[i]]=i;}return 0; }
·1148 Utopia Divided (9, challenge problem)
又是难度为9的题目,看了半天没有头绪,看了题解还是不懂,以后再来补上。。。。