孤立随机森林算法

孤立森林（Isolation Forest）算法是西瓜书作者周志华老师的团队研究开发的算法，一般用于结构化数据的异常检测。

异常的定义

针对于不同类型的异常，要用不同的算法来进行检测，而孤立森林算法主要针对的是连续型结构化数据中的异常点。

使用孤立森林的前提是，将异常点定义为那些 “容易被孤立的离群点” —— 可以理解为分布稀疏，且距离高密度群体较远的点。从统计学来看，在数据空间里，若一个区域内只有分布稀疏的点，表示数据点落在此区域的概率很低，因此可以认为这些区域的点是异常的。

也就是说，孤立森林算法的理论基础有两点：

• 异常数据占总样本量的比例很小；
• 异常点的特征值与正常点的差异很大。
  
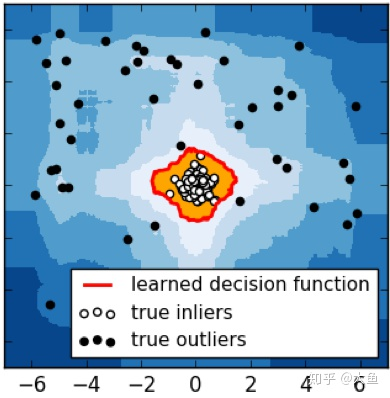
  上图中，中心的白色空心点为正常点，即处于高密度群体中。四周的黑色实心点为异常点，散落在高密度区域以外的空间。

使用场景

孤立森林算法是基于 Ensemble 的异常检测方法，因此具有线性的时间复杂度。且精准度较高，在处理大数据时速度快，所以目前在工业界的应用范围比较广。常见的场景包括：网络安全中的攻击检测、金融交易欺诈检测、疾病侦测、噪声数据过滤（数据清洗）等。

与其他异常检测算法的差异

孤立森林中的 “孤立” (isolation) 指的是 “把异常点从所有样本中孤立出来”，论文中的原文是 “separating an instance from the rest of the instances”.

大多数基于模型的异常检测算法会先 ”规定“ 正常点的范围或模式，如果某个点不符合这个模式，或者说不在正常范围内，那么模型会将其判定为异常点。

孤立森林的创新点包括以下四个：

1. Partial models：在训练过程中，每棵孤立树都是随机选取部分样本；
2. No distance or density measures：不同于 KMeans、DBSCAN 等算法，孤立森林不需要计算有关距离、密度的指标，可大幅度提升速度，减小系统开销；
3. Linear time complexity：因为基于 ensemble，所以有线性时间复杂度。通常树的数量越多，算法越稳定；
4. Handle extremely large data size：由于每棵树都是独立生成的，因此可部署在大规模分布式系统上来加速运算。

算法思想

想象这样一个场景，我们用一个随机超平面对一个数据空间进行切割，切一次可以生成两个子空间（也可以想象用刀切蛋糕）。接下来，我们再继续随机选取超平面，来切割第一步得到的两个子空间，以此循环下去，直到每子空间里面只包含一个数据点为止。

直观上来看，我们可以发现，那些密度很高的簇要被切很多次才会停止切割，即每个点都单独存在于一个子空间内，但那些分布稀疏的点，大都很早就停到一个子空间内了。

训练-测试过程

单棵树的训练

1 从训练数据中随机选择 Ψ 个点作为子样本，放入一棵孤立树的根节点；
2 随机指定一个维度，在当前节点数据范围内，随机产生一个切割点 p —— 切割点产生于当前节点数据中指定维度的最大值与最小值之间；
3 此切割点的选取生成了一个超平面，将当前节点数据空间切分为2个子空间：把当前所选维度下小于 p 的点放在当前节点的左分支，把大于等于 p 的点放在当前节点的右分支；
4 在节点的左分支和右分支节点递归步骤 2、3，不断构造新的叶子节点，直到叶子节点上只有一个数据（无法再继续切割） 或树已经生长到了所设定的高度 。（至于为什么要对树的高度做限制，后续会解释）

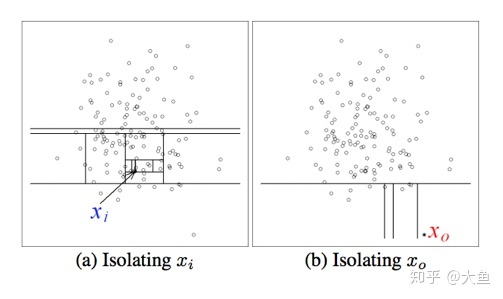
上图就是对子样本进行切割训练的过程，左图的xi 处于密度较高的区域，因此切割了十几次才被分到了单独的子空间，而右图的 x0落在边缘分布较稀疏的区域，只经历了四次切分就被 “孤立” 了。

整合全部孤立树的结果

由于切割过程是完全随机的，所以需要用 ensemble 的方法来使结果收敛，即反复从头开始切，然后计算每次切分结果的平均值。

获得 t 个孤立树后，单棵树的训练就结束了。接下来就可以用生成的孤立树来评估测试数据了，即计算异常分数 s。 对于每个样本 x，需要对其综合计算每棵树的结果，通过下面的公式计算异常得分：

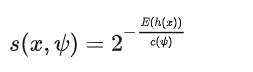
h(x) 为 x 在每棵树的高度，c(Ψ) 为给定样本数 Ψ 时路径长度的平均值，用来对样本 x 的路径长度 h(x) 进行标准化处理。

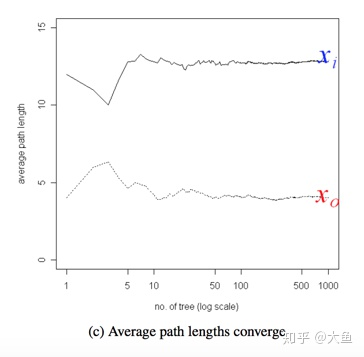
上图为孤立树的数目与每个样本点的平均高度的关系，可以看到数目选取在 10 以内时，结果非常不稳定，当数目达到 100 后就趋于收敛了。因此我们在使用过程中，树的棵树设置为 100 即可，如果棵树过少结果可能不稳定，若过多则白白浪费了系统开销。

异常得分

如果异常得分接近 1，那么一定是异常点；

如果异常得分远小于 0.5，那么一定不是异常点；

如果异常得分所有点的得分都在 0.5 左右，那么样本中很可能不存在异常点。

总结

孤立森林算法总共分两步：

• 训练 iForest：从训练集中进行采样，构建孤立树，对森林中的每棵孤立树进行测试，记录路径长度；
• 计算异常分数：根据异常分数计算公式，计算每个样本点的 anomaly score。
  两个坑

在使用孤立森林进行实际异常检测的过程中，可能有两个坑：

• 若训练样本中异常样本的比例较高，可能会导致最终结果不理想，因为这违背了该算法的理论基础；
• 异常检测跟具体的应用场景紧密相关，因此算法检测出的 “异常” 不一定是实际场景中的真正异常，所以在特征选择时，要尽量过滤不相关的特征。

一个生动的例子

因为我比较喜欢武林外传，而且这部剧中每个人的特点都很鲜明，所以拿过来做例子。以下是 9 位主要角色的基本数据：

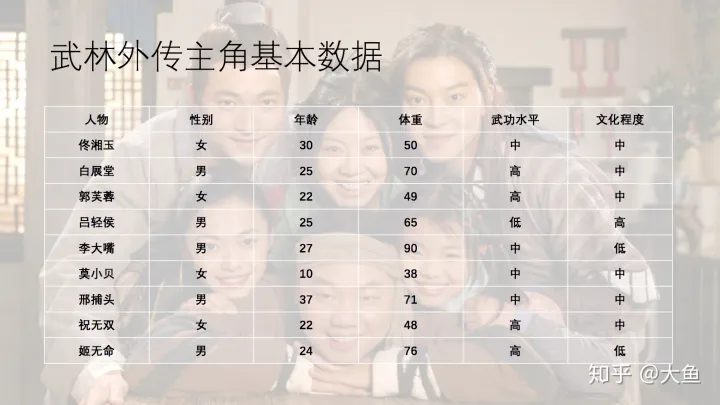
接下来，我们模拟一棵孤立树的训练过程，把这九个人作为一个子样本放入一棵孤立树的根节点：

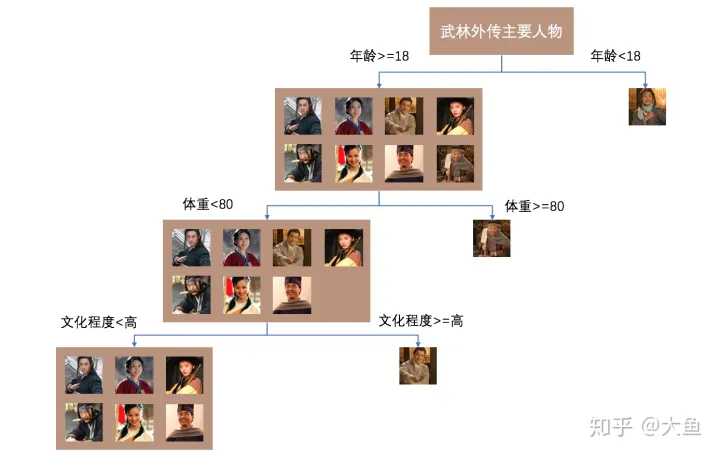
首先随机选择到的维度是 “年龄”，然后随机选择一个切割点 18，小于 18 岁的只有莫小贝一个人，所以她最先被 “孤立” 出来了；第二个随机选择的特征是 ”体重“，只有大嘴高于 80 公斤，所以也被 ”孤立“ 了；第三个选择 ”文化程度“ 这个特征，由于只有秀才的文化程度为高，于是被 ”孤立“ 出来了 ……

假设我们设定树的高度为 3，那么这棵树的训练就结束了。在这棵树上，莫小贝的路径长度为 1，大嘴为 2，秀才为 3，单看这一棵树，莫小贝的异常程度最高。但很显然，她之所以最先被孤立出来，与特征被随机选择到的顺序有关，所以我们通过对多棵树进行训练，来去除这种随机性，让结果尽量收敛。