详细解读论文 CPC：Representation Learning with Contrastive Predictive Coding

Abstract:

​该篇论文提出了一种完全的无监督的方法，旨在从高维的特征空间中提取有效特征同时舍弃掉一些更加局部的特征。简单来说目的就是更加有效的提取特征，提取更加global的"slow features"。该方法较为通用，在很多任务中都可以得到应用，文中列举了：语音，图像，文本，3D领域强化学习等方向的应用。

Method:

​无监督学习并没有label来引导网络学习，就像一个野外长大的孩子，没有大人教他何为对错，只能从不断接触到的新的环境中寻找规律。为了提取到前面描述的“良好的“特征，该篇论文的方法是：增大当前状态特征c与未来输入特征x的互信息。为什么要这么做呢？如果我能用当前的输入在一定程度上去”预测“后面的输入，那么我就已经找到了输入的某些规律，也就是提取到的特征能够很好的描述输入数据的一些共同之处。

​那么如何衡量特征间的互信息呢？用x指代输入，用c指代上下文，文中指出假如仅仅用p(x|c)来代表互信息不是最优的。因为使用这种条件概率衡量互信息有一个弊端：例如对于图像，这里的高维特征c所含的信息是要远少于输入图像的信息量的，这样来衡量当前状态特征c与未来输入x的互信息并不是最优的。我的理解是：由于c自身所携带的信息较小，所以当以优化条件概率p(x|c)为目的的模型在训练时可能导致用c预测的x会忽略一些信息。取而代之文中使用下式来衡量x和c的互信息大小：

这个式子可以说是本文的核心。至于为何使用log函数中类似概率密度的形式，后面会有解释。

如图所示，zt为encoder的输出，ct为自回归模型当前时刻的输出。

​有了这个式子，关键就在于如何表示 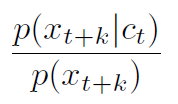这个概率密度，这里就有了一个很难理解的函数：

这里的Wk为一个转换矩阵使得Wkct 与encoder编码x后得到的特征z形状相同，对预测的每一个步长k都有一个对应的Wk。

这个函数满足

文中提到，其实任意正实函数都可作为这个fk函数使用，如何理解这个正实呢，我的直观的理解是当encoder已经能够很好的提取特征时，对xt+k提取的特征zt+k和Wkct更相似时这个函数就越大即可。那么为什么这样的一个正实函数就能正比于前面提出的概率密度呢？

首先论文提出了一个基于NCE的损失函数，把它称作InfoNCE:

​其中X={x1,…,xN}为包含一个从分布p(x|c)采样得到的正样本以及N-1个从分布p(x)中采样得到的负样本。对于这里正负样本的含义我的理解是，从前者条件概率分布中采样得到的正样本代表以我现在及过去输入信息的特征ct为条件距现在k个步长的真实输入，而负样本则是我想让网络学习提取特征的这一堆输入之外的其他的输入，这个输入可以是任意的。

​文中说只要优化这个损失函数就能使最终优化好的模型满足 这个式子，证明如下：

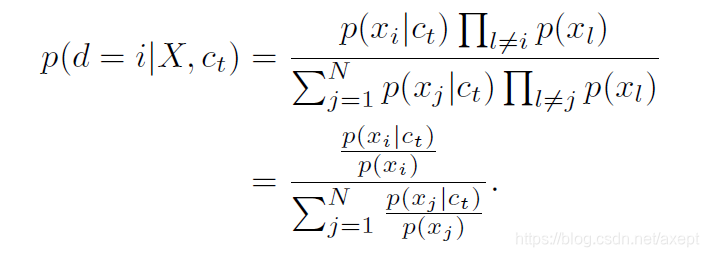
​这里等式左边代表在N个输入中xi是来自分布p(x|c)的正样本概率，这个概率即为InfoNCE的最优概率，可以简单理解为优化InfoNCE就是要让这个概率尽量大。这里第一个等号较难理解，等式右边分子代表N个样本中，xi为来自分布p(x|c)的正样本，其余N-1个样本为来自分布p(x)的负样本的概率；分母代表x1,x2,…,xN是来自分布p(x|c)的正样本概率之和。打个比方，这个概率的意义类似于，已知我们之间有一个叛徒，这个叛徒是第i个人的概率。第二个等号就是分子分母约分的结果。

​对比化简后的式子和InfoNCE可以发现优化后的f满足正比于之前的概率密度，即得证。

我们可以估计出，xt+k和ct之间的互信息满足：

可以看出当样本数N增大时，该互信息的下界增大，又因为每个batch中正样本只有一个，所以负样本越多，这个互信息的下界越大。

Experiments：

文中列举了cpc在4个领域的应用，在这里只简单介绍下audio的实验结果，具体实验设置文中有详细描述。

​由左表中可以看出，在语音识别的两项任务中，特别是speaker classification任务中，cpc这种无监督的方法的准确率已经十分接近监督学习的方法。右表展示了预测步长以及负样本采样对结果的影响。

Summary：

​CPC是一种完全无监督的训练特征提取的方法，它的可移植性很强，能适用于多种任务，效果上在很多任务中能够媲美甚至超越现有的监督方法。