消防车调度问题：用数学建模优化生产与服务运作中的管理问题

本文主要是介绍消防车调度问题：用数学建模优化生产与服务运作中的管理问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

问题描述：某市消防中心同时接到了三处火警电话。根据当前的火势，三处火警地点分别需要 2 辆、2 辆和 3 辆消防车前往灭火。三处火警地点的损失将依赖于消防车到达的及时程度：记 $t_{ij}$ 为第 j 辆消防车到达火警地点i的时间，则三处火警地点的损失分别为

$6t_{11}+4t_{12};\: 7t_{21}+3t_{22};\: \: 9t_{31}+8t_{32}+5t_{33}$ ; 。目前可供消防中心调度的消防车正好有 7辆，分别属于三个消防站（可用消防车数量分别为 3 辆、2 辆、2 辆）。消防车从三个消防站到三个火警地点所需要的时间如表 6 所示。应如何调度消防车，才能使总损失最小？

问题二：如果三处火警地点的损失分别为 $4t_{11}+6t_{12};\: 3t_{21}+7 t_{22};\: \: 5t_{31}+8t_{32}+9t_{33}$ ；，调度方案是否需要改变？

（1）问题分析

本题考虑的是为每个火警地点分配消防车的问题，初步看来与线性规划中经典的运输问题有些类似。本题的问题可以看成是指派问题和运输问题的一种变形，我们下面首先把它变成一个运输问题建模求解。

（2）决策变量

为了用运输问题建模求解，我们很自然地把 3 个消防站看成供应点。如果直接把 3 个火警地点看成需求点，我们却不能很方便地描述消防车到达的先后次序，因此难以确定损失的大小。下面我们把 7 辆车的需求分别看成 7 个需求点（分别对应于到达时间 $t_{11},\: t_{12},\: \: t_{21},\: t_{22},\: \: t_{31},\: t_{32},\: t_{33}$ . 用 $x_{ij}$ 表示消防站i是否向第 j 个需求点派车（1 表示派车，0表示不派车），则共有 21 个 0−1 变量.

（3）模型建立

题目中给出的损失函数都是消防车到达时间的线性函数，所以由所给数据进行简单的计算可知，如果消防站 1 向第 6 个需求点派车（即消防站 1 向火警地点 3 派车但该消防车是到达火警地点 3 的第二辆车），则由此引起的损失为 72 98 = × 。同理计算，可以得到损失矩阵如表 7 所示（元素分别记为 $c_{ij}$ ）。

于是，使总损失最小的决策目标为

$\textup{min}\:\: \: Z=\sum_{i=1}^{3}\sum_{j=1}^{7}c_{ij}\, x_{ij}$ ( 1 )

约束条件：

约束条件有两类，一类是消防站拥有的消防车的数量限制，另一类是各需求点对消防车的需求量限制。
记 $b_{i}$ （ i=1,2,3 ）为第i个消防站拥有消防车的数量，则消防站拥有的消防车的数量限制可以表示为
$\sum_{j=1}^{7} x_{ij} =b_{i} ,\: \: i=1,2,3$ ( 2 )

各需求点对消防车的需求量限制可以表示为

$\sum_{i=1}^{3} x_{ij} =1 ,\: \: j=1,2,...,7$ ( 3 )

（4）模型求解的lingo代码

MODEL: 
TITLE 消防车问题; 
SETS: 
supply/1..3/:b; 
need/1..7/; 
links(supply,need):c,x; 
ENDSETS 
[OBJ]Min=@sum(links:c*x); 
@FOR(supply(i):@sum(need(j):x(i,j))=b(i)); 
@FOR(need(j):@sum(supply(i):x(i,j))=1); 
DATA: 
b=3,2,2; 
c=36,24,49,21,81,72,45   30,20,56,24,99,88,55   36,24,63,27,90,80,50; 
ENDDATA 
END

求得结果为，消防站 1 应向火警地点 2 派 1 辆车，向火警地点 3 派 2 辆车；消防站 2 应向火警地点 1 派 2 辆车；消防站 3 应向火警地点 2、3 各派 1 辆车。最小总损失为 329。

（5）讨论

1）这个问题本质上仍然和经典的运输问题类似，可以把每辆车到达火场看做需求点，消防站看做供应点。在上面模型中，我们虽然假设 $x_{ij}$ 为 0− 1变量，但求解时是采用线性规划求解的，也就是说没有加上为 0− 1 变量或整数变量的限制条件，但求解得到的结果中 $x_{ij}$ 正好是 0−1 变量。这一结果不是偶然的，而是运输问题特有的一种性质.

2 ）在上面模型中，没有考虑消防车到达各火警地点的先后次序约束，但得到的结果正好满足所有的先后次序约束，这一结果不是必然的，而只是巧合。如对例题后半部分的情形，结果就不是这样了。显然，此时只需要修改损失矩阵如表 8 所示（所示（元素仍然分别记为 $c_{ij}$ )

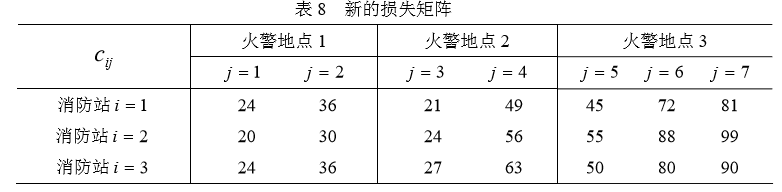
此时重新将式（ 1 )-( 3 ) 构成的线性规划模型输入 LINGO 求解，可以得到新的最优解： $x_{14 }=x_{16 }=x_{17 }=x_{21 }=x_{22 }=x_{ 33}=x_{35 }=1$ 其它变量为 0（最小总损失仍为 329）

实际上，损失矩阵中只是 1、2 列交换了位置，3、4 列交换了位置，5、7 列交换了位置，因此不用重新求解就可以直接看出以上新的最优解。

但是，以上新的最优解却是不符合实际情况的。例如， $x_{14}=x_{33}=1$ 表明火警地点2 的第一辆消防车来自消防站 3，第二辆消防车来自消防站 1，但这是不合理的，因为火警地点 2 与消费站 3 有 9min 的距离，大于与消防站 1 的 7min 的距离。分配给火警地点 3 的消防车也有类似的不合理问题。为了解决这一问题，我们必须考虑消防车到达各火警地点的先后次序约束，也就是说必须在简单的运输问题模型中增加一些新的约束，以保证以上的不合理问题不再出现。

首先考虑火警地点 2。由于消防站 1 的消防车到达所需时间（7min）小于消防站 2 的消防车到达所需时间（8 分钟），并都小于消防站 3 的消防车到达所需时间（9 分钟），因此火警地点 2 的第二辆消防车如果来自消防站 1，则火警地点 2 的第 1 辆消防车也一定来自消防站 1；火警地点 2 的第 2 辆消防车如果来自消防站 2，则火警地点 2 的第 1 辆消防车一定来自消防站 1 或 2。因此，必须增加以下约束： $x_{14} < x_{33}, \: x_{24}\leq x_{13} +x_{23}$ ( 4 )

同理，对火警地点 1，必须增加以下约束: $x_{22}\leq x_{21}$ ( 5 )

对火警地点 3，必须增加以下约束: $x_{16}\leq x_{15},\, x_{17}\leq x_{16},\: x_{36}\leq x_{15} + x_{35},\, 2x_{37}\leq x_{15} + x_{16}+ x_{35}+ x_{36}$ ( 6 )

重新将式（1）～（6）构成的整数规划模型（ $x_{ij}$ 是 1 0− 变量）输入 LINGO 软件如下:

MODEL: 
TITLE 消防车问题; 
SETS: 
supply/1..3/:b; 
need/1..7/; 
links(supply,need):c,x; 
ENDSETS 
[OBJ]Min=@sum(links:c*x); 
@FOR(supply(i):@sum(need(j):x(i,j))=b(i)); 
@FOR(need(j):@sum(supply(i):x(i,j))=1); 
x(1,4)<x(1,3); 
x(2,4)<x(1,3)+x(2,3); 
x(2,2)<x(2,1); 
x(1,6)<x(1,5); 
x(1,7)<x(1,6); 
x(3,6)<x(1,5)+x(3,5); 
2*x(3,7)<x(1,5)+x(1,6)+x(3,5)+x(3,6); 
@for(links:@bin(x)); 
DATA:
b=3,2,2; 
c=  24    36    21    49    45    72    81     20    30    24    56    55    88    99     24    36    27    63    50    80    90; 
ENDDATA 
END

求解可以得到： $x_{ 13} =x_{ 14}=x_{ 15}=x_{21 }=x_{ 22}=x_{ 36}=x_{ 37}=1$ ，其它变量为 0（最小总损失仍为 335）。也就是说，消防站 1 应向火警地点 2 派 2 辆车，向火警地点 3 派 1 辆车；消防站 2 应向火警地点 1 派 2 辆车；消防站 3 应向火警地点 3 派 2 辆车。经过检验可以发现，此时的派车方案是合理的。