本文主要是介绍【Python数据结构与算法】--- 递归算法应用-五行代码速解汉诺塔问题.,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

🌈个人主页: Aileen_0v0
🔥系列专栏:PYTHON数据结构与算法学习系列专栏
💫"没有罗马,那就自己创造罗马~"
汉诺塔
两层汉诺塔的演示
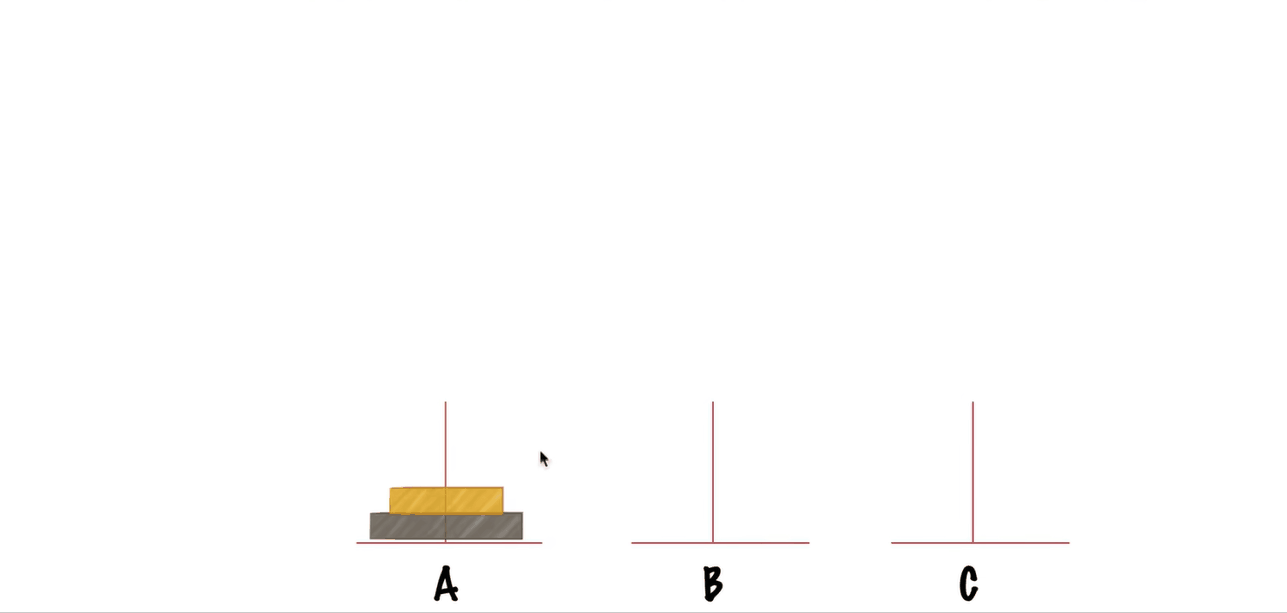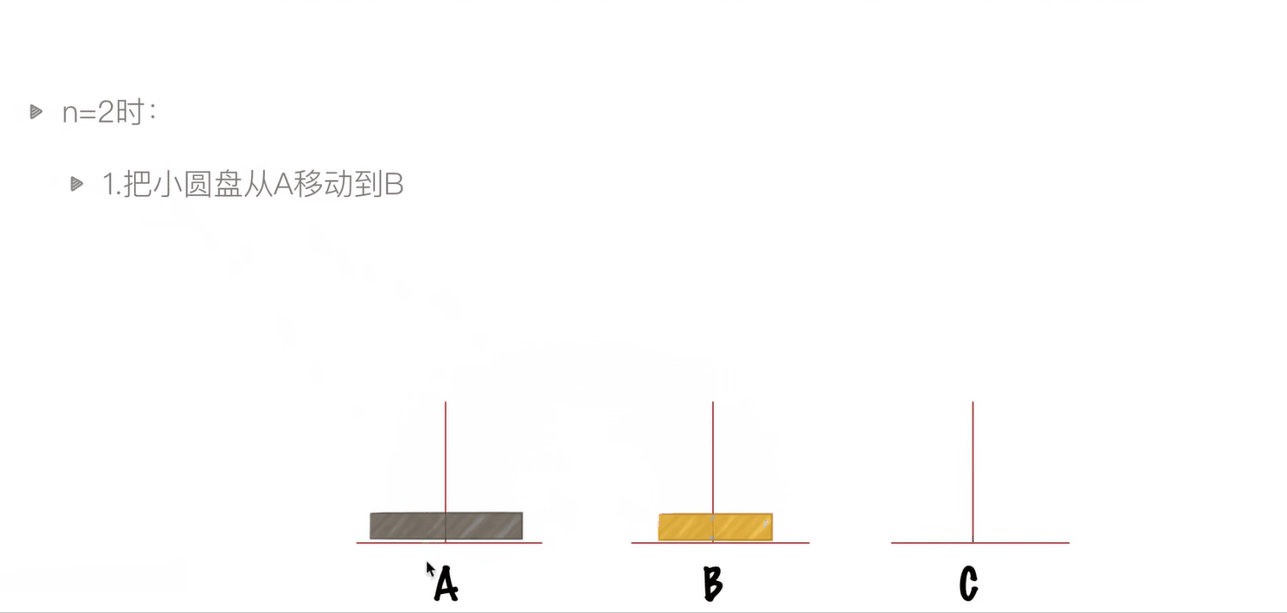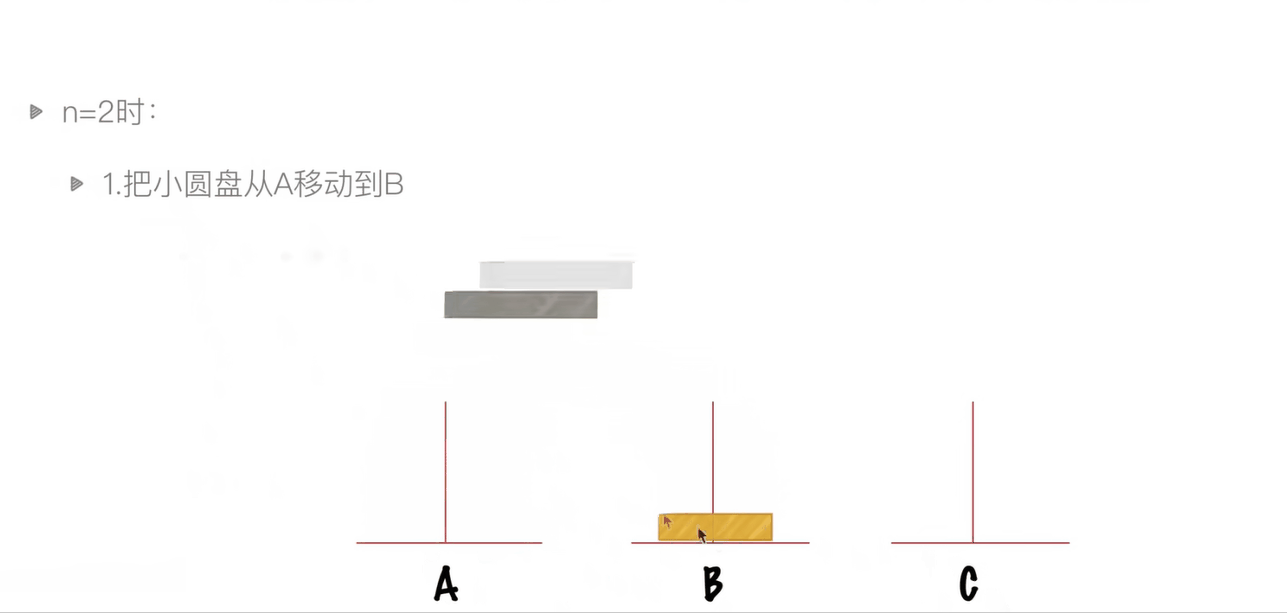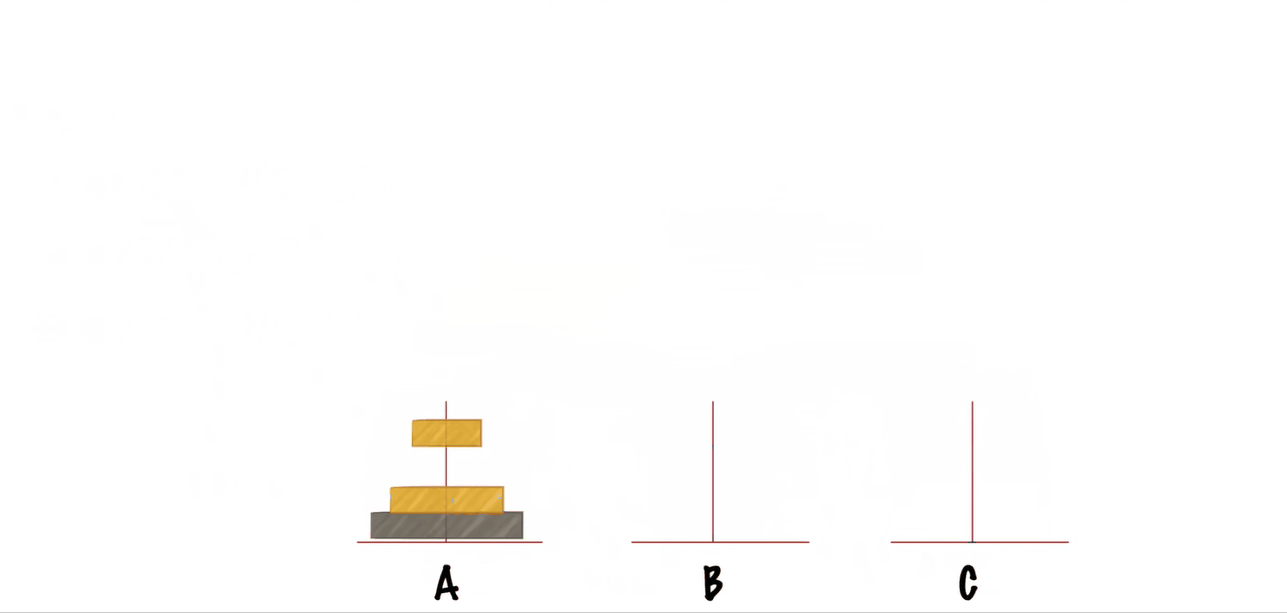

三层汉诺塔的走法演示
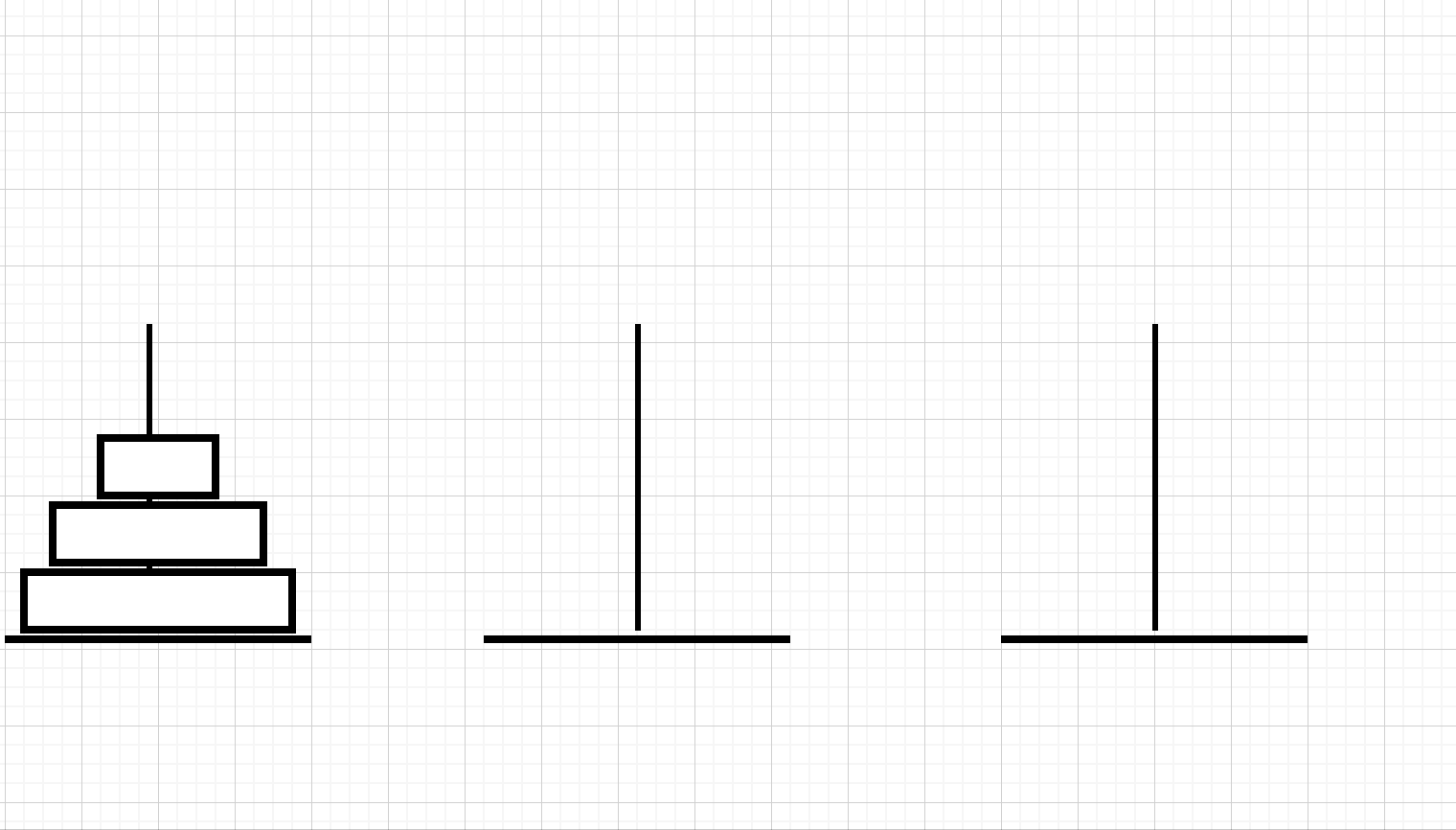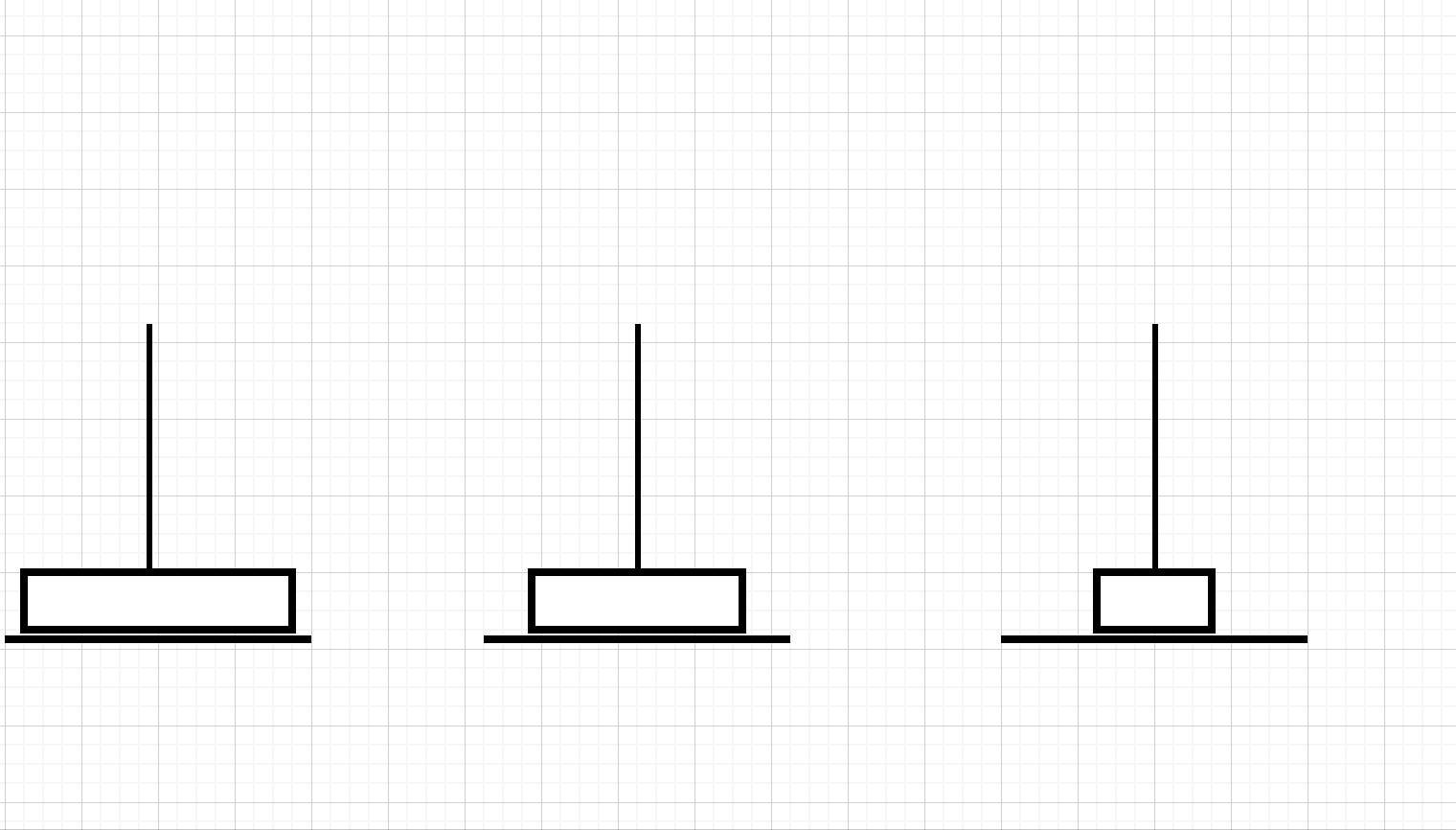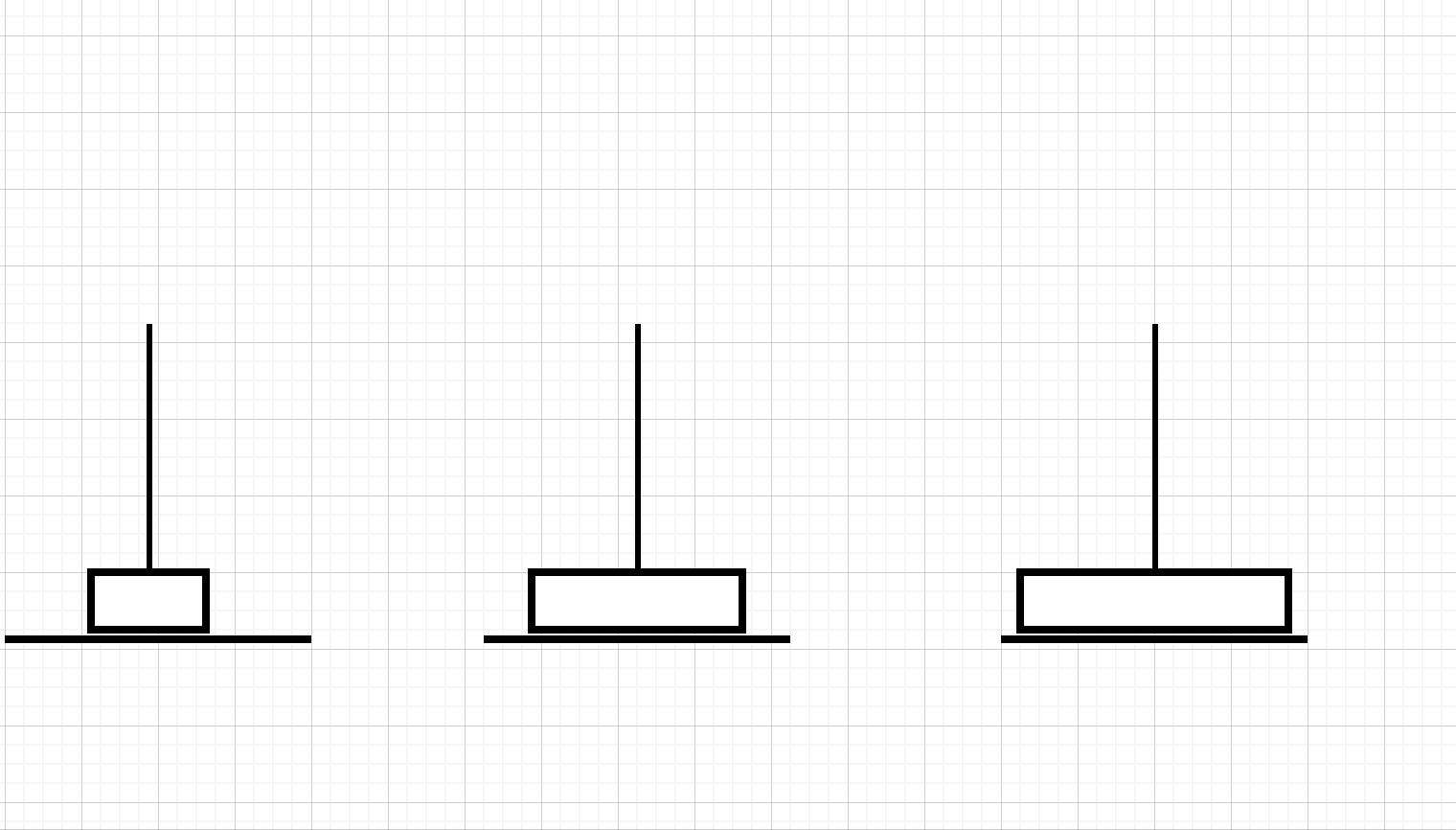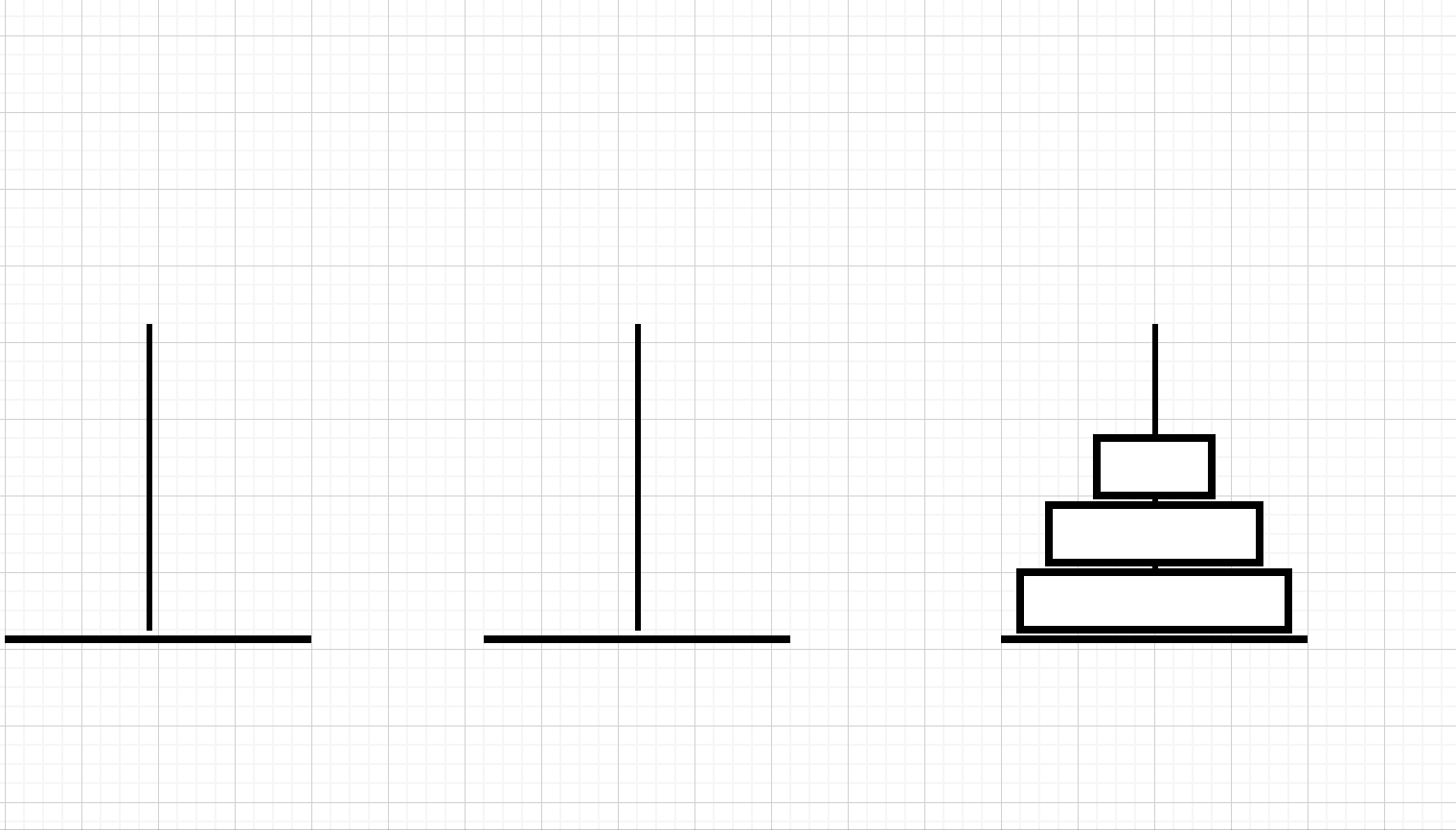
我不知道有没有朋友跟我一样有一个疑问,如果我们顶端的先放到中间柱子呢?

但是实际上汉诺塔问题解决方案都是最优解,我们不走弯路,我们的目的性非常强,我们最终目的都是移动到c,所以我们可以先让顶端的木块直接到c
解题思路:
不妨将这个问题拆解,n个汉诺塔,我们可以把最底下最大那个看成单独的一个,上面的(n - 1)个,看成一个整体.这样子最底下那个可以直接从 A 移动到 C,剩下上面的 ( n - 1 ) 个汉诺塔我们可以先从A 通过 C 移动到 B . 再从B通过 A 移动到 C.
这样子不断进行递归,问题规模就可以逐层减小.
代码:
def hanoi(n,a,b,c):#n为层数 a,b,c是杆子if n>0:#将中间 n - 1 个盘子当成一个整体,通过c盘从a移动到b盘hanoi(n-1,a,c,b) # 中间柱子变目标print("Moving from %s to %s" %(a,c)) # 对应一个柱子的时候hanoi(n-1,b,a,c) # 最后一个柱子变成目标hanoi(1,"A","B","C")运行结果:

青蛙跳台阶 

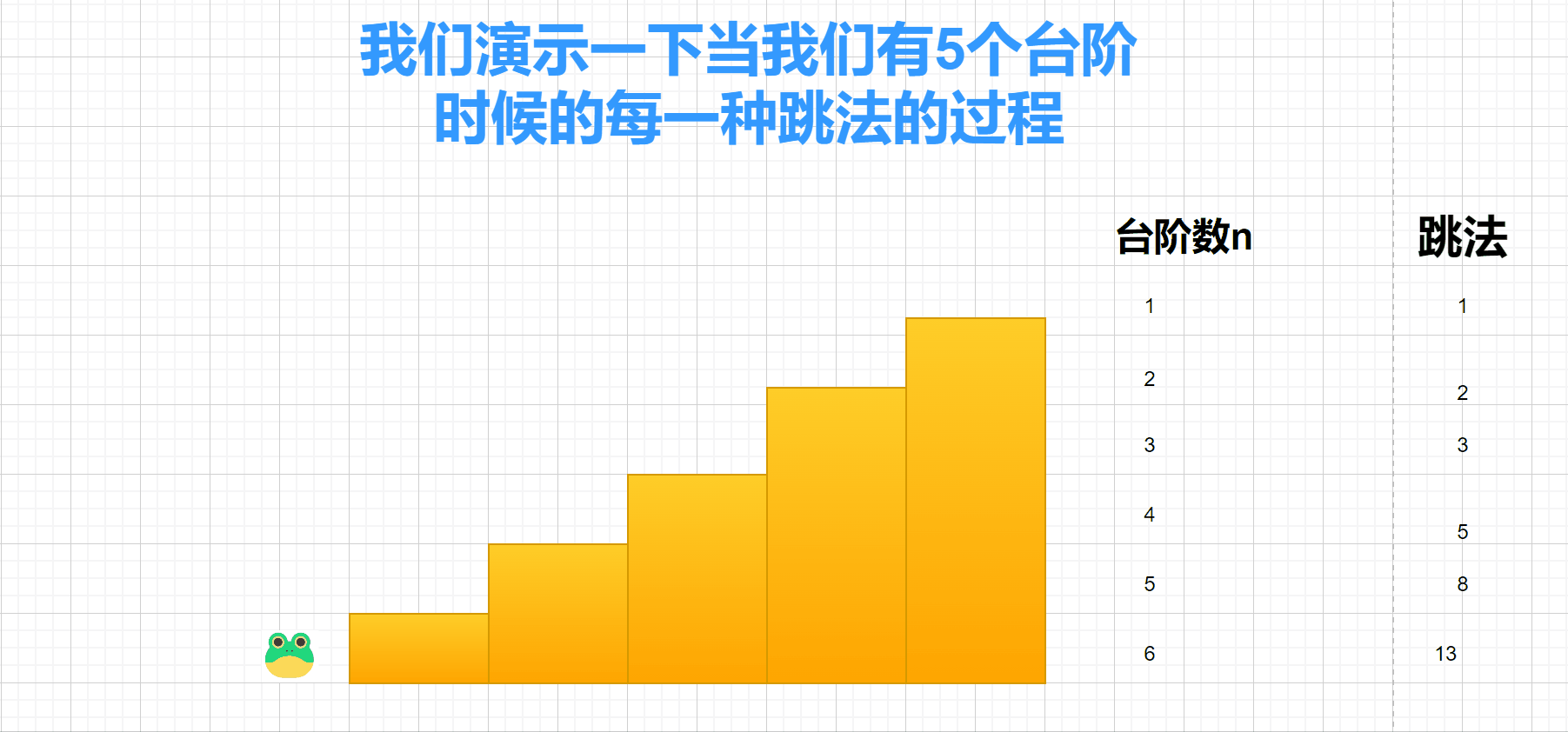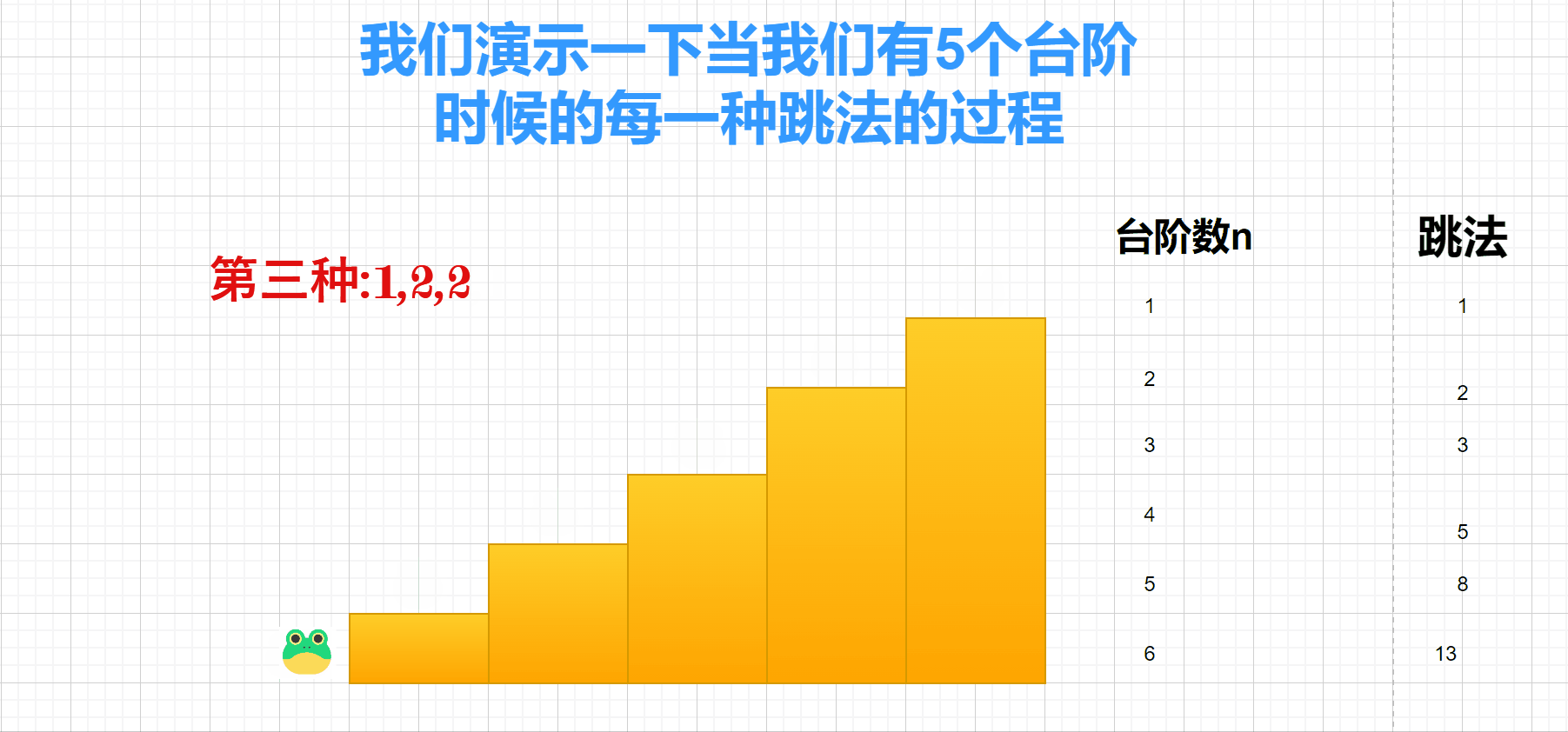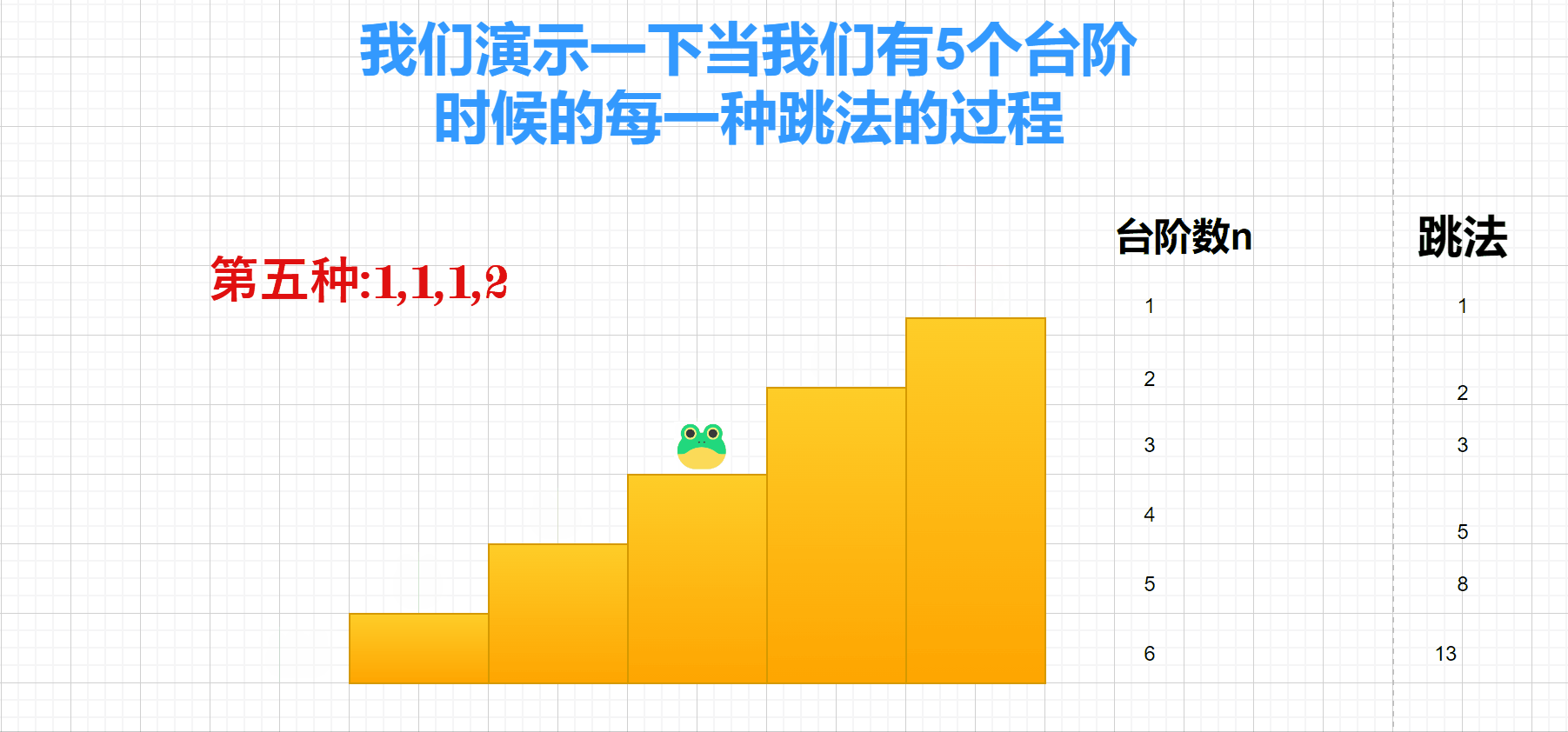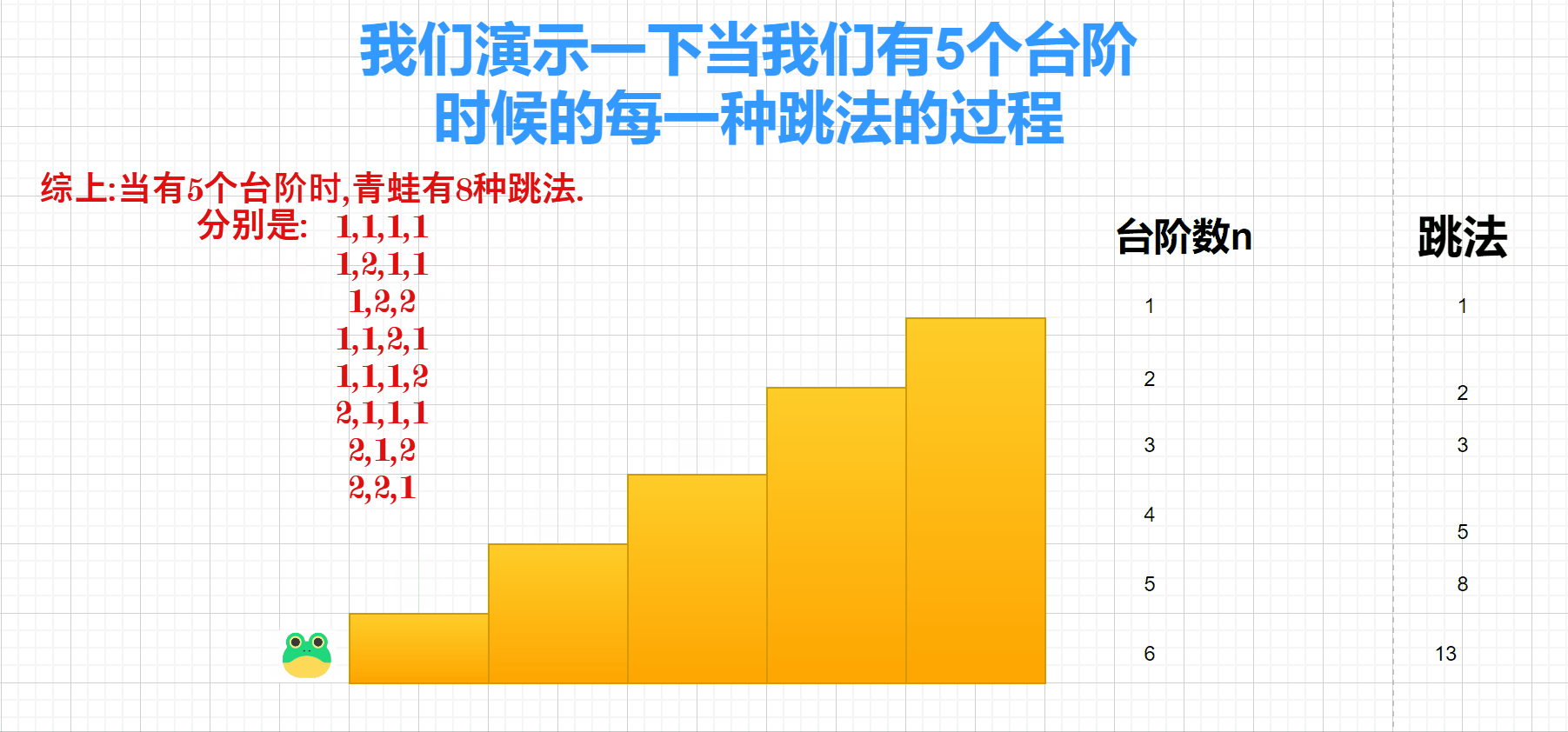
总结一下规律:
我们可以发现
跳 n 个台阶的台阶数对应的跳法 = 跳 (n - 1)个台阶时候的跳法 + 跳 (n - 2)个台阶时候的跳法.
这有点像我们的斐波那契数列.
青蛙跳台阶的问题相当于动态规划的问题 .
动态规划:用上一步的结果,来快速计算得到下一步的结果.
递归的思路:
当只有1个台阶时,只有一种跳法;当有2个台阶时,有两种跳法;当台阶数大于2时,青蛙可以选择跳一步到第n-1个台阶,也可以选择跳两步到第n-2个台阶,所以总的跳法数是跳到第n-1个台阶的跳法数加上跳到第n-2个台阶的跳法数。
这里是青蛙跳台阶的Python递归实现:
def frog_jump(n):if n == 1:return 1elif n == 2:return 2else:return frog_jump(n-1) + frog_jump(n-2)
其中,n表示台阶数,函数返回青蛙跳到第n个台阶的跳法数。
需要注意的是,这种递归实现虽然简单易懂,但是时间复杂度为指数级别的,所以不能用于大规模的数据处理。

这篇关于【Python数据结构与算法】--- 递归算法应用-五行代码速解汉诺塔问题.的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








