本文主要是介绍融合透镜成像反向学习的精英引导混沌萤火虫算法(Matlab),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
作者在前面的文章中介绍了萤火虫算法(FA),FA是一种功能强大、效率高的元启发式算法,该算法通过模拟自然界中萤火虫个体之间相互吸引的理想化行为达到寻优目的,在解决工程优化问题时表现出了良好的性能,一经提出便受到国内外研究人员的关注。
然而FA算法也存在一些缺陷:
首先,FA算法采用全吸引模型,由于FA算法中每只萤火虫都会被其他更亮的萤火虫吸引,吸引次数过多将导致收敛较慢,计算复杂度高;
同时,萤火虫算法的随机扰动步长α和吸引力步长β0是固定值,若取值较小,将使得算法过早成熟,陷入局部最优,若过大可能导致后期出现震荡或跳出最优解,因此该值应该根据不同阶段的需要动态调整;
最后,FA算法的吸引力随着个体之间的距离增加而减少,这意味这若两只萤火虫距离较远,较亮的萤火虫不会吸引较暗的萤火虫,整个种群将随着迭代自动细分为多个子种群,每个子种群都可能围绕着局部最优进行探索,这是个有效的策略,但当面临复杂优化问题时,往往存在许多局部最优,有些极值区域无法探索,这将导致算法陷入局部最优。
本文将针对FA算法的缺陷提出一种融合透镜成像反向学习的精英引导混沌萤火虫算法。
00 目录
1 萤火虫算法原理
2 融合透镜成像反向学习的精英引导混沌萤火虫算法
3 代码目录
4 算法性能
5 源码获取
01 萤火虫算法(FA)原理
卡卡在前面已经介绍过萤火虫算法原理及其MATLAB实现。
02 融合透镜成像反向学习的精英引导混沌萤火虫算法
针对在文首中提到的FA算法的种种缺陷,本文提出了以下改进。
2.1 改进的Circle混沌映射初始化
由前面的介绍可知,FA算法能够自动生成若干“子种群”,这在面临复杂优化问题时可能会陷入局部最优,但若如果初始值接近全局最优解,则算法将收敛很快。由于FA算法并无先验知识,故通常随机生成初始种群,此策略生成的种群分布不均匀,会导致种群多样性减少,种群质量不高,影响算法的收敛速度。
而混沌映射具有随机性、非重复性和混沌遍历性等特点[1],意味着它比依赖于概率的随机生成更能够使种群分布均匀。因此,可以利用混沌映射生成初始种群来增加潜在解的多样性。目前文献中常用的混沌映射有Logistic映射、Tent映射和Circle混沌映射等,而Circle映射较为稳定且其混沌值覆盖率高[2],但同时考虑到Circle映射在[0.2,0.6]之间取值较为密集,其分布并不均匀,因此对Circle映射公式进行改进[3],使其更加均匀。
原 Circle 混沌映射表达式为:
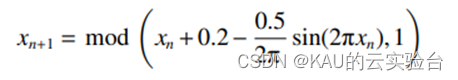
改进后的 Circle 混沌映射表达式为:

式中:n 为解的维度。
分别用Logistic映射、Tent映射、改进的Circle映射作出其分布图:
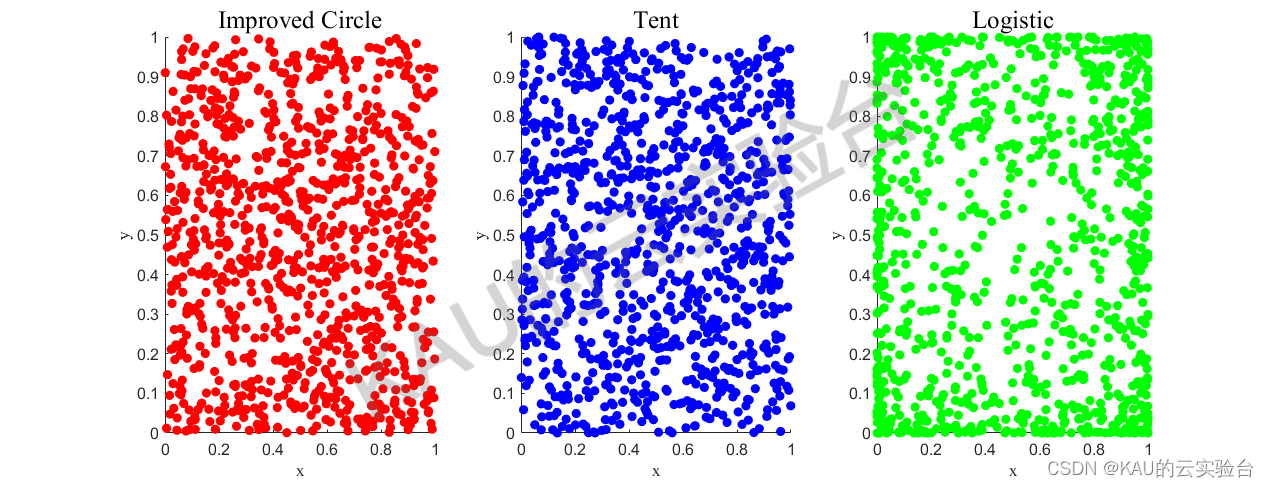
由结果可以看到,Logistic映射中间取值概率比较均匀,但在两端概率特别高,因此当全局最优点不在设计变量空间的两端时,对寻找最优点是不利的;其次Tent映射虽有较好的遍历性,但其迭代序列中存在小周期, 还存在不稳定周期点,因此若序列落入其中将导致序列趋于稳定,算法失效;最后,改进的Circle映射相对更加稳定且分布均匀性较好。
因此本文选用改进的Circle映射初始化FA算法的种群, 以提高和改善初始种群在搜索空间上的分布质量,加强其全局搜索能力。
2.2 精英引导策略
由前面的分析知,全吸引模型收敛速度慢,计算复杂度高,因此在这里提出一种精英吸引的策略,设定种群中适应度排序前1/4个体为精英个体,其余个体则属非精英群体。不同的群体将采用不同的更新策略。两个群体负责不同的任务,非精英群体受精英群体的领导探索,能够提高算法的勘探和开发效率,而精英群体进行就地搜索,负责局部的开发。
2.2.1 非精英群体
对于非精英群体,其仅受所有精英群体的吸引,更新策略将仍然采用FA算法中的策略。同时,考虑到若个体距离精英个体较远,其影响力将十分有限,因此这里重新定义吸引力β: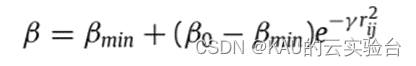
其中βmin为β的最小值,通过此改进,即使两个萤火虫相距很远,精英萤火虫仍能在一定程度上引导非精英萤火虫。
其次,通过观察原FA算法的位置更新公式可知,公式并没有显式的勘探或开发过程,本文通过引入一个惯性权重φ来解决:
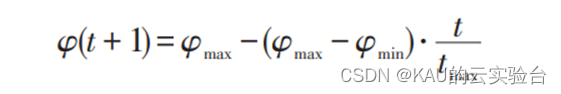
其中,φmax取0.9,φmin取0.4。通过引入惯性权重φ,在迭代初期,个体间距较大,此时惯性权重较大,算法能够在全局范围进行搜索,一定程度上提升算法的全局勘探能力;在迭代后期,个体间距大幅减小,此时惯性权重较小,算法能够进行局部开发。
改进后的非精英群体位置更新公式如下:
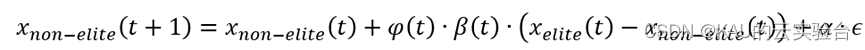
2.2.2 精英群体
精英群体由适应度最好的1/4个个体,储存了种群的优势信息。为保持这些优势信息不被丢失且还能寻得更有用的信息,让精英个体只在精英个体周围运动进行局部开发。
鲸鱼优化算法模拟了鲸鱼的层次结构和觅食行为,其螺旋泡网狩猎行为具有较好的局部寻优能力,因此本文引入鲸鱼优化算法的螺旋位置更新策略,充分利用精英群体中最优精英与其他精英之间的位置信息,而不是将精英们迅速靠近最优个体,既保证了算法的寻优能力又保证了种群的多样性。
精英群体位置更新公式如下:
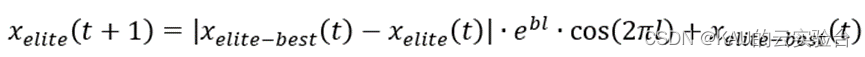
其中,xelite-best为精英群体中的最佳个体,xelite为当前的精英个体。
2.3 透镜成像反向学习策略
许多优化算法在面临复杂优化问题时常陷入局部最优,FA算法也不例外,其在迭代后期种群多样性降低,萤火虫群体聚集在最优个体附近,当最优个体陷入局部最优时难以跳出,导致算法早熟。因此本文采用透镜成像反向学习对最优萤火虫进行扰动,提高跳出局部最优的可能性。
反向学习是由Tizhoosh[7]提出的一种优化机制,其通过计算当前位置的反向解来扩大搜索范围,由此找到优化问题的更优解。将优化算法与反向学习相结合能够有效提升算法的寻优性能,但是反向学习存在一定的缺点,例如在迭代后期反向学习无法使算法有效跳出局部最优,导致算法收敛精度不足。基于此,透镜成像原理被引入其中,
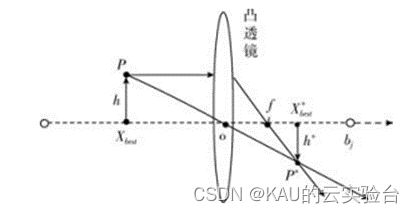
图源于[8]
假设某一空间中,全局最优位置Xbest是将一个高度为h 的个体P投影到x 轴上得到的,坐标轴的上下限为aj和bj 表示当前解第j维的上下限,在原点o上放一个焦距为f 的凸透镜,通过凸透镜成像可以得到一个高度为h* 的P* , 此时在x轴得到通过成像产生的最优位置X* best (反向点)。所以由透镜成像原理可以得出:
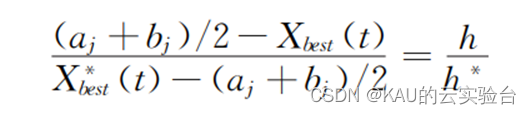
设h/h* =n,通过变换得到X* ,表达式如下:
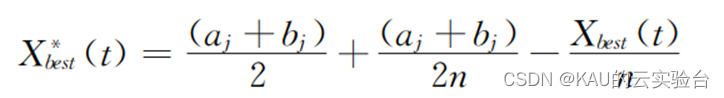
当n=1时,上式即为文献[7]中一般反向学习反向解的求解公式。显然,一般反向学习是透镜成像反向学习的一个特例。采用一般反向学习得到的反向解是固定的,而在透镜反向学习中通过调整 n的大小,可以获得动态变化的反向解,进一步提高算法寻优精度。同时,较小的n生成的反向解范围大,而较大的n产生小范围内的反向解,结合FA算法前期大范围搜索而迭代后期局部精细搜索的特点,引入动态变化的n:
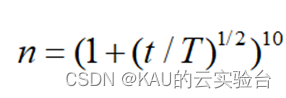
随着迭代次数增加,n值将变大,其反向解的范围将变小。同时考虑到产生的反向解不一定优于原解,引入贪婪策略,使得只有当反向解优于原解时才进行替换(这里也可以考虑用模拟退火的Metropolis接受准则)。
03 代码目录
考虑到很多同学获取代码后有乱码(matlab版本问题),可以将matlab版本改为2020以上,或使用乱码解决文件夹中的txt文件即可。
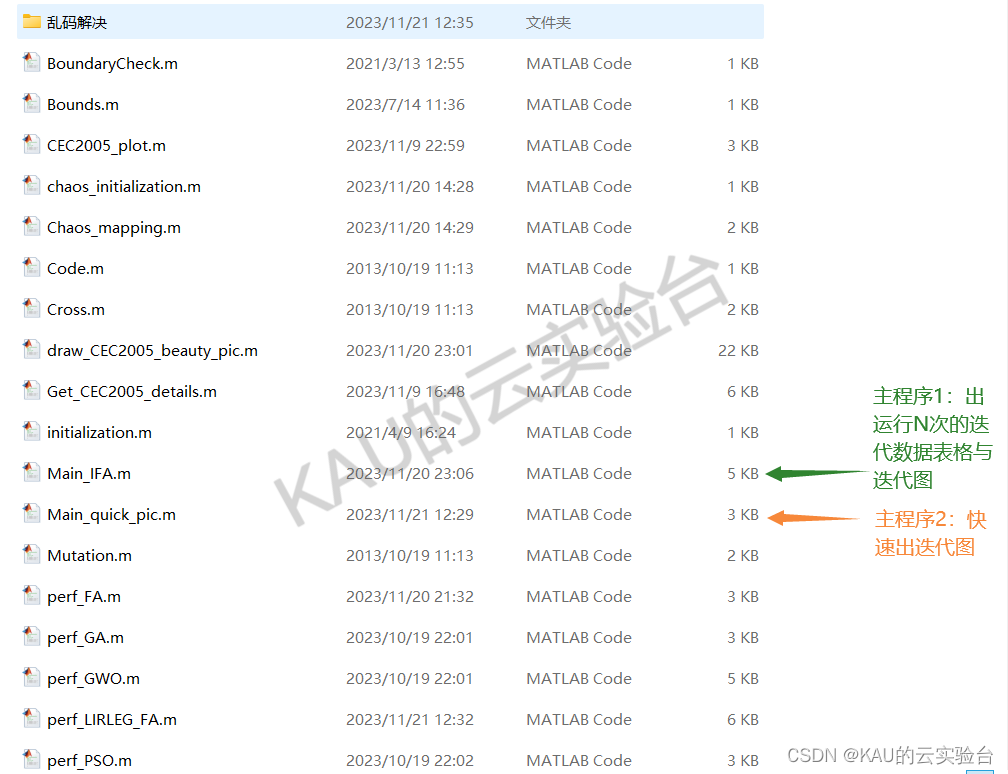
部分代码:
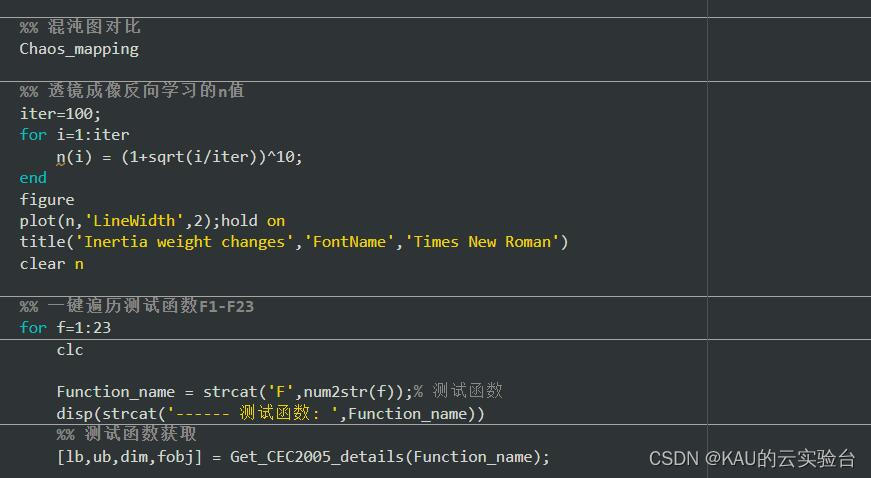
04 算法性能
采用05年的标准测试函数来检验其寻优性能,该测试集是应用最多、最经典的测试集,包含23个Benchmark函数,其中F1-F5为单峰函数,F6-F12为基本的多峰函数,F13-F14为扩展的多峰函数,F15-F23为多峰组合函数
其运行结果如下:

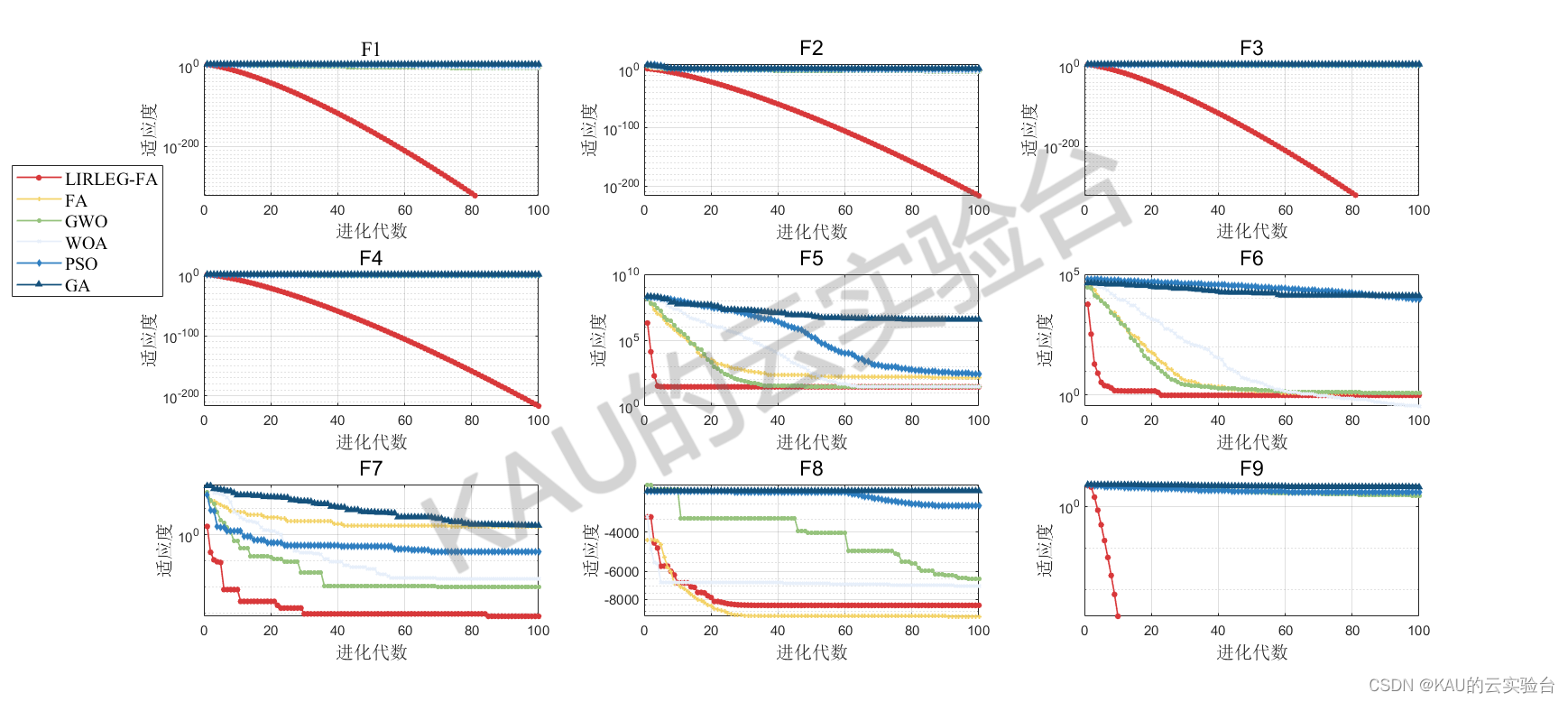
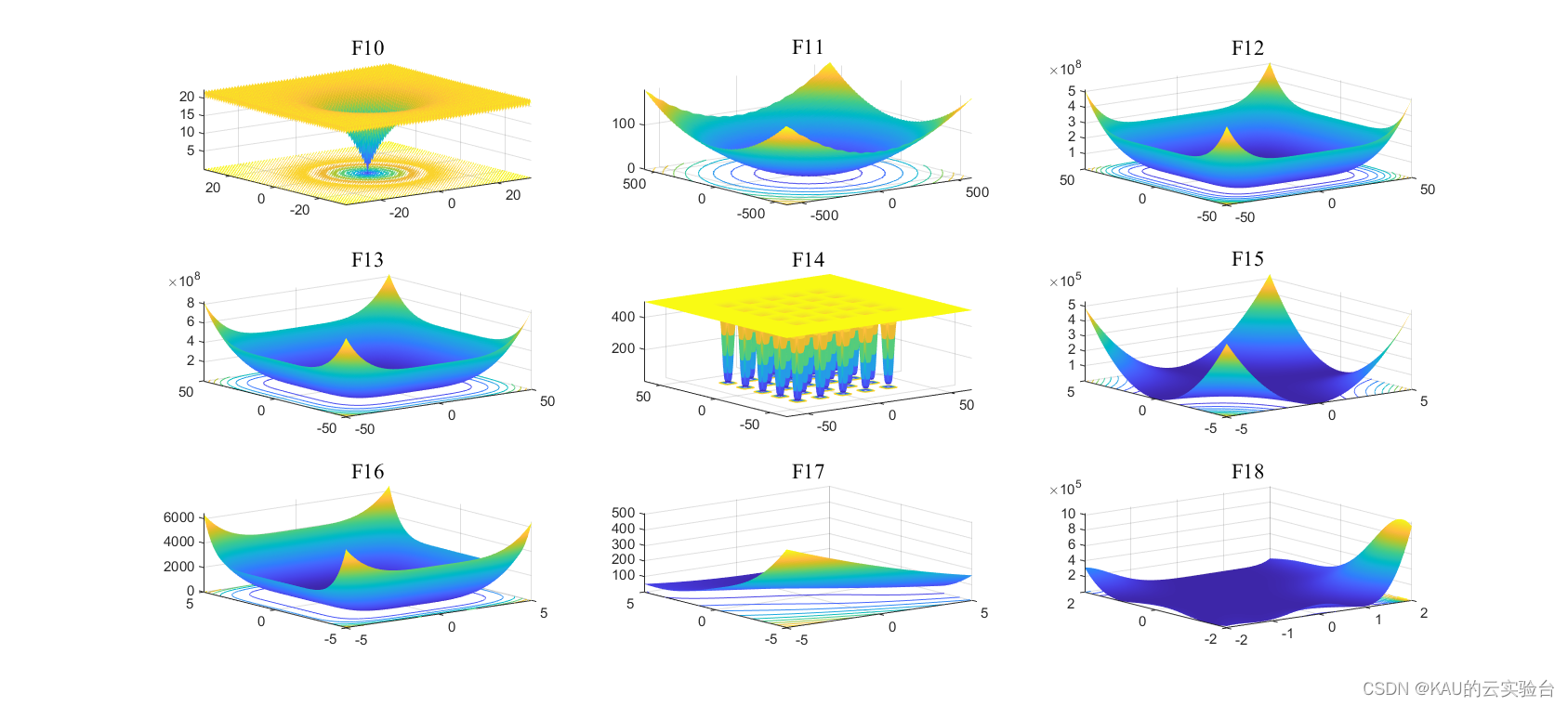

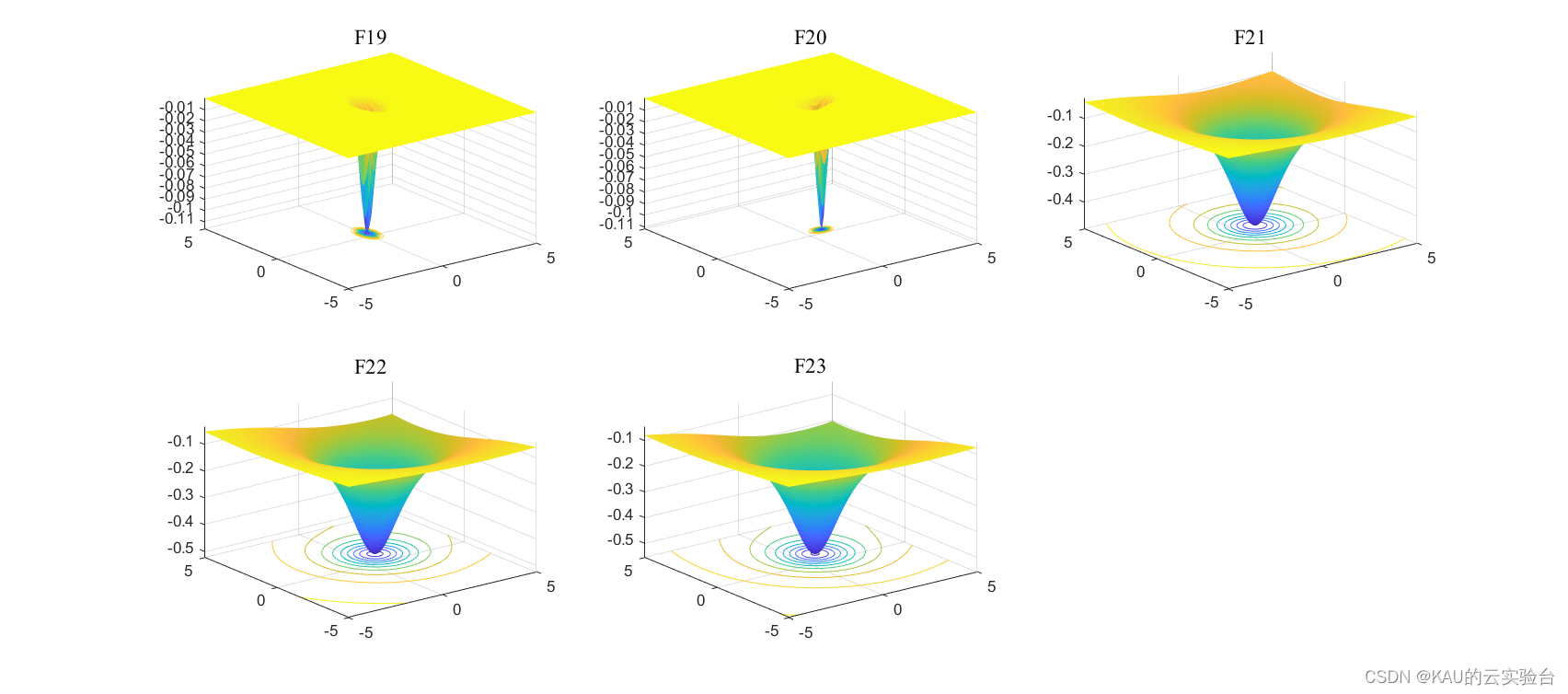
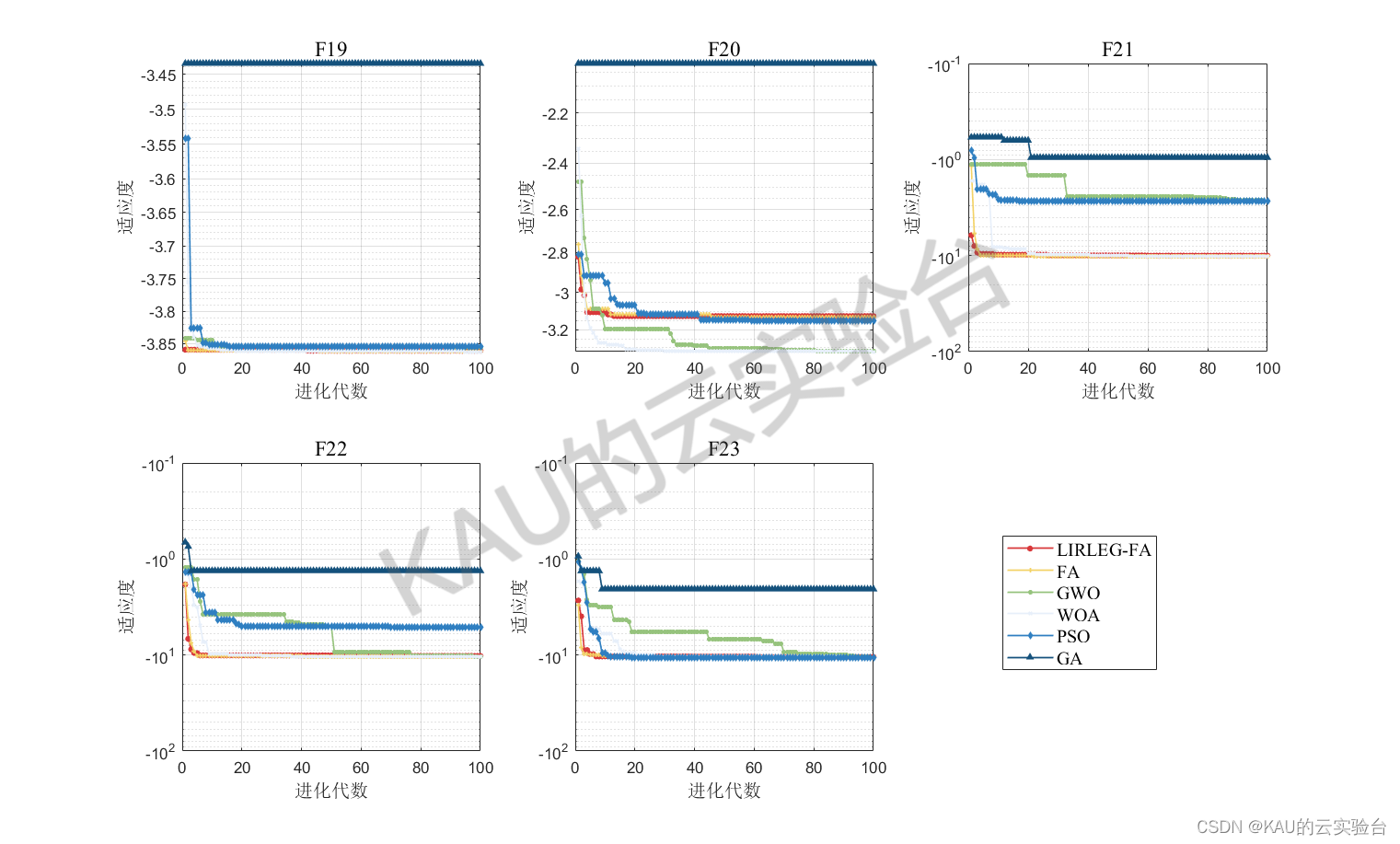
由结果可以看到,改进的萤火虫算法在多数函数的收敛速度和精度都更好,改进算法的效果良好。
05 源码获取
在GZH:KAU的云实验台
参考文献
[1] Shi X,Li M. Whale Optimization Algorithm Improved Effectiveness Analysis Based on Compound Chaos Optimization Strategy and Dynamic Optimization Parameters [ c ]//2019 International Conference on Virtual Reality and Intelligent Systems( ICVRIS) . 2019:123-126.
[2]ZHANGD M, XU H, WANG Y R, et al. Whale optimization algorithm for embedded Circle mapping and onedimensional oppositional learning based small hole imaging[J]. Control and Decision, 2021, 36(5): 1173-1180(in Chinese).
[3] 宋立钦,陈文杰,陈伟海等.基于混合策略的麻雀搜索算法改进及应用[J].北京航空航天大学学报,2023,49(8):2187-2199.
[4] 李德毅,孟海军,史雪梅.隶属云和隶属云发生器[J].计算机研究与发展,1995(6):15
[5] 李德毅,刘常昱.论正态云模型的普适性[J].中国工程科学,2004,6(8):28-34.
[6] 张 铸,饶盛华,张仕杰.基于自适应正态云模型的灰狼优化算法[J].控制与决策,2021,36(10):2562-2568.
[7] TIZHOOSH H R.Opposition-based reinforcement learning[J].Journal of Advanced Computational Intelligence and Intelligent Informatics, 2006,10( 4):578-585.
[8] 徐航,张达敏,王依柔等.混合策略改进鲸鱼优化算法[J].计算机工程与设计,2020,41(12):3397-3404.
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发,可以点击右下角的赞/在看(ง •̀_•́)ง(不点也行),你们的鼓励就是我坚持的动力!若有定制需求,可私信作者。
这篇关于融合透镜成像反向学习的精英引导混沌萤火虫算法(Matlab)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






