深入解析序列模型：全面阐释 RNN、LSTM 与 Seq2Seq 的秘密

探索序列建模的基础知识和应用。

简介

序列建模是许多领域的一个重要问题，包括自然语言处理 (NLP)、语音识别和语音合成、时间序列预测、音乐生成和「生物信息学」。所有这些任务的共同点是它们需要坚持。接下来的事情的预测是基于历史的。例如，在“哈桑以前踢足球，而且他踢得非常好”的序列中。只有将“哈桑”的信息推进到该特定点，才能对“他”进行预测。因此，您需要某种历史记录块来存储以前的信息并将其用于进一步的预测。传统的人工神经网络在这方面失败了，因为它们无法携带先前的信息。这就催生了一种名为“循环神经网络（RNN）”的新架构。

循环神经网络

循环神经网络是一种深度学习神经网络，它会记住输入序列，将其存储在记忆状态中，并预测未来的单词/句子。它们中有循环，允许信息持续存在。

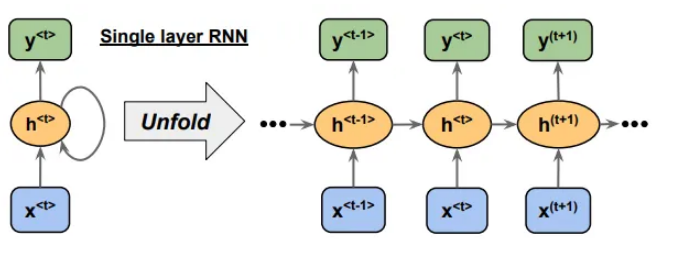
上面显示的单层 RNN 具有输入 x 和输出 y，以及隐藏单元 h。该图的右侧部分以展开的方式显示了 RNN。考虑隐藏单元h(t)的情况；它接收两个输入。一个是x(t)，另一个是h(t-1)。这样，信息就得以传承。

该 RNN 架构的修改版本可用于解决不同类型的序列问题。序列问题大致可分为以下几类：

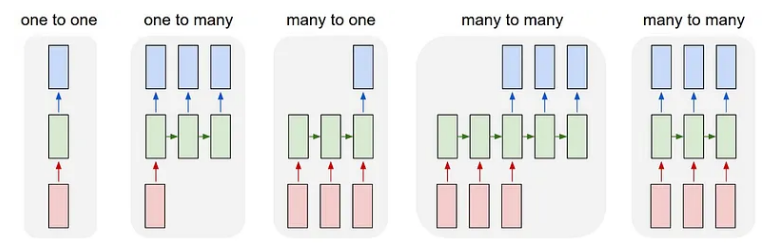
多对多架构可用于视频字幕和机器翻译。一对多用于图像字幕，多对一用于情感分析任务。这些只是这些修改后的架构的一些应用。

RNN 的缺点

1. 梯度消失/爆炸：总损失是所有时间戳损失的总和。因此，在反向传播过程中，我们对权重求偏导数。应用链式法则，最终给出了一种形式，我们可以在其中计算相邻时间戳处隐藏状态的偏导数的乘积。由于这种乘法，我们的梯度可以呈指数级减小，并且参数的更新相当小。这就是梯度消失问题。当梯度呈指数增长时，参数更新不稳定且不可预测。这就是梯度爆炸问题。这两个问题都阻碍了 RNN 的训练。
2. 长期依赖性：RNN 可以轻松地在小间隙中传递信息，但是当最后一个单词依赖于长句子的第一个单词时，RNN 会因间隙过大而失败。

为了克服上述问题，我们可以使用梯度裁剪、跳跃连接、权重初始化技术、梯度正则化和门控架构（如 LSTM 和 GRU）。

长短期记忆

LSTM 是一种深度学习神经网络，具有隐藏状态和细胞状态两种不同的状态。它具有三种不同类型的门，即输入门、遗忘门和输出门。这些门调节进出记忆单元的信息流，使 LSTM 能够根据需要选择性地记住或忘记信息。

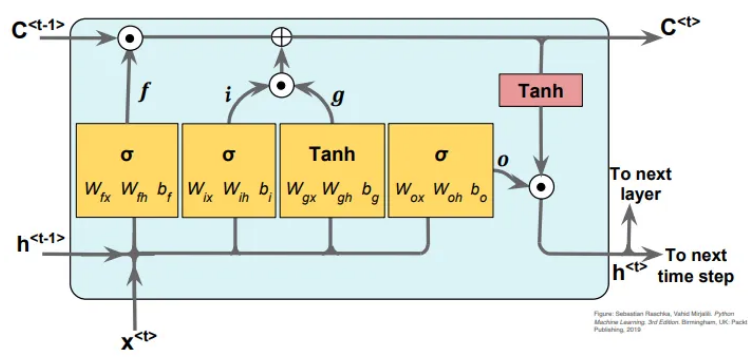
现在我将解释 LSTM 的工作原理。一个 LSTM 单元采用输入 x(t)、隐藏状态 h(t-1)、单元状态 c(t-1)。基于 h(t-1) 和 x(t)，它首先决定使用遗忘门丢弃哪些信息。然后我们决定哪些新信息应该存储在单元状态中。我们通过使用输入门和输入节点找到了这一点。然后我们通过首先忘记然后添加新信息来更新单元状态 c(t-1)。最后，我们使用更新的单元状态 c(t)、输入 x(t)、隐藏状态 h(t) 和输出门来计算输出。

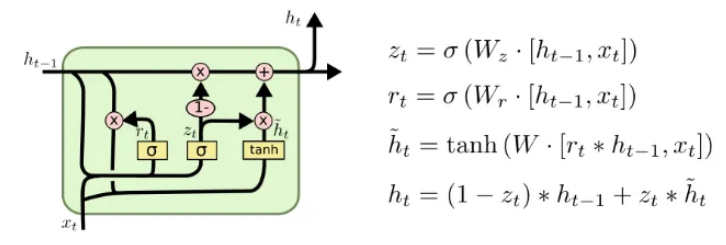
LSTM 面临过度拟合、内存限制和计算复杂性。建议对 LSTM 架构进行许多小的修改。一种架构是门控循环单元 (GRU)：

序列到序列

Seq2Seq 是一种特殊类型的序列建模，用于机器翻译、文本生成、摘要等。其架构的设计方式使其可以接受可变数量的输入并产生可变数量的输出。它有一个编码器和解码器。编码器和解码器都有一个循环神经网络。

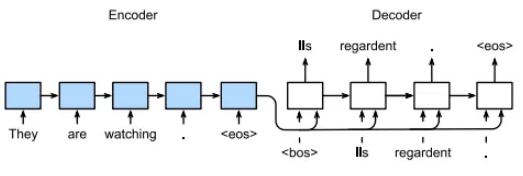
在上图中，您可以看到编码器在每个时间戳处获取一个输入标记，然后更新其隐藏状态。编码器从给定句子中捕获的所有信息都通过编码器的最后一个隐藏状态传递到解码器。最后一个隐藏状态称为上下文向量。它充当整个输入序列的摘要。解码器 RNN 获取编码器生成的上下文向量，并逐个生成输出序列令牌。在每个时间步，解码器接收先前的输出令牌（或初始时间步期间的开始令牌）及其隐藏状态。解码器的隐藏状态根据先前的隐藏状态和先前生成的令牌进行更新。解码器逐个生成输出序列标记，直到满足特定条件，例如达到最大长度或生成序列结束标记。

Seq2Seq的缺点

1. 上下文压缩：来自输入序列的所有信息必须压缩到上下文向量的大小。因此，损失细粒度的细节。
2. 短期记忆限制：他们努力从遥远的时间步骤捕获和保留信息，从而难以处理长序列和捕获长期依赖性。
3. 偏见：在培训期间，经常使用称为“teacher forcing”的技术对SEQ2SEQ模型进行训练，在该技术中，将解码器与地面真相输出tokens一起提供为每个时间步骤的输入。但是，在推理或测试期间，该模型根据其自身的预测生成输出tokens。训练和推理之间的这种差异可能导致暴露偏见，从而导致模型在推断期间表现出色。

总结

考虑到以上所有因素，循环神经网络确实在序列建模方面做出了很大的改变。为了克服它的缺点，我们提出了 LSTM 和 GRU。但最具革命性的变化是注意力机制的出现。