本文主要是介绍咸鱼游戏涂色游戏的逻辑分析与目标块执行步骤推演,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
咸鱼游戏中有许多小游戏,我在玩小游戏的时候发现了一个涂色小游戏。
下方地址是我的代码地址,可以查看完整代码,并进行测试。
GitHub - Basicconstruction/Painter: 涂色游戏的简单实现和算法解决
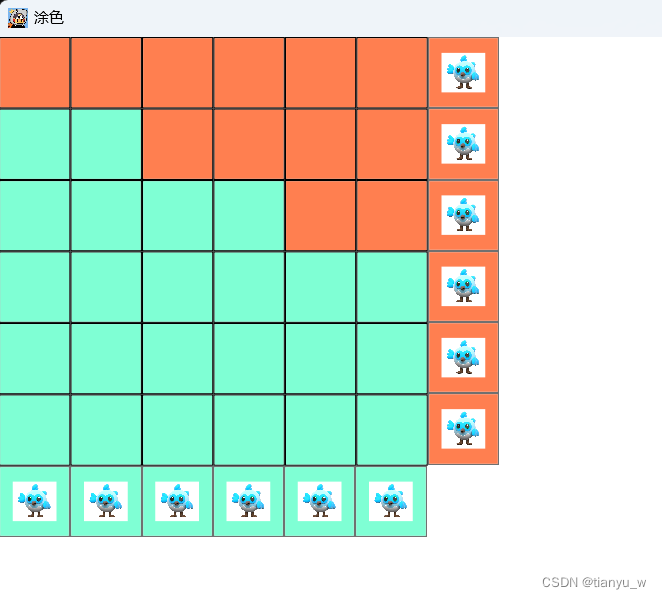
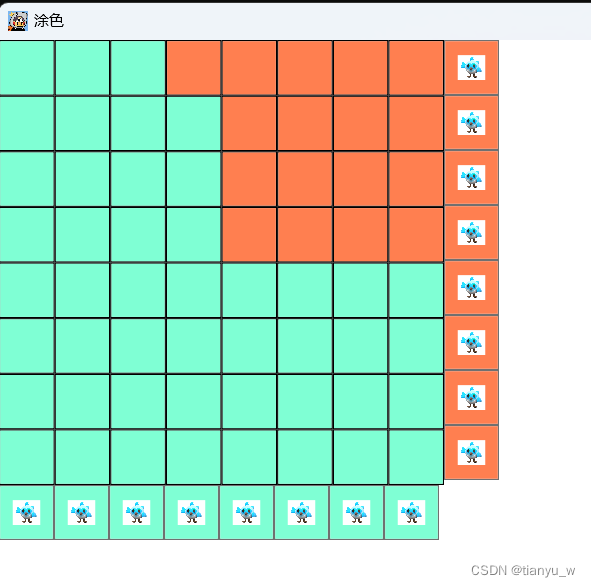
类似于下面的涂色,为了完成游戏,我们需要使用右侧和下侧的刷子吧方块刷到目标色。
下图是我实现的涂色游戏的逻辑,这两个图展示的分别是初始图,和目的图。
我们需要使用若干的右侧刷子和若干的下侧刷子,吧初始图刷成目标图。

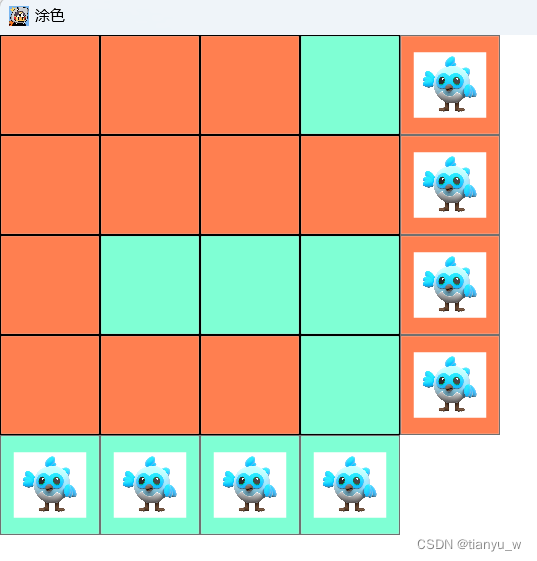
很显然,在玩的时候一些简单的多用眼睛观察,然后思考一下,就可以刷成,但是对于复杂的就比较难以完成。这个玩法比较有意思,于是在我们的网路应用编程的课大作业时,我把这个玩法推荐给了我们班的一个小组。
玩这个游戏的时候,我不禁思考,如何使用代码来计算出最短的刷子路径。我想着开发一个wcf的程序,放在抖音直播里面,让特定的直播观看者尝试或者让他和机器人来比较速度。
结果,抖音的Api不太容易获得。但是,我想这可以以其他形式来开直播,尽管我现在放弃了这个想法,这需要不少的精力,但是扑街的可能性还是比较大。
但是,在前天,我实现了n维的涂色游戏的游戏类,可以创建1*1,2*2,3*3,4*4,。。。20*20,等等的涂色游戏。当然如果你的显示屏够大也可以创建更多。
昨天我试着推演他的规律,尝试通过逆推解决,昨天思路没有打开,今天打开了思路,并解决了问题。
首先: 不是所有的目标都是可解的,对于2*2的,对角线就是不可解的,更高维度的也有不可解的。
在我的算法中,不可解的目标是,在寻找上一步的步骤时,找不到时判断是否已经解决,如果没有解决就是不可解的。
这个解决是思路的转变,是从Uncertain 到 Any的转变。
我先贴一下代码:
枚举类:
public enum Direction{Row,Col,}
public enum PaintType{One,Zero,Any,}数据结构和解决算法:
using System;
using System.Collections.Generic;
using System.Linq;namespace Reverse
{public class Cube{private readonly PaintType[,] _miss;private readonly int _axis;public Cube(int axis){_axis = axis;_miss = new PaintType[axis, axis];}public Cube(int axis, PaintType[,] miss){_axis = axis;_miss = miss;}public void Init(){for (var i = 0; i < _axis; i++){for (var j = 0; j < _axis; j++){_miss[i, j] = PaintType.Zero;}}}public static List<Result> Sort(List<Result> results){var tmp = new List<Result>();var res = new List<Result>();if (results.Count < 1){return null;}var direction = results.First().Direction;foreach (var ele in results){if (ele.Direction == direction){tmp.Add(ele);}else{res.AddRange(PartSort(tmp));tmp.Clear();direction = ele.Direction;tmp.Add(ele);}}if (tmp.Count > 0){res.AddRange(PartSort(tmp));}return res;}private static List<Result> PartSort(List<Result> results){results.Sort((r1, r2) => r1.Num.CompareTo(r2.Num));return results;}public void RandomMix(int count){var random = new Random((int)DateTimeOffset.Now.Ticks);var i = random.Next(_axis);var j = random.Next(_axis); _miss[i, j] = PaintType.One;Console.WriteLine($"Item {i} {j}");var start = new List<(int, int)> { (i,j) };while (count > 0){var list = new List<(int,int)>();var top = (i - 1, j);var bottom = (i + 1, j);var left = (i, j - 1);var right = (i, j + 1);if (Valid(top)&&NotResult(top)){list.Add(top);}if (Valid(bottom)&&NotResult(bottom)){list.Add(bottom);}if (Valid(left)&&NotResult(left)){list.Add(left);}if (Valid(right)&&NotResult(right)){list.Add(right);}if (list.Count != 0){var tuple = list[random.Next(list.Count)];_miss[tuple.Item1, tuple.Item2] = PaintType.One;count--;i = tuple.Item1;j = tuple.Item2;start.Add((tuple.Item1,tuple.Item2));Console.WriteLine($"Item {tuple.Item1} {tuple.Item2}");}else{Console.WriteLine("Back");var tuple = start.Last();start.Remove(tuple);i = tuple.Item1;j = tuple.Item2;}}}private bool NotResult((int, int) tuple){return _miss[tuple.Item1, tuple.Item2] != PaintType.One;}private bool Valid((int,int) tuple){return Valid(tuple.Item1) && Valid(tuple.Item2);}private bool Valid(int index){return index >= 0 && index < _axis;}public class Result{public Direction Direction{get;set;}public int Num{get;set;}public Result(){}public Result(Direction direction, int num){Direction = direction;Num = num;}public override string ToString(){return $"{Direction} {Num}";}}private bool Success(){for (var i = 0; i < _axis; i++){for (var j = 0; j < _axis; j++){if (_miss[i, j] != PaintType.Any) return false;}}return true;}private Result FindReverse(){// 查找行 onefor (var i = 0; i < _axis; i++)//行{var row = true;// 需要保持true,有一个false就可省略var notAllAny = false;for (var j = 0; j < _axis; j++)// 列{if (!row){break;}row = _miss[i, j] != PaintType.Zero;// one or anyvar tmp = _miss[i, j] != PaintType.Any;if (tmp){notAllAny = true;}}//Console.WriteLine($"row {row} notAllAny {notAllAny}");if (row&¬AllAny){return new Result(Direction.Row,i);}}// 查找列 zerofor (var j = 0; j < _axis; j++)// 列{var col = true;var notAllAny = false;for (var i = 0; i < _axis; i++)// 行{if (!col){break;}col = _miss[i,j] != PaintType.One;var tmp = _miss[i, j] != PaintType.Any;if (tmp){notAllAny = true;}}//Console.WriteLine($"col {col} notAllAny {notAllAny}");if (col&¬AllAny){return new Result(Direction.Col, j);}}return null;}private void Reverse(Result result){Reverse(result.Direction,result.Num);}private void Reverse(Direction direction, int num){if (direction == Direction.Row){for (var i = 0; i < _axis; i++)// 列{_miss[num,i] = PaintType.Any;}}else{for (var i = 0; i < _axis; i++)// 行{_miss[i,num] = PaintType.Any;}}}public void Print(){for (var i = 0; i < _axis; i++){for (var j = 0; j < _axis; j++){switch (_miss[i, j]){case PaintType.Any:Console.Write("A ");break;case PaintType.One:Console.Write("1 ");break;case PaintType.Zero:Console.Write("0 ");break;default:throw new ArgumentOutOfRangeException();}}Console.WriteLine();}}public static List<Result> PureSolve(Cube cube){if(cube==null) return null;var result = new List<Result>();var res = cube.FindReverse();while (res != null){result.Add(res);cube.Reverse(res);//cube.Print();res = cube.FindReverse();}if (cube.Success()){Console.WriteLine("算法求解成功!!");}else{Console.WriteLine("算法求解失败!!初始状态");cube.Print();}if (result.Count <= 1){return null;}while (result.Count>0&&result.Last().Direction==Direction.Col){result.Remove(result.Last());}result.Reverse();result = Sort(result);return result;}public static void Solve(Cube cube){if(cube==null) return;var res = cube.FindReverse();while (res != null){Console.WriteLine("找到可倒退的一行或一列(行: 一行不全是Any,且全部不是Zero; 列" +"一行不全是Any,且全部不是One)。");cube.Reverse(res);Console.WriteLine($"上一步的操作是 {res.Direction} {res.Num}.上一步是: ");//cube.Print();res = cube.FindReverse();}if (cube.Success()){Console.WriteLine("算法求解成功!!");}else{Console.WriteLine("算法求解失败!!初始状态");cube.Print();}Console.WriteLine("算法完成!");}}
}调用示例:
测试用例1,4维游戏,随机通过4邻域填充算法进行填充6个色块(提高有解的概率),
获得解决方案列表,输出结果
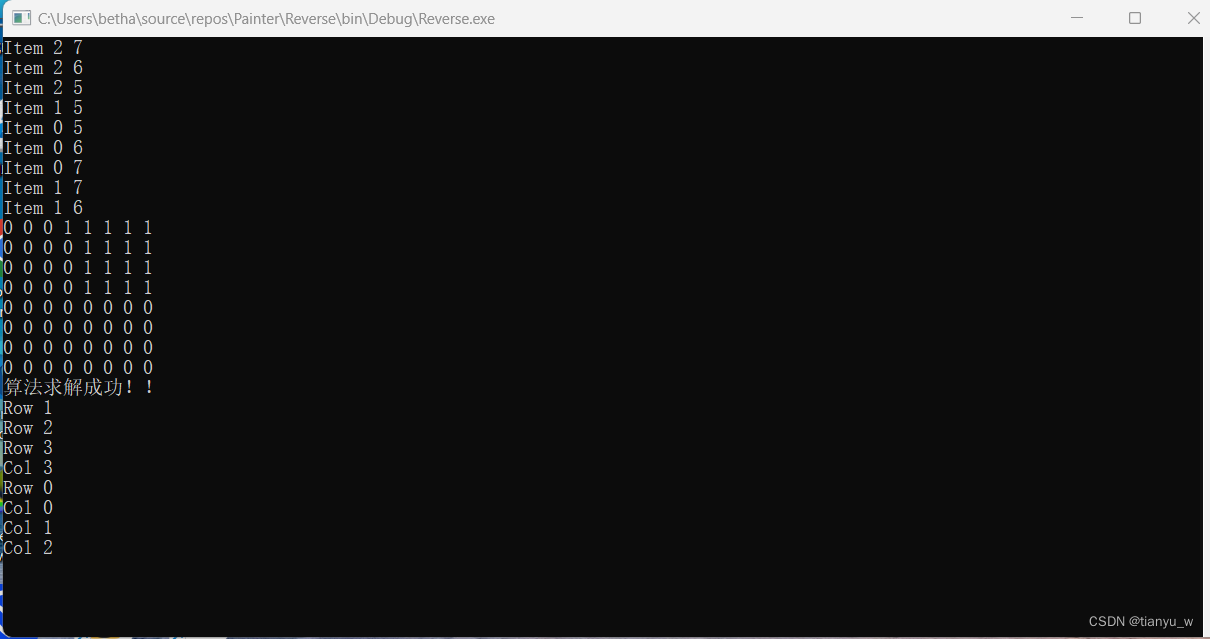
const int testNum = 1;var i = 0;while (i<testNum){var cube = new Cube(4);cube.Init();cube.RandomMix(6);cube.Print();var ps = Cube.PureSolve(cube);if (ps != null){foreach (var result in ps){Console.WriteLine(result);}}i++;}输出结果:
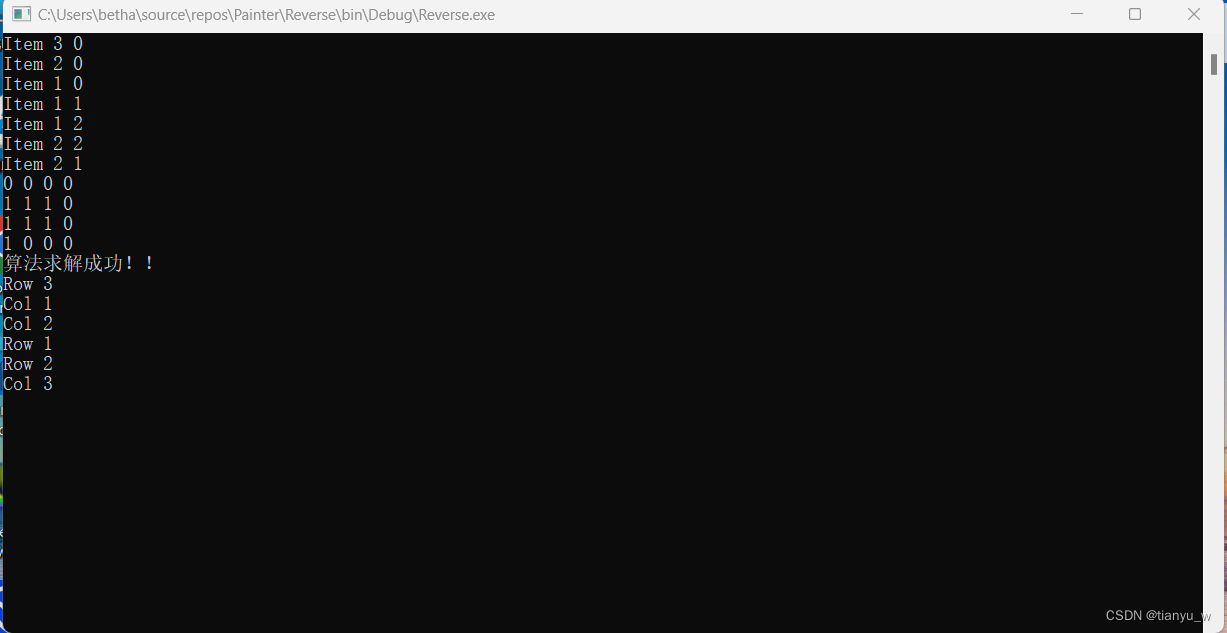
下面再进行简单解释:
对于一个待解目标,我们持续后推,直到所有的行和列都是Any。 推出所有的行和列都是Any说明有解,否则说明无解,无解的明显规律是,发现对于所有行和列,除了都是Any的,改行一定包含 Zero,列一定包含One。
如下面图示:
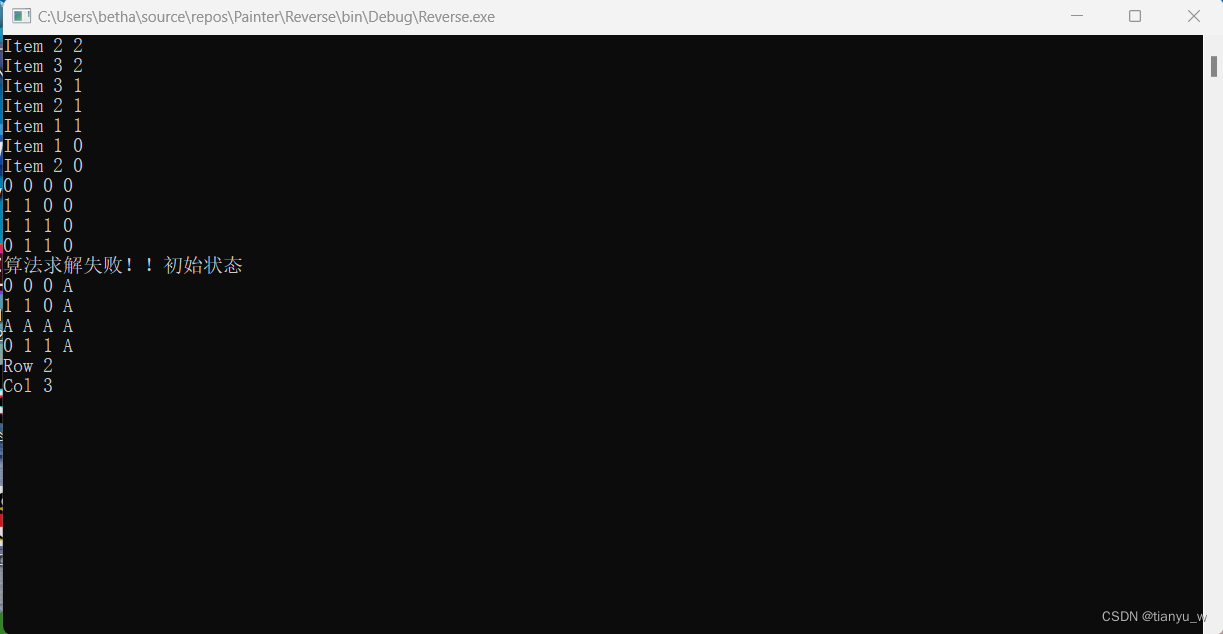
(One代表目标色,在右侧,Zero代表初始色,在下方,Any代表任意)
下方是 Solve的方法:
public static List<Result> PureSolve(Cube cube){if(cube==null) return null;var result = new List<Result>();var res = cube.FindReverse();while (res != null){result.Add(res);cube.Reverse(res);//cube.Print();res = cube.FindReverse();}if (cube.Success()){Console.WriteLine("算法求解成功!!");}else{Console.WriteLine("算法求解失败!!初始状态");cube.Print();}if (result.Count <= 1){return null;}while (result.Count>0&&result.Last().Direction==Direction.Col){result.Remove(result.Last());}result.Reverse();result = Sort(result);return result;}首先先判断,是否需要Solve,然后持续的进行倒推。直到不能进行倒推,然后判断是否解决。
最后是休整工作。
主要的流程是: 删除最终的几个 0(Col) 操作,如果有的话,这几个0操作的目的是把,包含0的一列转为全部为Any。 对于初始为全0的初始状态是不需要的。
然后进行部分排序。排序规则类似于把
A3 A2 A1 B4 A3 B5 B2 A0 A2
排序为
A1 A2 A3 B4 A3 B2 B5 A0 A2.
对于相邻的同属于行或列的几个操作进行按照序号从小到大排序,这样方便进行验证和观察。
下面是关键的寻找逆向操作的算法:
private Result FindReverse(){// 查找行 onefor (var i = 0; i < _axis; i++)//行{var row = true;// 需要保持true,有一个false就可省略var notAllAny = false;for (var j = 0; j < _axis; j++)// 列{if (!row){break;}row = _miss[i, j] != PaintType.Zero;// one or anyvar tmp = _miss[i, j] != PaintType.Any;if (tmp){notAllAny = true;}}//Console.WriteLine($"row {row} notAllAny {notAllAny}");if (row&¬AllAny){return new Result(Direction.Row,i);}}// 查找列 zerofor (var j = 0; j < _axis; j++)// 列{var col = true;var notAllAny = false;for (var i = 0; i < _axis; i++)// 行{if (!col){break;}col = _miss[i,j] != PaintType.One;var tmp = _miss[i, j] != PaintType.Any;if (tmp){notAllAny = true;}}//Console.WriteLine($"col {col} notAllAny {notAllAny}");if (col&¬AllAny){return new Result(Direction.Col, j);}}return null;}思路就是查找那一步可能是 上一步操作,需要满足,这一行只能包含 One或Any,但是也不能全是Any,因为全是Any的话就没有必要进行这一步操作。
这一列只能包含Zero或Any,但是也不能全是Any,理由同上。
解决方案的Painter2项目是可创建n*n涂色游戏的项目,可以算出的解决思路进行验证,不过需要修改代码,来适应更多的需求。

Reverse就是解决一个随机的涂色游戏的项目,不过对于特定的涂色目标,你需要手动编码,然后计算解决思路。
示例:
6维11个随机色块:
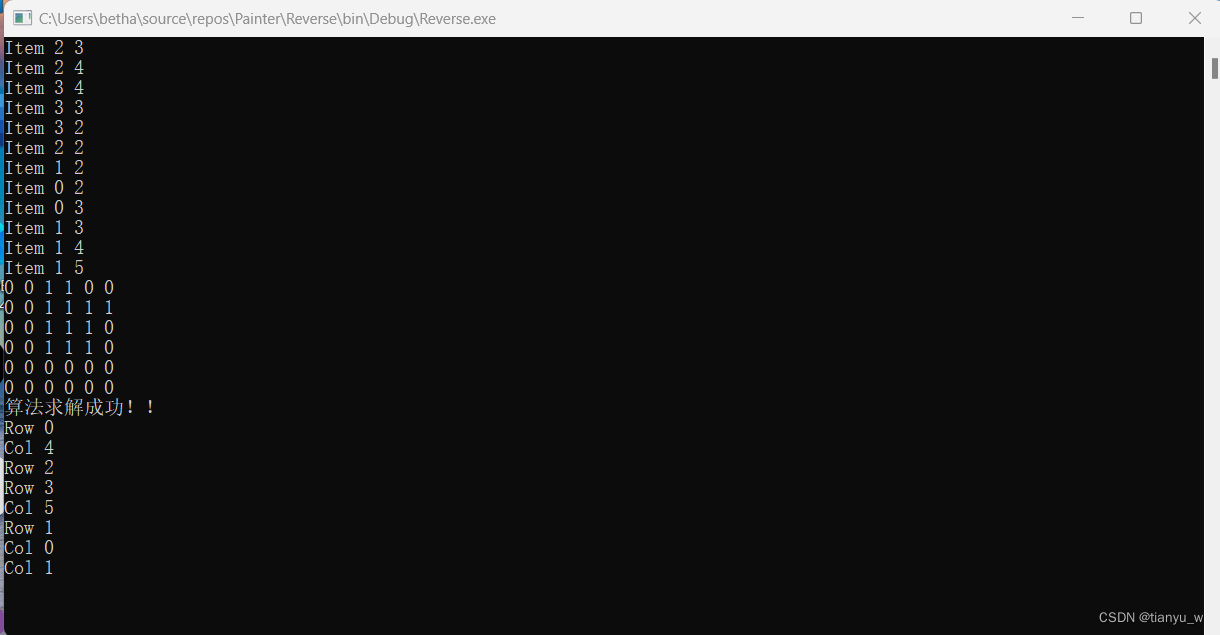

解决失败(无法逆推)

8维16个随机色块
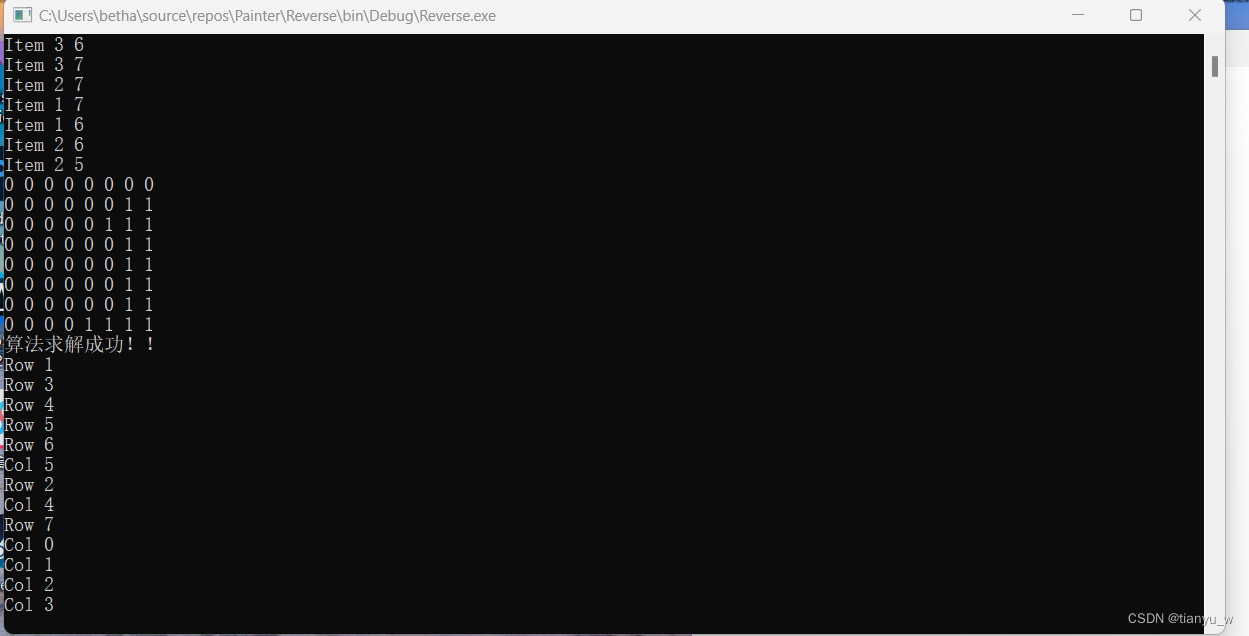
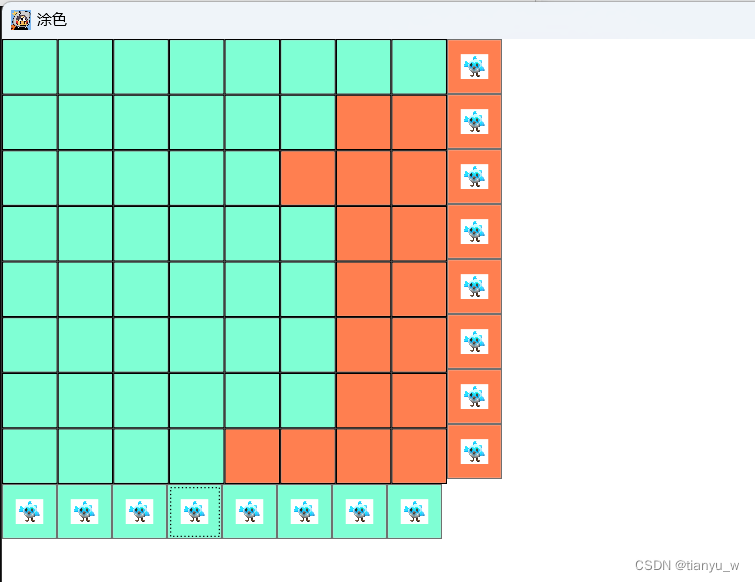
这篇关于咸鱼游戏涂色游戏的逻辑分析与目标块执行步骤推演的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


