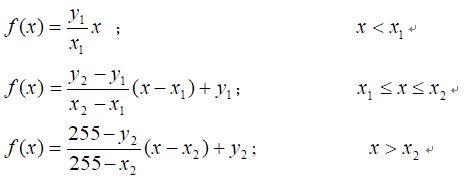基于分水岭算法的血管内膜中层厚度测量（一）

        最近看到一篇硕士论文中所研究的内容，在算法上我想想用opencv来实现，故意记录一下。论文名称《基于彩色超声图像的血管内膜中层厚度测量算法的研究》，下面所述的内容部分都是摘要其中的内容。

                                                                             图1 血管内膜中层原图

                                                                                图2 整个算法思路

1、灰度拉伸 

1）灰度直方图

直方图一般的定义都是灰度直方图（针对与灰度图像），opencv2中可以绘制灰度直方图的函数：calcHist（）；这有着很多重载函数，最常用的一种形式： 

C++: void calcHist(const Mat* images, int nimages, const int* channels, InputArray mask, OutputArray hist, int dims, const int* histSize, const float** ranges, bool uniform=true, bool accumulate=false )

参数详解：

onst Mat* images：输入图像

 int nimages：输入图像的个数

const int* channels：需要统计直方图的第几通道

InputArray mask：掩膜，，计算掩膜内的直方图  ...Mat()

OutputArray hist:输出的直方图数组

int dims：需要统计直方图通道的个数

const int* histSize：指的是直方图分成多少个区间，就是 bin的个数

const float** ranges： 统计像素值得区间

bool uniform=true::是否对得到的直方图数组进行归一化处理

bool accumulate=false：在多个图像时，是否累计计算像素值得个数
引用文章地址：https://blog.csdn.net/shuiyixin/article/details/80032167。

当然我们也可以根据Mat类写一个自己函数统计如下：

void Hist(cv::Mat &image){int table[256] = { 0 };int nr = image.rows;int nc =image.cols*image.channels();for(int j =0;j<nr;j++){uchar * data =image.ptr<uchar>(j);for(int i=0;i<nc;i++){table [data[i] ]++;}}double max = 0;int sum = 0;for (int i = 0; i < 256; i++) {sum += table[i];if (table[i] > max)max = table[i];//找到最大频次出现的数}Mat histgram(256, 256, CV_8U, Scalar(255));for (int i =0; i <=255; i++){line(histgram, Point(i, 255), Point(i, (255 - table[i]*255/max)), Scalar(0));}imshow("灰度直方图", histgram);
}

           
2）灰度均衡（直方图均衡）

在1）的情况下，开始用均衡的手法。我的理解所谓灰度均衡：是为了转换后的直方图是平的，满足每一个灰度级上有相同像素点的输出图像，但是实际过程中不会出现类似一条平的直方图，因为像素点最多只有256，太少。经过一些列的计算公式

void HistB(cv::Mat &image){int table[256] = { 0 };int nr = image.rows;int nc =image.cols*image.channels();for(int j =0;j<nr;j++){uchar * data =image.ptr<uchar>(j);for(int i=0;i<nc;i++){table [data[i] ]++;}}unsigned char bmap[256];for (int i = 0; i < 256; i++) {long temp = 0;for (int j =0;j<= i;j++){temp+=table[j];}bmap[i] =(unsigned char)(temp*255/image.rows/image.cols);//均衡化，这个公式是经过计算推导得来的}for(int j =0;j<nr;j++){uchar * data =image.ptr<uchar>(j);for(int i=0;i<nc;i++){data[i] = bmap[ data[i]];}}imshow("均衡直方图", image);
}

1）灰度拉伸

灰度拉伸和也属于灰度的线性变换，灰度拉伸和灰度线性变换相似。不同之处在于它是分段线性变换。表达式如下：

其中，x1和x2是分段函数的转折点。这里的转折点，从直方图上看就是从左边以及从右边看两个转折点（也就是增到减，或者减到增那个点）这里我们选择（20，550），（200，70）

void HistD(cv::Mat &image){int table[256] = { 0 };int nr = image.rows;int nc =image.cols*image.channels();int x1 = 30, y1 = 550, x2 = 200, y2 = 70;for(int j =0;j<nr;j++){uchar * data =image.ptr<uchar>(j);for(int i=0;i<nc;i++){if (data[i]<x1){data[i]  = y1/x1 *data[i];}else if (data[i]<x2 ){data[i] = (y2-y1)/(x2-x1)*(data[i] -x1)+y1;}else{data[i] = (255-y2)/(255-x2)*(data[i] -x2)+y2;}}}imshow("灰度拉伸之后图片", image);
}

这个和论文中的有出入，我对于灰度拉伸的理解是着两个转折点横坐标的范围转换为纵坐标饿范围，在直方图上可以很清楚的看见变化，但是从实际效果来说的话可能处理图像达不到预期的效果，这里还有待研究。

2、边缘检测 

       经典的边缘检测是以原始图像为基础，对图像的各个像素考察它的某个区域内灰度阶跃变化，利用边缘邻近的一阶或二阶方向导数变化规律做检测边缘。常用的边缘检测方法有：差分边缘检测、梯度边缘检测、Roberts 边缘检测算子、Prewitt 边缘检测算子、Sobel 边缘检测算子、Laplace 边缘检测算子等。在opencv中这些函数都是自带的:

Canny算子–Canny函数
消除噪声：使用高斯平滑滤波器卷积降噪。
计算梯度幅值和方向：此处按照sobel滤波器的步骤来操作：（1）运用一对卷积阵列（分别作用于x和y方向），（2）计算梯度幅值和方向，梯度方向一般取0度、45度、90度、135度这4个可能的角度之一。
非极大值抑制：这一步排除非边缘像素，仅仅保留了一些细线条（候选边缘）
滞后阈值：滞后阈值需要两个阈值（高阈值和低阈值） 
（1）若某一像素位置的幅值超过高阈值，该像素被保留为边缘像素。 
（2）若某一像素位置的幅值小于低阈值，该像素被排除。 
（3）若某一像素位置的幅值在两个阈值之间，该像素仅仅在连接到一个高于高阈值的像素时被保留。 
void Canny(inputArray,outputArray,double threshold1,double threshold2,int apertureSize=3,bool L2gradient=false) 
*第一个参数，输入图像，且需为单通道8位图像。 
*第二个参数，输出的边缘图。 
*第三个参数，第一个滞后性阈值。用于边缘连接。 
*第四个参数，第二个滞后性阈值。用于控制强边缘的初始段，高低阈值比在2:1到3:1之间。 
*第五个参数，表明应用sobel算子的孔径大小，默认值为3。 
*第六个参数，bool类型L2gradient，一个计算图像梯度幅值的标识，默认值false。
Sobel算子–Sobel函数
void Sobel(inputArray,outputArray,int ddepth,int dx,int dy,int ksize=3,double scale=1,double delta=0,int borderType=BORDER_DEFAULT) 
*第一个参数，输入图像。 
*第二个参数，输出图像。 
*第三个参数，输出图像深度。 
*第四个参数，x方向上的差分阶数。 
*第五个参数，y方向上的差分阶数。 
*第六个参数，Sobel核的大小，默认值为3，必须为1、3、5、7。当为1时，往往使用3x1、1x3的内核，这种情况下，没有进行高斯平滑操作。 
*第七个参数，计算导数值时可选的缩放因子，默认值1，表示默认情况下没用应用缩放。 
*第八个参数，表示在结果存入输出图像之前可选的delta值，默认值0。 
*第九个参数，边界模式。 
补充说明： 
（1）当内核大小为3时，Sobel内核可能产生比较明显的误差，为了解决这一问题，Opencv提供了Scharr函数，但该函数仅作用于大小为3的内核，该函数的运算与Sobel函数一样快，但结果却更加精确。 
（2）因为Sobel算子结合了高斯平滑和分化，因此结果会具有更多的抗噪性。

Laplacian算子–Laplacian函数
Laplacian算子是n维欧几里德空间中的一个二阶微分算子，定义为梯度grad的散度div。由于Laplacian使用了图像梯度，它内部的代码其实是调用了Sobel算子的。让一幅图像减去它的Laplacian算子可以增强对比度！！！ 
void Laplacian(inputArray,outputArray,int ddepth,int ksize=1,double scale=1,double delta=0,int borderType=BORDER_DEFAULT) 
*第一个参数，输入图像，且需为单通道8位图像。 
*第二个参数，输出的边缘图。 
*第三个参数，输出图像的图像深度。 
*第四个参数，用于计算二阶导数的滤波器的孔径尺寸大小，大小必须为正奇数，默认值为1。 
*第五个参数，计算拉普拉斯值的时候可选的比例因子，默认值为1。 
*第六个参数，表示在结果存入目标图之前可选的delta值，默认值为0。 
*第七个参数，边界模式。

Scharr滤波器–Scharr函数
在Opencv中主要是配合Sobel算子的运算而存在的。使用Scharr滤波器运算符计算x或y方向的图像差分。其实它的参数变量和Sobel基本上是一样的，除了没有ksize核的大小。 
void Scharr(inputArray,outputArray,int ddepth,int dx,int dy,double scale=1,double delta=0,int borderType=BORDER_DEFAULT) 
*第一个参数，输入图像。 
*第二个参数，输出图像。 
*第三个参数，输出图像深度。 
*第四个参数，x方向上的差分阶数。 
*第五个参数，y方向上的差分阶数。 
*第六个参数，计算导数值时可选的缩放因子，默认值1，表示默认情况下没用应用缩放。 
*第七个参数，表示在结果存入输出图像之前可选的delta值，默认值0。 
*第八个参数，边界模式。

参考文章地址：https://blog.csdn.net/qq_31531635/article/details/73382603 。

Mat src = imread("C:/Users/Administrator/Desktop/4.jpg");imshow("原始图片",src);Mat  dst0,dst1,dst11,dst2,dst22,dst3,dst33;//高斯滤波消除噪声// GaussianBlur(src, src, Size(3, 3), 0, 0, BORDER_DEFAULT);//转换为灰度图cvtColor(src, dst0, COLOR_RGB2GRAY);//HistD(dst0);//使用Laplace函数//第三个参数：目标图像深度；第四个参数：滤波器孔径尺寸；第五个参数：比例因子；第六个参数：表示结果存入目标图Laplacian(dst0, dst1, dst0.depth(), 3, 1, 0, BORDER_DEFAULT);//计算绝对值，并将结果转为8位convertScaleAbs(dst1, dst11);imshow("laplace效果图", dst11);Canny(dst0,dst2,3,9,3);convertScaleAbs(dst2, dst22);imshow("Canny效果图", dst22);Sobel(dst0,dst3,dst0.depth(),0, 1,3, 1, 1, BORDER_DEFAULT);convertScaleAbs(dst3, dst33);imshow("sobel效果图", dst33);

一般我们使用sobel算子进行滤波，很多算子存在在研究中 在实际应用中由于性能问题被淘汰。

3.分水岭分割算法

        分水岭分割方法（可以参考这一篇：https://blog.csdn.net/m0_37914500/article/details/80775454），是一种基于拓扑理论的数学形态学的分割方法，该方法的基本思想是把图像看作是测地学上的拓扑地貌，图像中每一点像素的灰度值则表示该点的海拔高度，每一个局部极小值及其影响区域称为集水盆，而集水盆的边界则形成所谓的分水岭。分水岭的概念和形成可以通过模拟浸入过程来进行说明。在每一个局部极小值表面，刺穿一个小孔，然后把整个模型慢慢浸入水中，随着浸入的加深，每一个局部极小值的影响域慢慢向外扩展，在两个集水盆汇合处构筑大坝，即形成分水岭。分水岭的计算过程是一个迭代标注过程。分水岭比较经典的计算方法是  Vincent 提出的。在该算法中，分水岭计算分两个步骤，一个是排序过程，一个是淹没过程首先对每个像素的灰度级进行从低到高排序，然后在从低到高实现淹没过程中，对每一个局部极小值在 阶高度的影响域采用先进先出(FIFO)结构进行判断及标注。

      分水岭算法对微弱边缘具有良好的响应，图像中的噪声、物体表面细微的灰度变化，都会产生过度分割的现象。但同时应当看出，分水岭算法对微弱边缘具有良好的响应，是得到封闭连续边缘的保证的。另外，分水岭算法所得到的封闭的集水盆，为分析图像的区域特征提供了可能。为消除分水岭算法产生的过度分割，通常可以采用两种处理方法，一是利用先验知识去除无关边缘信息。二是修改梯度函数使得集水盆只响应想要探测的目标。为降低分水岭算法产生的过度分割，通常要对梯度函数进行修改，一个简单的方法是对梯度图像进行阈值处理，以消除灰度的微小变化产生的过度分割。

      程序可采用方法：用阈值来限制梯度图像以达到消除灰度值的微小变化产生的过度分割现象，获得适量的区域，再对这些区域的边缘点的灰度级进行从低到高排序，然后在从低到高实现淹没的过程，梯度图像则用 Sobel 算子计算获得。对梯度图像进行阈值处理时，选取合适的阈值对最终分割的图像有很大影响，因此阈值的选取是图像分割效果好坏的一个关键。这种方法的缺点是实际图像中可能含有微弱的边缘，灰度变化的数值差别不是特别明显，选取阈值过大可能会消去这些微弱边缘。

opencv中的分水岭算法函数：void watershed(InputArray image,InputOutputArray markers)要单独用好这个函数还是有点麻烦的，第一个参数必须是一个8bit 3通道彩色图像矩阵序列，第二个参数markers必须包含了种子点信息。后面实现的效果没有论文给的效果好，就不贴照片。