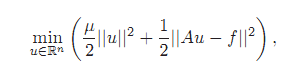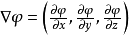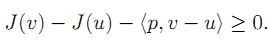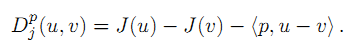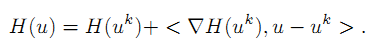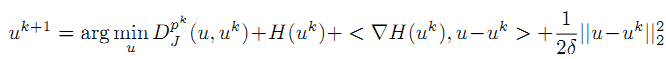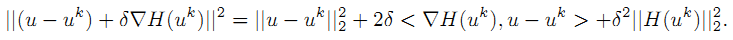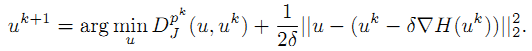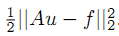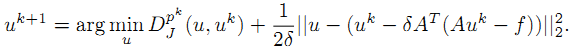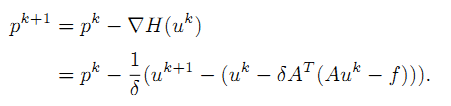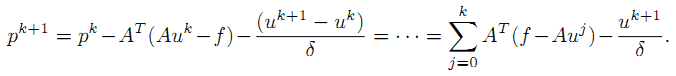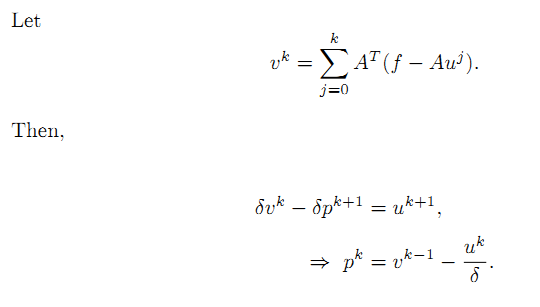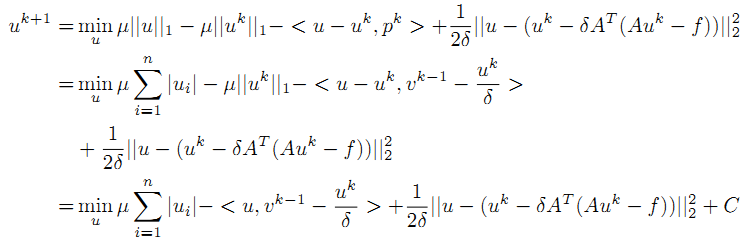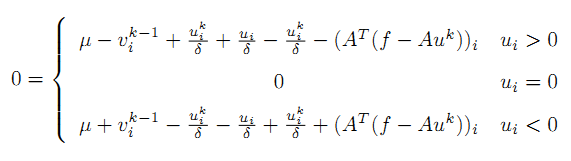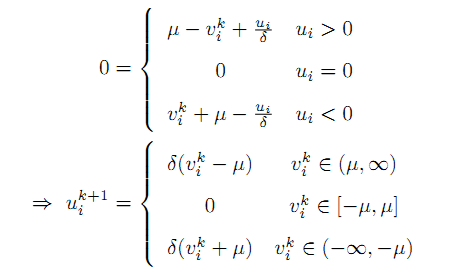凸优化中的Bregman迭代算法

本文主要是介绍凸优化中的Bregman迭代算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

http://blog.csdn.net/celerychen2009/article/details/9058315

对于搞图像处理的人而言，不懂变分法，基本上，就没法读懂图像处理的一些经典文献。当然，这已经是10年之前的事情了。

现在，如果不懂得Bregman迭代算法，也就没法读懂最近几年以来发表的图像处理的前沿论文了。国内的参考文献，基本上都是直接引用Bregman迭代算法本身，而对于其原理基本上找不到较为详细的论述。本文简要叙述当前流行的Bregman迭代算法的一些原理。

1、简介

近年来，由于压缩感知的引入，L1正则化优化问题引起人们广泛的关注。压缩感知，允许通过少量的数据就可以重建图像信号。L1正则化问题是凸优化中的经典课题，用传统的方法难以求解。我们先从经典的图像复原问题引入：

在图像复原中，一种通用的模型可以描述如下：
e.q.(1)

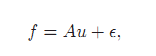
f：观测到的图像（m维向量）
u：未知的真实图像（n维向量）
A：线性算子，例如反卷积问题中的卷积算子，压缩感知中则是子采样测量算子。
：噪声，通常是高斯加性白噪声。方差为：sigma^2。
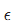
目标：由f得到u。

在式（1）中，我们仅知道观察到的图像f，其他的一概不知。因此这种问题是病态的，我们可以通过正则化把它变成良态的。

正则化方法：
假定对未知的参数 μ 引入一个先验的假设，例如稀疏性，平滑性。正则化问题的常见方法Tikhonov方法，它通过求解下面的优化问题：

其中 μ 是一个大于零的标量，事先设定的常数，用于权衡观测图像f和正则项之间的平衡。双绝对值符号是L2范数。L2条件约束。

下面，为了引入Bregman迭代算法，需要对两个重要的概念进行描述（次梯度和Bregman距离）。

2、Bregman距离

这里先复习一下梯度和导数的概念：

导数：lim(△x->0) ( f(x+△x) - f(x) ) / △x
方向导数：lim( dis(P0,P1) ->0) ( f(P1) - f(P0) ) / dis(P0,P1)。。上面讲的导数就是沿着 x 轴 方向的方向导数。
！！导数是 f(x) 在某个方向的变化率，是一个值，标量。

梯度：沿方向导数最大值的方向，大小为该方向导数的值。
！！梯度是一个向量。

次梯度

subgradient（次梯度，又称子梯度、弱梯度等），
泛函 J 在 u 点的次梯度定义如下：

J： X->R， 凸函数。
u：作用域X中的一点。
v：作用域 X 中的任一点。
p：X 的对偶空间 X* 的中的某一点。
： 是内积运算。如果泛函 J 是简单的一元函数，则就是两个实数相乘。

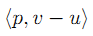
J 在 u 点的所有次梯度的集合成为 J 在 u 点的次微分，记为。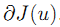

次梯度有什么好处呢？
对于一般的导数定义，例如 y=|x| 在0点是不可导的，但是对于次梯度，它是存在的。

Bregman距离

点u和v之间的Bregman距离定义如下：

J：X->R， 凸函数。
。。所以 p 是 J 在 u 点的一个次梯度。
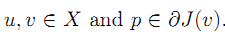
凸函数两个点u，v之间的Bregman距离：等于其函数值之差，再减去其次梯度点p与自变量之差的内积。

注意：这个距离不满足对称性，这和一般的泛函分析中距离定义是不一样的。

！！Bregman 距离有一些十分良好的性质，使得他在解决 L1 正则化问题时十分有效。

3、Bregman迭代算法

要解决的问题：求u(最小化)

Bregman迭代算法可以高效的求解下面的泛函的最小值问题。

J：X->R， 凸函数，非负。u∈X。
H：X->R， 凸函数，非负。u∈X，f 是已知常数（通常是一个观察得到的图像数据，是矩阵或向量）。
X：作用域，是凸集也是闭集。

注意：上述泛函会根据具体问题的不同具有不同的具体表达式。例如，对于简介中的图像复原问题， J(u) 是平滑先验约束，是正则化项；而H则是数据项。

Bregman迭代算法

首先，初始化相关的参数为零；
然后，再迭代公式u。。直到 uk 满足收敛条件。
u，左边一项是泛函 J 的Bregman距离。
p，右边一项是泛函 H 的梯度（？？？or次梯度？？？）。

可以看出：
· 第一次迭代，
u1=argmin(u) { D(u, 0) + H(u) }， 其中D(u, 0)=J(u) - J(0) - <0, u>=J(u)

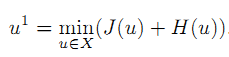
· 再经过多次的迭代，
就能够收敛到真实的最优解。

对于具体的问题:
定义的具体形式是不同的。
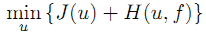
例如对于压缩感知使用的基追踪算法，J是L1范数；
而对于图像去噪问题，可能就是u的梯度L1范数，同时A也变成了恒等算子了。

4、线性Bregman迭代算法

Bregman算法对于基追踪问题来说是一种很好的工具。但是，算法中的每一步都要求解公式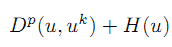的最小值，从而使得计算复杂度非常高。
因此提出了——

线性Bregman迭代算法推导

首先，利用矩阵的泰勒公式，将公式

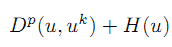
中的 H(u) 线性展开，得到：

但是这种近似展开只有在u和uk十分接近的时候上式才准确。因此，把泰勒公式中的二次项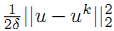加上，则原来的问题就变成了：

可以看到，二次项可以使 u 和 uk 很靠近。

为什么这里的二次项是L2范数的平方？
答：因为向量的平方就是L2范数的平方。。
？？？二阶导数不见了？？？？

又因为：

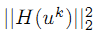
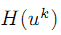
注意 和 是关于 u 的常数。

所以，

考虑基追踪算法，令 H(u) =

得到：

考虑该式的一个特殊情况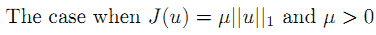， 。并将pk回代，得到：

C是一个常量，与uk有关的常量。uk也是一个常量。

分3种情况来考虑 u，则

进一步整理，得到：

定义shrink算子，当a>0时，有：

线性Bregman算法总结

5、Split Bregman 迭代算法

参考书：《Bregman算法》http://download.csdn.net/detail/celerychen2009/5552551

这篇关于凸优化中的Bregman迭代算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---