本文主要是介绍python生成树形图_P4716 朱刘算法/最小树形图/有向图最小生成树 python实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
遇到了一道题,一开始以为是简单的最小生成树
做完发现一直WA,学习了一下发现是朱刘算法,整理一下笔记
P4716 最小树形图
题目背景
这是一道模板题。
题目描述
给定包含 nnn 个结点, mmm 条有向边的一个图。试求一棵以结点 rrr 为根的最小树形图,并输出最小树形图每条边的权值之和,如果没有以 rrr 为根的最小树形图,输出 −1-1−1。
输入格式
第一行包含三个整数 n,m,rn,m,rn,m,r,意义同题目所述。
接下来 mmm 行,每行包含三个整数 u,v,wu,v,wu,v,w,表示图中存在一条从 uuu 指向 vvv 的权值为 www 的有向边。
输出格式
如果原图中存在以 rrr 为根的最小树形图,就输出最小树形图每条边的权值之和,否则输出 −1-1−1。
输入输出样例
输入 #1
4 6 1
1 2 3
1 3 1
4 1 2
4 2 2
3 2 1
3 4 1
输出 #1
3
输入 #2
4 6 3
1 2 3
1 3 1
4 1 2
4 2 2
3 2 1
3 4 1
输出 #2
4
输入 #3
4 6 2
1 2 3
1 3 1
4 1 2
4 2 2
3 2 1
3 4 1
输出 #3
-1
说明/提示
样例 111 解释
最小树形图中包含第 222, 555, 666 三条边,总权值为 1+1+1=31 + 1 + 1 = 31+1+1=3
样例 222 解释
最小树形图中包含第 333, 555, 666 三条边,总权值为 2+1+1=42 + 1 + 1 = 42+1+1=4
样例 333 解释
无法构成最小树形图,故输出 −1-1−1 。
数据范围
对于所有数据,1≤u,v≤n≤1001 \leq u, v \leq n \leq 1001≤u,v≤n≤100, 1≤m≤1041 \leq m \leq 10^41≤m≤104, 1≤w≤1061 \leq w \leq 10^61≤w≤106。
最小树形图
一个有向图,存在从某个点为根的,可以到达所有点的一个最小生成树,则它就是最小树形图。
简单来说,就是有向图的最小生成树
朱刘算法
为什么需要?
如果是无向图,用prim或者kruskal算法很简单
但是如果是有向图,就会有一些问题
举个例子
第一行包含三个整数n,m,r,意义同题目所述。
接下来m行,每行包含三个整数u, v, w,表示图中存在一从u指向V的权值为w的有向边。
对于所有数据,1≤u,v≤n≤100,1≤m≤10^4,1≤w≤10^6。
输入:
3 4 1
1 2 8
1 3 8
2 3 4
3 2 3

图画出来大概是这样子的,如果用prim算法的话就会和点的顺序有关。可能是11,可能是12
所以我们需要一个适用于有向图的算法
算法介绍
朱刘算法只有3步,然后不断循环。
找到每个点的最小入边。既然是生成树,那么对于每个点来说,只要选一个权值最小的入边就可以了。
贪心思想。因为如果不是最小入边,那么它肯定不是最小树形图的一条边,考虑它是没有意义的。
找环。找环找的是最小入边构成的新图的环。如果没找到环,那么一棵树就已经形成了,
因为树就是没有环的图。再因为边权都是最小的,因此此时最小树形图就已经出来了,停止循环。
如果第2步中找到了环,那么这个环就可以缩成一个点。然后构造新图,更新边权。
示意图大致如下:
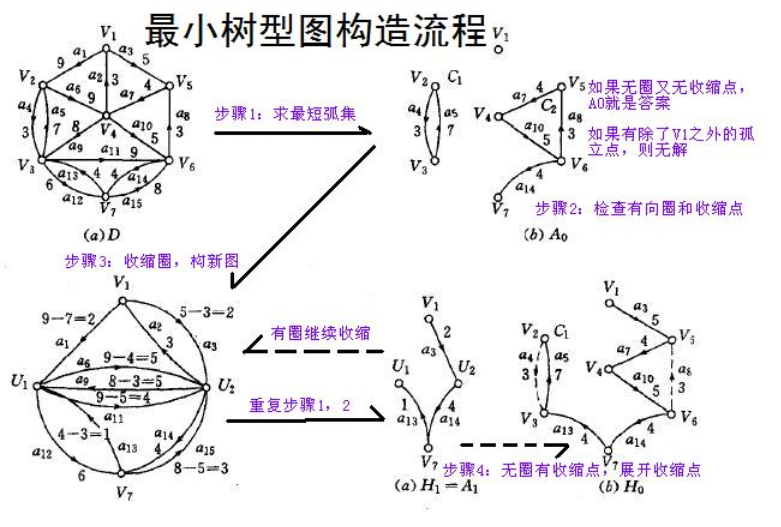
实现
class Edge:
def __init__(self, u, v, w):
self.u = u
self.v = v
self.w = w
def __str__(self):
return str(self.u) + str(self.v) + str(self.w)
def zhuliu(edges, n, m, root):
res = 0
while True:
pre = [-1]*n
visited = [-1] * n
circle = []
inderee = [INF] * n
# 寻找最小入边
inderee[root] = 0
for i in range(m):
if edges[i].u != edges[i].v and edges[i].w < inderee[edges[i].v]:
pre[edges[i].v] = edges[i].u
inderee[edges[i].v] = edges[i].w
# 有孤立点,不存在最小树形图
for i in range(n):
if i != root and inderee[i] == INF:
return -1
# 找有向h环
tn = 0 # 记录环的个数
circle = [-1] * n
for i in range(n):
res += inderee[i]
v = i
# 向前遍历找环,中止情况有:
# 1. 出现带有相同标记的点,成环
# 2. 节点属于其他环,说明进了其他环
# 3. 遍历到root了
while visited[v] != i and circle[v] == -1 and v != root:
visited[v] = i
v = pre[v]
# 如果成环了才会进下面的循环,把环内的点的circle进行标记
if v != root and circle[v] == -1:
while circle[v] != tn:
circle[v] = tn
v = pre[v]
tn += 1
# 如果没有环了,说明一定已经找到了
if tn == 0:
break
# 否则把孤立点都看作自环看待
for i in range(n):
if circle[i] == -1:
circle[i] = tn
tn += 1
# 进行缩点,把点号用环号替代
for i in range(m):
v = edges[i].v
edges[i].u = circle[edges[i].u]
edges[i].v = circle[edges[i].v]
# 如果边不属于同一个环
if edges[i].u != edges[i].v:
edges[i].w -= inderee[v]
n = tn
root = circle[root]
return res
INF = 9999999999
if __name__ == '__main__':
n, m, root = list(map(int, input().split()))
edges = []
for i in range(m):
u, v, w = list(map(int, input().split()))
# 输入的点是1开始的,-1改为0开始的
edges.append(Edge(u-1, v-1, w))
print(zhuliu(edges, n, m, root-1),end = "")
这篇关于python生成树形图_P4716 朱刘算法/最小树形图/有向图最小生成树 python实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








