GNN教程：Weisfeiler-Leman算法-GNN能力到底有多强呢？（GCN的逐层传播公式理解）

转载

目录

一、大纲

二、Weisfeiler-Leman 算法介绍

2.1 动机

2.2 Weisfeiler-Leman 算法思路

2.3 Weisfeiler-Leman 算法图形举例说明

三、Weisfeiler-Leman 算法与 GCN 间的转换

四、后话

参考

一、大纲

本文为GNN教程的第六篇文章 【Weisfeiler Leman算法】。前面的文章中，我们介绍了GNN的三个基本模型GCN、GraphSAGE、GAT，分析了经典的GCN逐层传播公式是如何由谱图卷积推导而来的。GNN模型现在正处于学术研究的热点话题，那么我们不经想问，GNN模型到底有多强呢？

我们的目的是分析GNN的表达能力，我们需要一个模型作为衡量标准。比如说如果我们想衡量GBDT的分类能力的话，通常情况下我们会使用同样的数据集，采用不同的分类模型如LR, RF, SVM等做对比。对于GNN模型，我们采用的对比模型叫做Weisfeiler-Leman，其常被用做图同构测试(Graph Isomorphism Test)，图同构测试即给定两个图，返回他们的拓扑结构是否相同。图同构问题是一个非常难的问题，目前为止还没有多项式算法能够解决它，而Weisfeiler-Leman算法是一个多项式算法在大多数case上能够奏效，所以在这里我们用它来衡量GNN的表达能力，这篇博文详细介绍了Weisfeiler-Leman算法，作为我们分析GNN表达能力的基础。

二、Weisfeiler-Leman 算法介绍

2.1 动机

Graph 的相似性问题是指判断给定两个 Graph 是否同构。如果两个图中对应节点的特征信息（attribute）和结构信息（structure）都相同，则称这两个图同构。因此我们需要一种高效的计算方法能够将的特征信息及结构位置信息(邻居信息)隐射到一个数值，我们称这个数值为节点的ID(Identification)。最后，两个图的相似度问题可以转化为两个图节点集合ID的 Jaccard 相似度问题。

2.2 Weisfeiler-Leman 算法思路

一般地，图中的每个节点都具有特征（attribute）和结构（structure）两种信息，需要从这两方面入手，来计算几点ID。很自然地，特征信息（attribute）即节点自带的Embedding，而结构信息可以通过节点的邻居来刻画，举个例子，如果两个节点Embedding相同，并且他们连接了Embedding完全相同的邻居，我们是无法区分这两个节点的，因此这两个节点ID相同。由此，可以想到，我们可以通过 hashing 来高效判断是否两个节点ID一致。1维的Weisfeiler-Lehman正是这样做的。

在上式中，F表示邻居Embedding的聚合函数，可以简单的将邻居Embedding排序后拼接起来(concatenate)。看到这里，有的读者可能产生了疑问，这个式子不是和之前GraphSAEG的跟新公式一样吗，那是不是意味着GraphSAGE具有和Weisfeiler-Leman算法相同的能力？确实这个式子在GraphSAGE中表示邻居节点的聚合(比如求和、Pooling等方式)，而Hash在GraphSAGE中是一个单层的感知机。这些差别实际上导致了GraphSAGE并没有完全的Weisfeiler-Leman算法的能力，在后一篇博文中我们会详细说明它。

下面我们通过一个形象的例子来说明Weisfeiler-Leman算法具体是如何操作的。

2.3 Weisfeiler-Leman 算法图形举例说明

给定两个图G和G' ，其中每个节点的Embedding为这个节点的标签（实际应用中，有些时候我们并拿不到节点的标签，这时可以对节点都标上一个相同的标签如"1"，这个时候我们将完全用节点位于图中的结构信息来区分节点，因为他们的Embedding都相同）

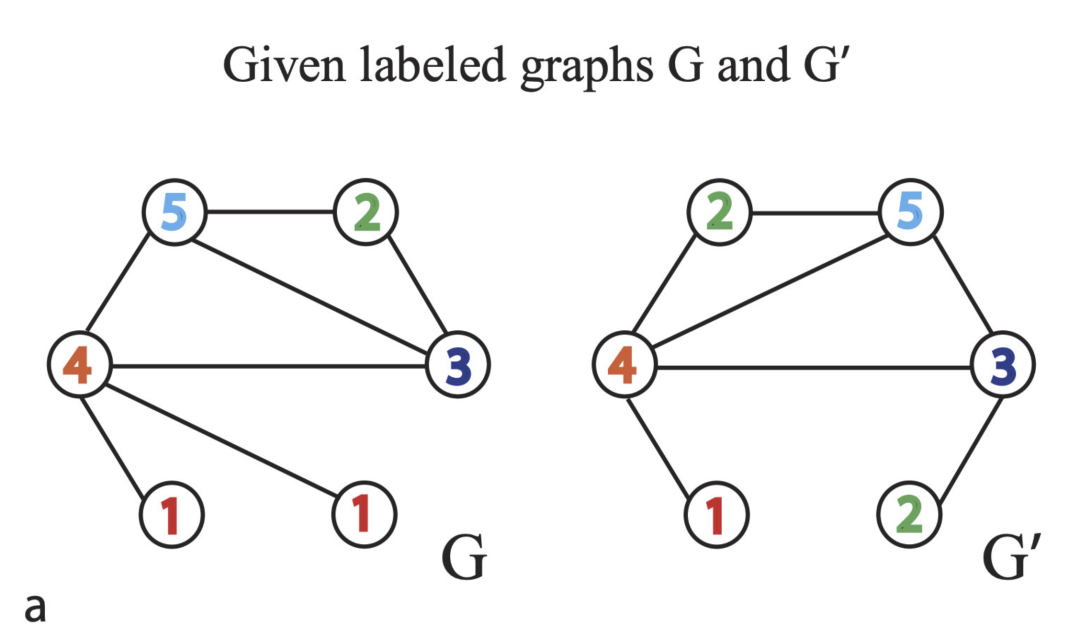
如何比较  G和 G'的相似性问题呢？Weisfeiler-lehman 算法的思路如下：

1、对邻居节点标签信息进行聚合，以获得一个带标签的字符串（整理默认采用升序排序的方法进行排序）。

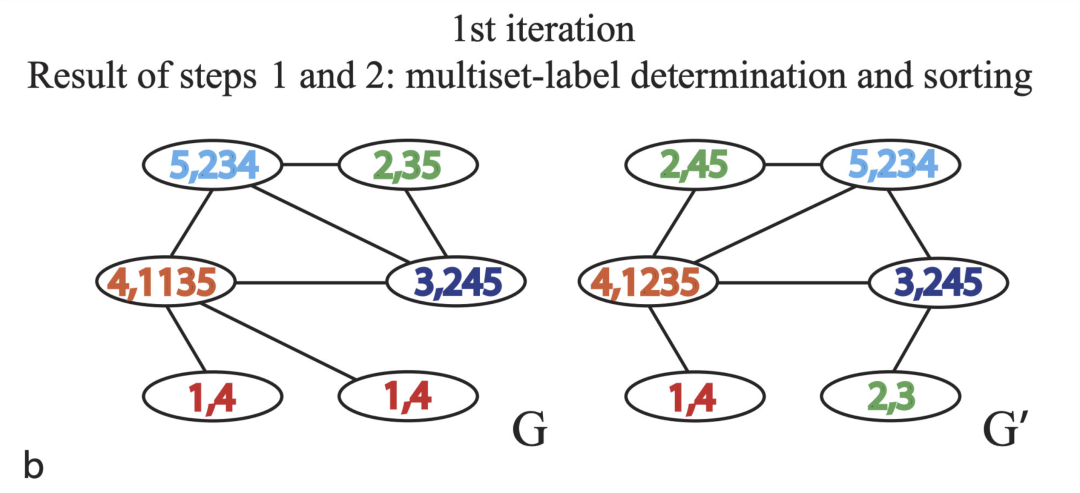
第一步的结果，这里需要注意，图中利用逗号将两部分进行分开，第一部分是该节点的ID，第二部分是该节点的邻居节点ID按升序排序的结构（eg：对于节点 5，他的邻居节点为2，3，4，所以他的结果为"5,234"）

2、为了能够生成一个一一对应的字典，我们将每个节点的字符串hash处理后得到节点的新ID。

3、将哈希处理过的ID重新赋值给相应的结点，以完成第一次迭代。

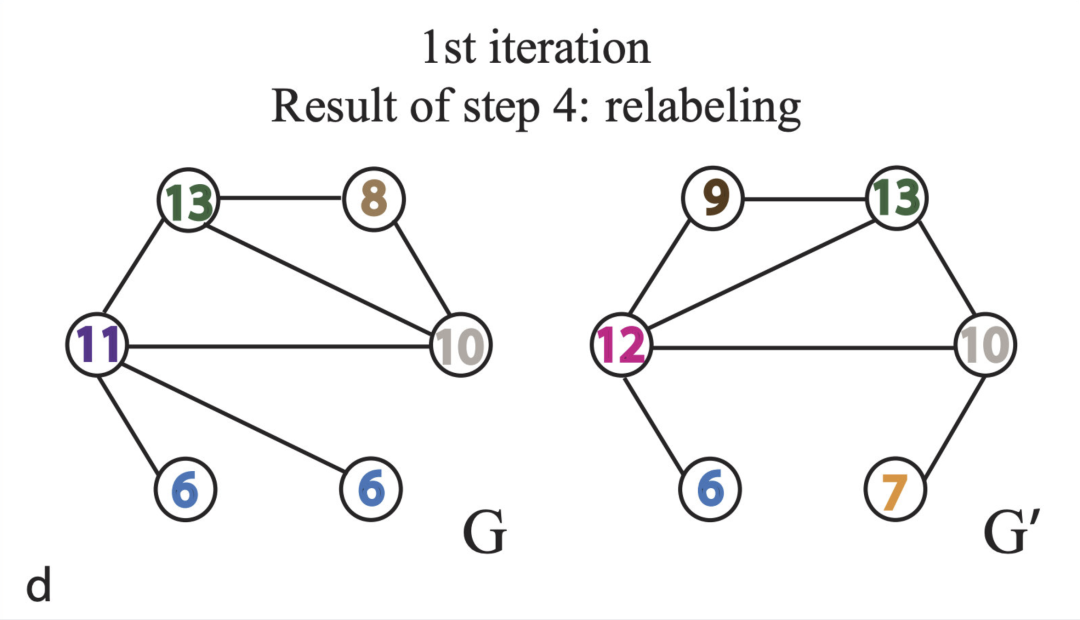
第一次迭代的结果为：

这样即可以获得图中每个节点ID。接下去，可以采用 Jaccard 公式计算G 和 G'的相似度。如果两个图同构的话，在迭代过程中和将会相同。

至此Weisfeiler-Leman算法就介绍完了，作为下一篇博文的引文，我们简要得分析一下Weisfeiler-Leman算法和GCN逐层更新公式的关系。

三、Weisfeiler-Leman 算法与 GCN 间的转换

GCN逐层更新公式为：

通过与 Weisfeiler-Lehman 算法的类比，我们可以理解即使是具有随机权重的未经训练的 GCN 模型也可以看做是图中节点的强大特征提取器。

四、后话

即使GCN、GraphSAGE、GAT和Weifeiler-Leman算法如此之像，但正如我们分析的那样，他们都做了一些近似，将Hash近似为单层感知机会导致一部分的精度损失，因为单层感知机不是单射函数。拼接邻居方式的近似引入了另一层精度损失，因为比如求和，pooling等邻居聚合方式可能作用于不同的邻居集合下而得到相同的结果，所以不管是哪个模型，都没有达到目前Weisfeiler-Leman算法在图同构问题上的能力。在下一篇博文中我们将会详细分析这些近似方法带来的损失，并给出如何解决这些问题。

参考

[1] SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS
[2] Weisfeiler-Lehman Graph Kernels
[3]《Graph learning》 图传播算法（下）