题目 1188: 做幻方

5
1
0

11 18 25  2  9
10 12 19 21  34  6 13 20 22
23  5  7 14 16
17 24  1  8 151

        其实这个题目降低了难度，Google一下你就知道，除了奇数次的幻方，还有偶数次的幻方，而且偶数次比奇数次难度要高出不少，而本题目仅要求输出奇数次，🙏感谢感谢。另外我采用的就是最原始的办法，一种一种情况去判断、去解决，网上大佬的代码秀得我头皮发麻(我啥时候能写出那种优美的代码😭😭），

代码就显得略长了一些，但是能保证大部分人一遍就看懂，如果不懂，Q1782356223！好了废话少说，开工！
        

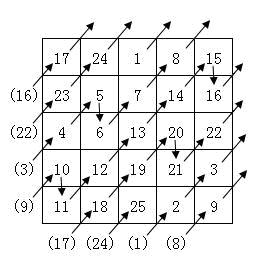
        我使用的是“楼梯法”，我结合着下面这张图说明一下！

        首先，我们先声明一个二维数组matrix[n][n](n是幻方的行数）；
        然后，把数字“1”放在第一行的中间位置，这个中间位置如何确定呢？答案就是n/2(n是幻方的行数），也就是matrix[0][n/2]

        然后，我们就依次将2、3、4、5、、、n 填入数组中，具体怎么个填充法？每个数字放在二维数组的哪个位置？这都要通过“楼梯法”解决问题。

        “楼梯法”的规则就是就是上图中箭头指的方向，在将其翻译成人话之前，请大家把上图中的二维数组的每一行、每一列都想像成一个个首尾相连的圆圈，也就是第一行是一个首尾相连的圆圈，这样以来，每一行、每一列的最后一个元素的下一个位置又重新回到了该行/该列的第一个元素位置，例如15的下一个位置是17、16的下一个位置是23，22的下一个位置是4；把列想像成一个圆圈，就会出现9的下一个位置是15、2的下一个位置是8、25的下一个位置1……

        然后把“楼梯法”翻译成人话就是：   “每次将一个数字填入上一个数字的右上方(比如上图中数字8填到了数字7的右上方，也就是 matrix[i-1][j+1] 的位置），如果上一个数字的右上方已经超出了二维数组的界限，例如，数字9应该填到数字8的右上方，但是8的右上方明显超出二维数组的界限, 这时就将其放到右上方所在行/列的第一个位置(8的右上方也就是15的上方就是第5列这个圆环上、15这个元素的下一个位置，由于圆圈首尾相连，15的下一个位置自然就是9所在的位置），同理17应该放到16的右上方，但是超出边界，则把17放到第一行的第一个位置。

        如果右上方没有超出边界，但是已经有元素存入其中(例如6应该放到5的右上方，但是该位置已经被1事先给占了)，这时就将元素放到上一个元素的下一个位置例如，5的右上方被占了，那就把6放到5的下方；21应该放到20的右上方，也就是16所在的位置，但是明显该位置已经被16给占了，所以把21放到20的下面。

        好了，以上就是“楼梯法”的规则了，简单来说就是一句话：新元素往上一个元素的右上角存，超出边界，则放到右上角所在的行/列的下一个位置，如果新元素位置已被占据，则存在上一个元素的下一个位置。

        
注意事项: 当新元素的位置超出边界时，我们要判断是行超出边界还是列超出边界，不同的原因对应着不同的解决方法，详见下方代码。

              另外，我确实没搞懂题目中的“右对齐”是怎么回事，所以就采用了最原始的方法进行打印输出，所以显得代码略长，但是能保证你看一遍就懂

参考代码:

#include <stdio.h>
#include <math.h>void create(int n) {if (n == 1) {//如果n等于1，直接输出printf("1\n\n");} else {//定义并初始化一下二维数组int matrix[n][n];for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {matrix[i][j] = 0;}}//开始构造幻方int i = 0, j = n / 2;//i、j作为每次填入元素的下标，i、j的值一直都在变，每一次都要判断是否已经超出二维数组的界限int k = 0, m = 0;//专门针对i和j都出现问题时所用matrix[0][n / 2] = 1;//先把1的位置摆在第一行正中央int key = 2;//key作为填入矩阵的数据，每次递增int count = 1;//计数器，当count等于n*n时表示二维数组已经填满，结束循环//一直循环到矩阵每一个位置都填充上数据，正好需要填充n*n次则结束循环while (1) {if (count == pow(n, 2)) {break;} else {//计数器还没到n*n次，说明还有空白位置，可以接着填入元素//按照"楼梯法"计算下一个数据元素的存储位置k = i;i -= 1;m = j;j += 1;//分别判断i、j是否超出了二维数组的表示范围if (i < 0 && j <= n - 1) {//i的问题，单独处理i：j保持不变，i=n+i;i = n + i;//i=-1时，n+i又跑到最后一行了//下标问题解决了，现在需要看该位置是否已经有元素填进去了if (matrix[i][j] == 0) {//等于0意味着该位置为空，可以填入matrix[i][j] = key;} else if (matrix[i][j] != 0) {//该位置已经不为空，不可填//将i、j恢复原状i = k;j = m;//恢复原状后，将新元素填写到非法位置的下一个i += 1;//j保持不变，i加1matrix[i][j] = key;}} else if (i >= 0 && j > n - 1) {//j的问题，单独处理j：i不变，j=n-j;j = n - j;//下标问题解决了，现在需要看该位置是否已经有元素填进去了if (matrix[i][j] == 0) {//等于0意味着该位置为空，可以填入matrix[i][j] = key;} else if (matrix[i][j] != 0) {//该位置已经不为空，不可填//将i、j恢复原状i = k;j = m;//恢复原状后，将新元素填写到非法位置的下一个i += 1;//j保持不变，i加1matrix[i][j] = key;}} else if (i < 0 && j > n - 1) {//i、j都出问题了,i、j都要做相应的处理i = n + i;j = n - j;//下标问题解决了，现在需要看该位置是否已经有元素填进去了if (matrix[i][j] == 0) {//等于0意味着该位置为空，可以填入matrix[i][j] = key;} else if (matrix[i][j] != 0) {//该位置已经不为空，不可填//将i、j恢复原状i = k;j = m;//恢复原状后，将新元素填写到非法位置的下一个i += 1;//j保持不变，i加1matrix[i][j] = key;}} else {//i、j都没出问题，一切正常，万事大吉，正常操作，将新的key存入新的matrix[i][j]//下标问题解决了，现在需要看该位置是否已经有元素填进去了if (matrix[i][j] == 0) {//等于0意味着该位置为空，可以填入matrix[i][j] = key;} else if (matrix[i][j] != 0) {//该位置已经不为空，不可填//将i、j恢复原状i = k;j = m;//恢复原状后，将新元素填写到非法位置的下一个i += 1;//j保持不变，i加1matrix[i][j] = key;}}//填完一个数字后，将key值加1，为下一次的填充作准备key++;//count也要加1，表示又有一个数字填充进数组count++;}}//题目要求倒着输出，即先输出最后一行，再输出倒数第二行...屁事真多,还得右对齐，我艹if (pow(n, 2) < 10) {for (int l = n - 1; l >= 0; --l) {for (int i1 = 0; i1 < n; ++i1) {printf("%d ", matrix[l][i1]);}//输完一行，另起一行printf("\n");}} else if (pow(n, 2)>= 10 && pow(n, 2) <= 99) {for (int l = n - 1; l >= 0; --l) {for (int i1 = 0; i1 < n; ++i1) {if (matrix[l][i1] < 10) {printf(" %d", matrix[l][i1]);} else if (matrix[l][i1] >= 10 && matrix[l][i1] <= 99) {printf("%d", matrix[l][i1]);}printf(" ");}//输完一行，另起一行printf("\n");}} else if (pow(n, 2) >= 100) {for (int l = n - 1; l >= 0; --l) {for (int i1 = 0; i1 < n; ++i1) {if (matrix[l][i1] < 10) {printf("  %d", matrix[l][i1]);} else if (matrix[l][i1] >= 10 && matrix[l][i1] <= 99) {printf(" %d", matrix[l][i1]);} else if (matrix[l][i1] >= 100) {printf("%d", matrix[l][i1]);}printf(" ");}//输完一行，另起一行printf("\n");}}//输完一组，输出一个空行用于输出下一个幻方printf("\n");}}int main() {int n = 0;while (~scanf("%d", &n) && n) {create(n);}return 0;
}