t-SNE算法的基本思想及其Python实现

    t-SNE全称为t-distributed Stochastic Neighbor Embedding，翻译为t-随机邻近嵌入，它是一种嵌入模型，能够将高维空间中的数据映射到低维空间中，并保留数据集的局部特性，该算法在论文中非常常见，主要用于高维数据的降维和可视化。提出论文为：Visualizing Data using t-SNE。
    t-SNE可以算是目前效果最好的数据降维和可视化方法之一，当我们想对高维数据集进行分类，但又不清楚这个数据集有没有很好的可分性（同类之间间隔小、异类之间间隔大）时，可以通过t-SNE将数据投影到2维或3维空间中观察一下：如果在低维空间中具有可分性，则数据是可分的；如果在低维空间中不可分，则可能是因为数据集本身不可分，或者数据集中的数据不适合投影到低维空间。
    t-SNE将数据点之间的相似度转化为条件概率，原始空间中数据点的相似度由高斯联合分布表示，嵌入空间中数据点的相似度由学生t分布表示。通过原始空间和嵌入空间的联合概率分布的KL散度（用于评估两个分布的相似度的指标，经常用于评估机器学习模型的好坏）来评估嵌入效果的好坏，即将有关KL散度的函数作为损失函数（loss function），通过梯度下降算法最小化损失函数，最终获得收敛结果。要注意t-SNE的缺点很明显：占用内存较多、运行时间长。
    下面参考这篇博客中的代码看一下t-SNE的效果：数据降维与可视化——t-SNE

1 降维
    首先，通过一个简单的示例看一下t-SNE的降维效果：输入4个5维的数据，通过t-SNE将其降维成2维的数据，代码如下：

import numpy as np
from sklearn.manifold import TSNE"""将3维数据降维2维"""# 4个3维的数据
x = np.array([[0, 0, 0, 1, 2], [0, 1, 1, 3, 5], [1, 0, 1, 7, 2], [1, 1, 1, 10, 22]])
# 嵌入空间的维度为2，即将数据降维成2维
ts = TSNE(n_components=2)
# 训练模型
ts.fit_transform(x)
# 打印结果
print(ts.embedding_)

        结果如图所示：


2 S型曲线的降维与可视化
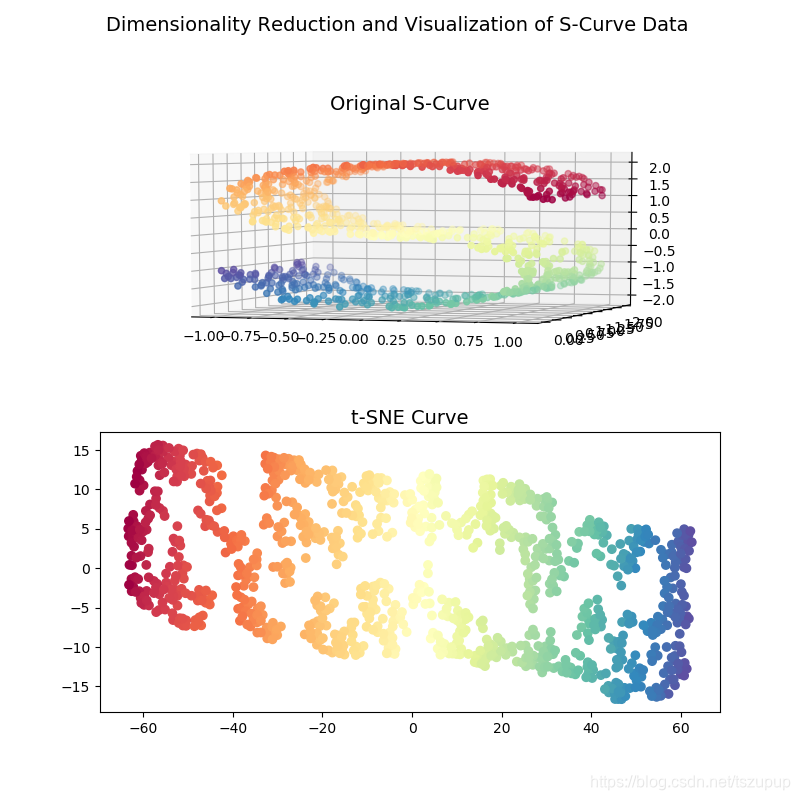
    S型曲线中的数据是高维的数据，不同的颜色表示不同的数据点。当我们通过t-SNE将数据嵌入到2维空间中后，可以看到数据点之间的类别信息被完整地保留了下来。代码如下：

import matplotlib.pyplot as plt
from sklearn import manifold, datasets"""对S型曲线数据的降维和可视化"""# 生成1000个S型曲线数据
x, color = datasets.samples_generator.make_s_curve(n_samples=1000, random_state=0)		# x是[1000,2]的2维数据，color是[1000,1]的一维数据n_neighbors = 10
n_components = 2# 创建自定义图像
fig = plt.figure(figsize=(8, 8))		# 指定图像的宽和高
plt.suptitle("Dimensionality Reduction and Visualization of S-Curve Data ", fontsize=14)		# 自定义图像名称# 绘制S型曲线的3D图像
ax = fig.add_subplot(211, projection='3d')		# 创建子图
ax.scatter(x[:, 0], x[:, 1], x[:, 2], c=color, cmap=plt.cm.Spectral)		# 绘制散点图，为不同标签的点赋予不同的颜色
ax.set_title('Original S-Curve', fontsize=14)
ax.view_init(4, -72)		# 初始化视角# t-SNE的降维与可视化
ts = manifold.TSNE(n_components=n_components, init='pca', random_state=0)
# 训练模型
y = ts.fit_transform(x)
ax1 = fig.add_subplot(2, 1, 2)
plt.scatter(y[:, 0], y[:, 1], c=color, cmap=plt.cm.Spectral)
ax1.set_title('t-SNE Curve', fontsize=14)
# 显示图像
plt.show()

    效果如下图所示：



3 手写数字数据集的降维与可视化
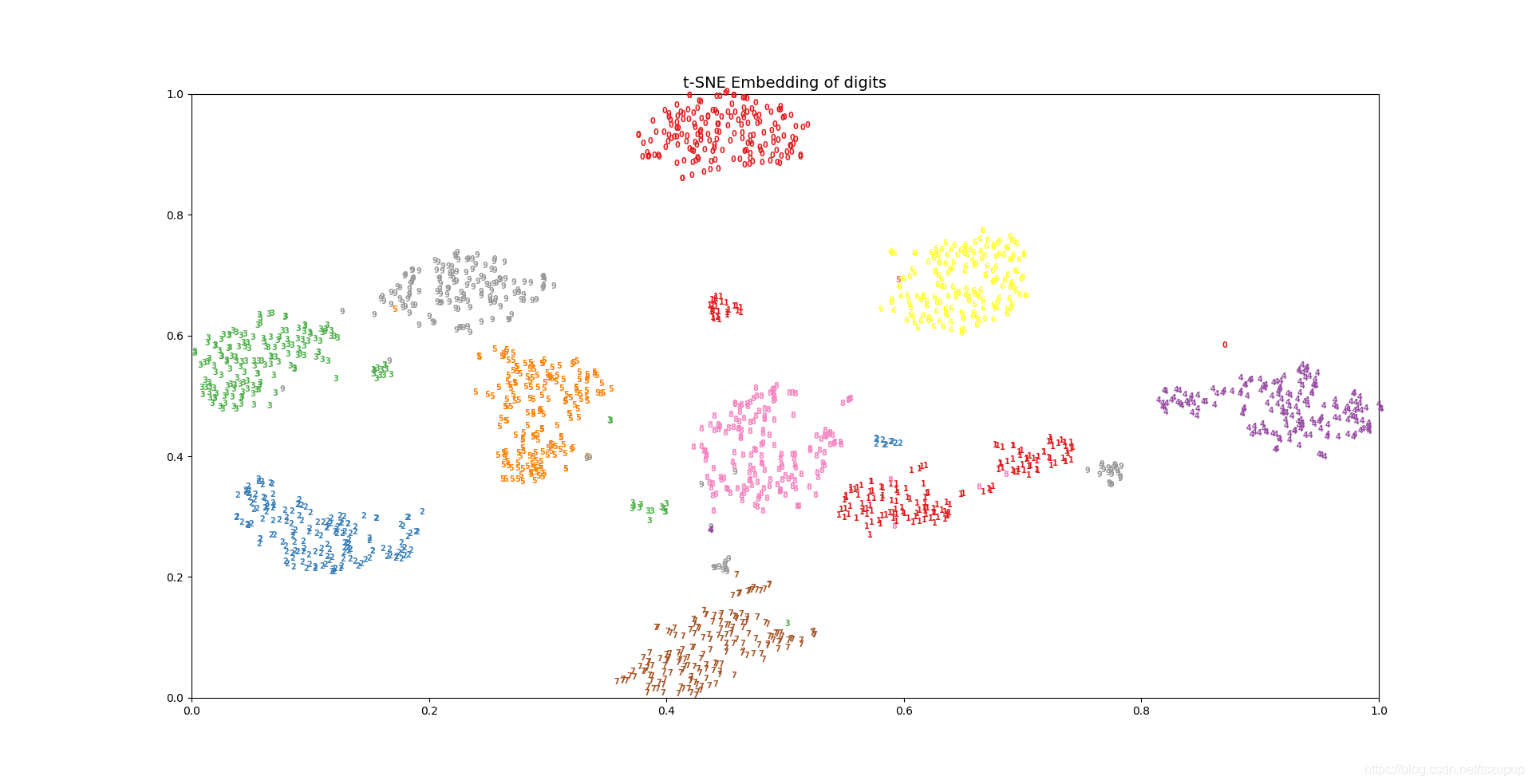
    手写数字数据集是一个经典的图片分类数据集，数据集中包含0-9这10个数字的灰度图片，每张图片以8*8共64个像素点表示。具体代码如下：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.manifold import TSNE# 加载数据
def get_data():""":return: 数据集、标签、样本数量、特征数量"""digits = datasets.load_digits(n_class=10)data = digits.data		# 图片特征label = digits.target		# 图片标签n_samples, n_features = data.shape		# 数据集的形状return data, label, n_samples, n_features# 对样本进行预处理并画图
def plot_embedding(data, label, title):""":param data:数据集:param label:样本标签:param title:图像标题:return:图像"""x_min, x_max = np.min(data, 0), np.max(data, 0)data = (data - x_min) / (x_max - x_min)		# 对数据进行归一化处理fig = plt.figure()		# 创建图形实例ax = plt.subplot(111)		# 创建子图# 遍历所有样本for i in range(data.shape[0]):# 在图中为每个数据点画出标签plt.text(data[i, 0], data[i, 1], str(label[i]), color=plt.cm.Set1(label[i] / 10),fontdict={'weight': 'bold', 'size': 7})plt.xticks()		# 指定坐标的刻度plt.yticks()plt.title(title, fontsize=14)# 返回值return fig# 主函数，执行t-SNE降维
def main():data, label , n_samples, n_features = get_data()		# 调用函数，获取数据集信息print('Starting compute t-SNE Embedding...')ts = TSNE(n_components=2, init='pca', random_state=0)# t-SNE降维reslut = ts.fit_transform(data)# 调用函数，绘制图像fig = plot_embedding(reslut, label, 't-SNE Embedding of digits')# 显示图像plt.show()# 主函数
if __name__ == '__main__':main()

    效果截图如下：

References:
数据降维与可视化——t-SNE