本文主要是介绍从2-3-4叉树到红黑树(下)--java集合源码体系研究之基础,让你面试胖揍面试官,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
源码分享说明
-
本人非常热衷于源码研究,同时也非常愿意将自己在源码方面研究的心得进行分享,如果读者也想对源码进行研究,可以关注我的分享的文章。
-
在进行源码解析的过程中,将会选择庖丁解牛式的剖析,将会解析清楚每一行核心代码,让读者能够真正透彻理解,这样无论是在以后的面试中还是独立开发中间件都会有很大好处。
序言
-
只要读者要毅力能够坚持下来,将笔者所描述的内容弄明白,无论是对于数据结构还是源代码的阅读能力都会有很大的帮助,真正提升你代码能力的内功,从下节开始,将真正分析Java核心容器类的源代码,展示出对应数据结构是怎样在Java中进行落地的
-
为了将hashmap,treemap源码彻底讲清楚,本人还是花费不少心血,从位运算介绍开始,让读者清楚现实中的数据在计算机中是怎样表示的,同时通过具体示例说明加深读者对位运算的理解。hashmap,treemap这两个底层都会使用到红黑树这种数据结构,为了更好的说明红黑树的性质以及他的前世今生,通过图片中具体示例形象的展示了每一个概念
-
本小节主要通过图形的形式形象的描述2-3-4树与红黑树的等价关系,可以说你对2-3-4树掌握得有多深入,就决定你对红黑树能够理解得有多深入,比如对于红黑树在新增或者删除后怎样进行调整就完全取决于你对2-3-4树进行新增或者删除后怎样进行调整,所以读者需要好好去深入理解上一小节关于2-3-4树讨论
-
首先给出红黑树本身的5大性质,新增节点,删除节点红黑为了保持平衡性质而所做的调整,通过对2-3-4树的操作,给出红黑树从初始状况到最终平衡中的每一步,让读者真正意义上的理解红黑树,而不是仅仅只是死记红黑树新增/删除通过怎样操作才能够重新保存平衡的结论。将枯燥无味的结论充实起来,从而变得有血有肉。希望读者能够多阅读几遍,彻底理解2-3-4树以及红黑树整个操作流程,可以毫不夸张的说,只要你真正理解了本小节里面的内容,在阅读Java容器类中关于红黑树方面的源代码你将会是得心应手。本小节不会展示代码,后面我们在分析hashmap,treemap源码的时候会详细解析每一步操作在代码中是怎样落地的
(1).2-3-4树和红黑树的等价关系
(1.1)2-3-4树与红黑树单节点转化关系
(1.1.1)一个二节点对应红黑树一个黑色节点
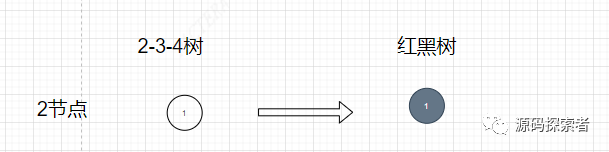
(1.1.2)一个三节点可以对应两种红黑树节点,上面节点黑色,下面节点红色,但是可以有两种形态,一种是右倾,一种是左倾,这个导致2-3-4树转化为多钟不同形态的红黑树
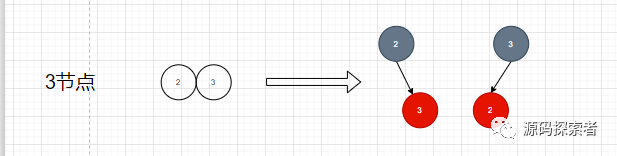
(1.1.3)一个四节点对应红黑树情况,中间节点黑色,左右节点红色
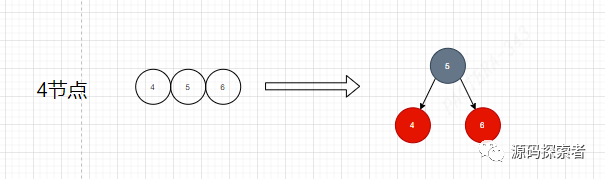
(1.1.4)下图展示了在四节点中添加节点导致违背了2-3-4树节点性质,所进行调整的完整过程
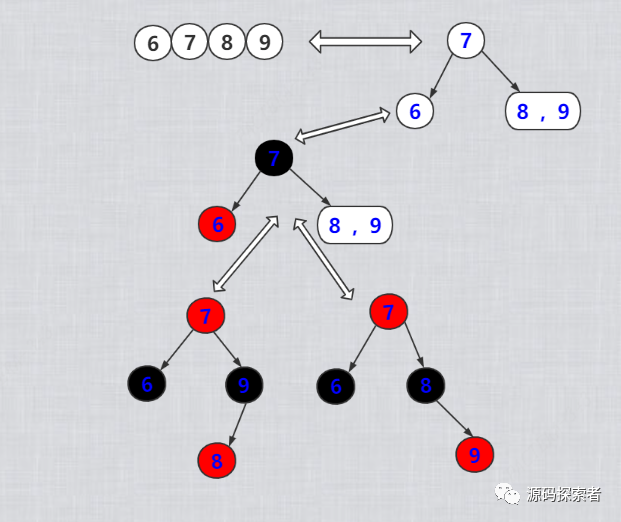
(1.2)整个2-3-4叉树与红黑树转化关系
(1.2.1)假如初始2-3-4树如下图所示
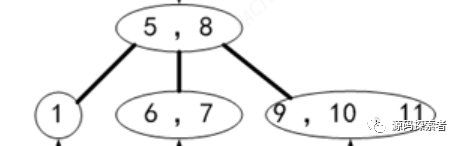
(1.2.2)初始2-3-4树与第一种形式红黑树相互转化过程(3节点右倾)
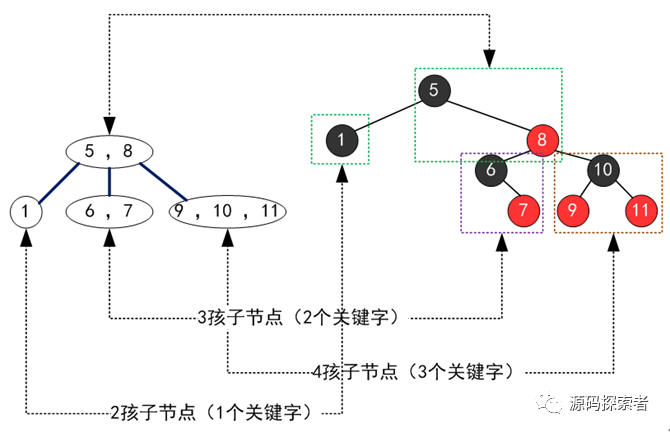
(1.2.3)初始2-3-4树与第另一种形式红黑树相互转化过程(3节点左倾)
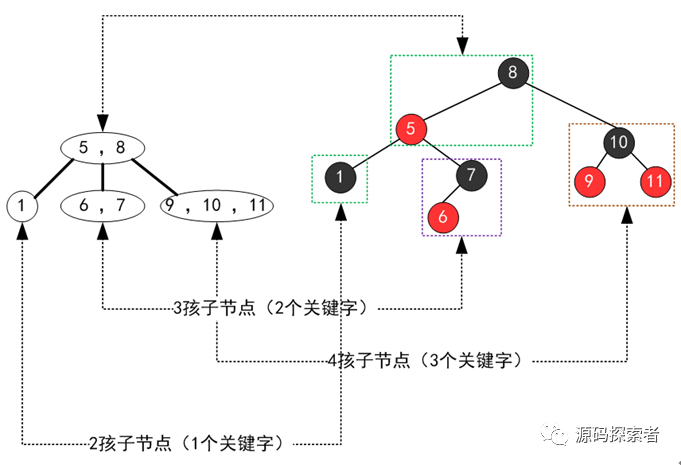
(1.2.4)如上两图所示,同一颗2-3-4树转化为多种形式的红黑树,就是因为三节点有两种转化形式引起的,但是一颗红黑树只能转化为一颗2-3-4树
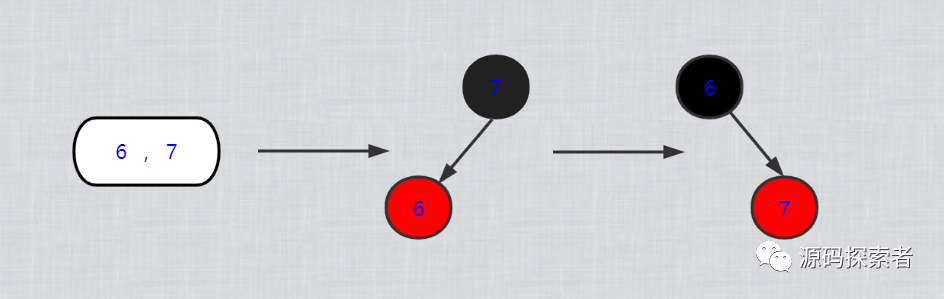
(2).红黑树定义
-
结点是红色或黑色
-
根节点是黑色
-
所有叶子都是黑色(叶子是NIL结点)
-
每个红色结点的两个子结点都是黑色(从每个叶子到根的所有路径上不能有两个连续的红色结点)
-
从任一节结点其每个叶子的所有路径都包含相同数目的黑色节点
通过2-3-4叉树和红黑树等价关系,我们很容易通过2-3-4树推导出红黑树五大性质
推导:
1、结点是红色或黑色:这个基本是废话,结点本来就要么是红色要么是黑色
2、根节点是黑色:2-3-4树只有三种节点,根节点要么是2节点,要么是3节点,要么是4节点。无论那种节点,根据等价关系,根节点都是黑色的,所以红黑树具有根节点是黑色这个性质
3、所有叶子都是黑色(叶子是NIL结点):在2-3-4树中,我们知道2节点、3节点、4节点含义,直观上觉得他们下一层是没有子节点,其实不然,他们下面挂了空节点(NIL,JAVA中是null),只是图中没有画出来而已,单独的null节点是一个特殊的2节点,根据等价关系,自然所有的叶子都是黑色的(这一点其实很重要,不然导致treemap,hashmap中红黑树添加/删除节点无法理解)
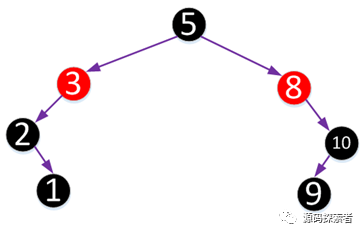
看上面这张图,如果不使用黑哨兵,它完全满足红黑树性质,根结点5到两个叶结点1和叶结点9路径上的黑色结点数都为3个,且没有连续红色节点。
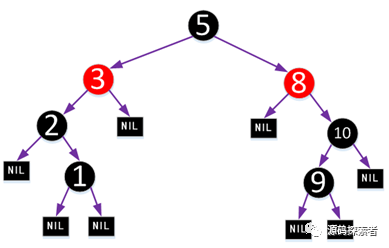
但如果加入黑哨兵后,叶结点的个数变为8个黑哨兵,根结点5到这8个叶结点路径上的黑高度就不一样了,所以它并不是一棵红黑树。
4、每个红色结点的两个子结点都是黑色(从每个叶子到根的所有路径上不能有两个连续的红色结点):根据性质3,如果是2-3-4树上最后一层上的节点,则根据等价关系,红色节点下方一定挂着两个黑色的空节点。如果不是最后一层上的节点,由2-3-4树节点性质可知,下方一定挂着不为空的节点(起码是2节点,根据等价关系一定是上黑下红),所以红色节点下方还是有两个黑色子节点
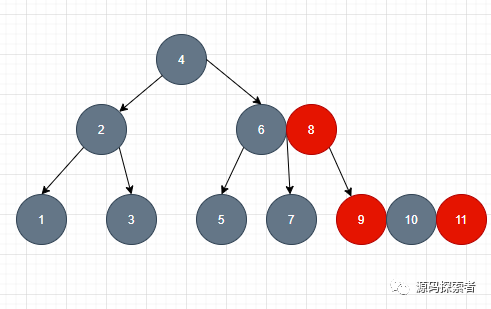
5、从任一节结点其每个叶子的所有路径都包含相同数目的黑色节点:这个可以由一张图来解释,2-3-4树种每一个节点中都会有一个元素被黑色标记,根据等价关系转换后,自然每一条路径的黑色节点数都是相同的
(3).红黑树的插入操作
-
如果红黑树中已存在待插入的值,那么插入操作失败,否则一定是在叶子节点进行插入操作,执行步骤2。
-
当我们插入一个新节点后,我们会把该节点涂红(经过整体测试,新增节点为红色比为黑色,为了维持树平衡,需要更少旋转次数),插入操作可能破坏了红黑树的平衡性(新增节点和父节点都是红色),所以需要不断向上回溯,进行调整。其实就是颜色变换和旋转操作,而这些操作都可以从2-3-4树来理解。考虑到回溯的情况,为了便于理解,同时2-3-4树与红黑树等价,我们以2-3-4树进行操作,我们可以把X节点看成向上层进位的key。
(3.1) 黑父
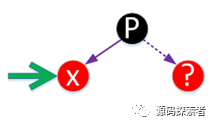
红黑树处理:插入后直接涂红,如果父亲节点是个黑色,插入结束。
2-3-4树处理:相当于2-3-4树中待插入的叶子节点是个2节点(对应黑父没有孩子节点)或者3节点(黑父有孩子节点,孩子节点的颜色一定是红色)。
(3.2) 红父黑叔
红黑树处理:下面四张图列出了4种不同场景新增节点为了重新保持平衡而进行的调整方法
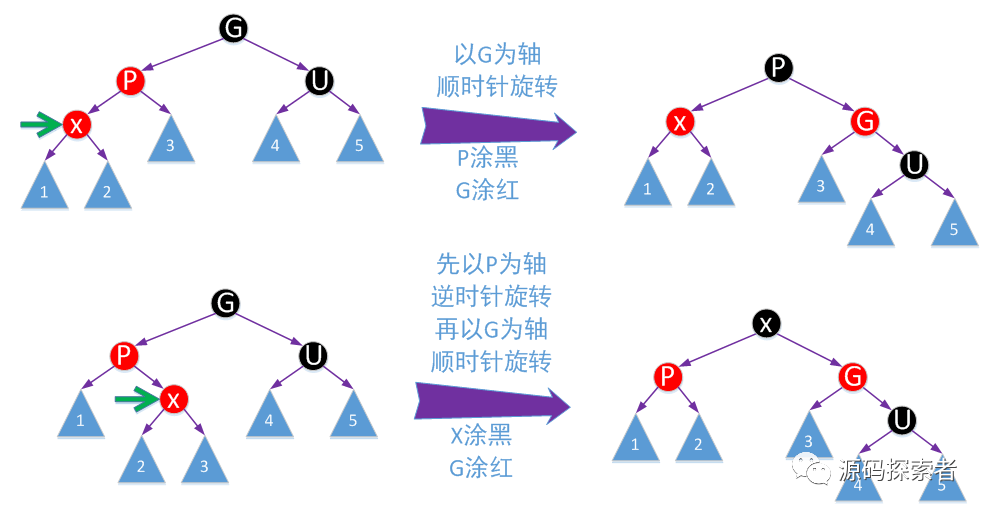
还有对应镜像情况,即P为G右子支,通过对称处理就可以
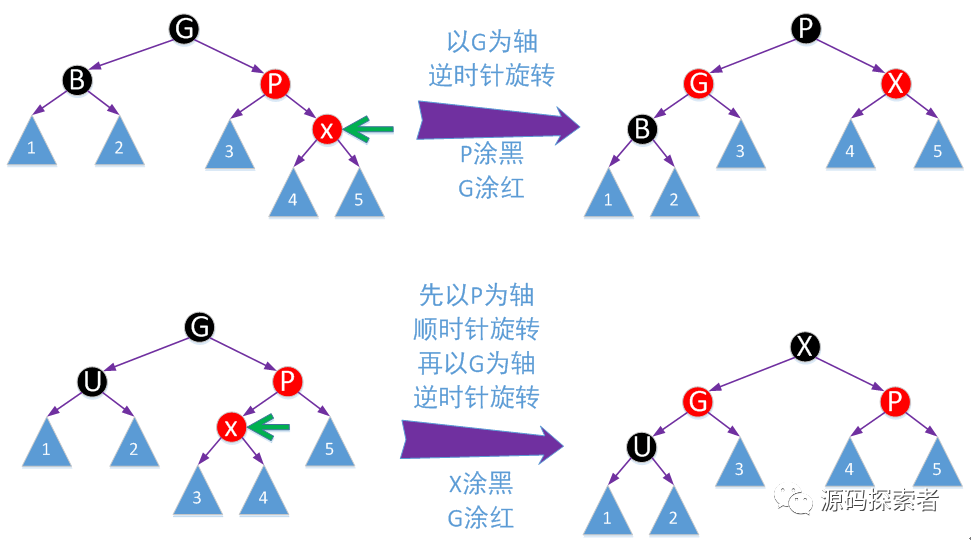
2-3-4树处理:以如下这个为例,其他读者自行推演,只要读懂这个,其他应该是可以自己搞定的
红黑树
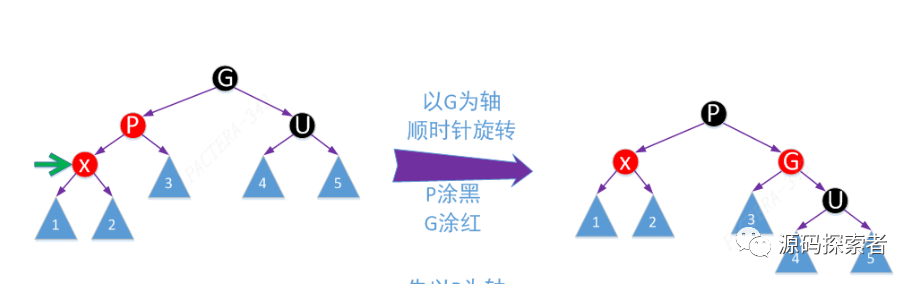
2-3-4树演变过程
对应2-3-4树中,容纳进位的父节点为3节点,还有空间可以容纳key,所以到此就不用继续回溯了。
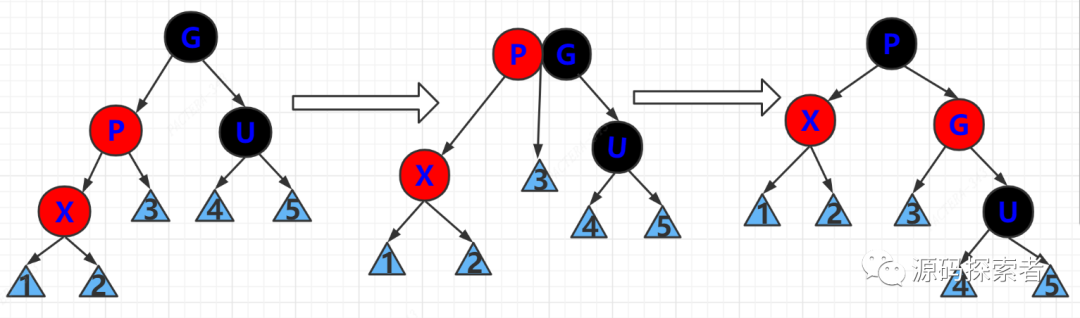
(3.3) 红父红叔
红黑树处理:下面四张图列出了2种不同场景新增节点为了重新保持平衡而进行的调整方法
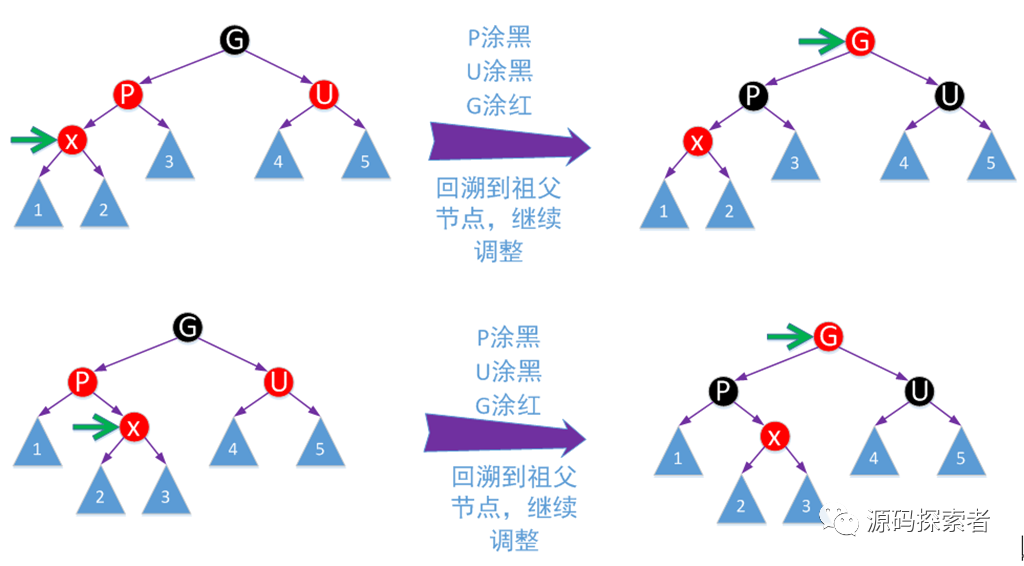
2-3-4树处理:以如下这个为例,其他读者自行推演,只要读懂这个,其他应该是可以自己搞定的
红黑树
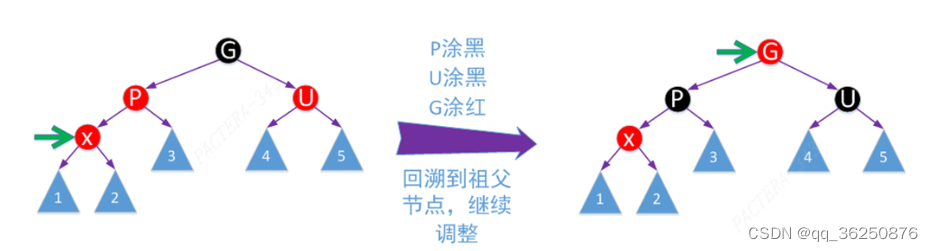
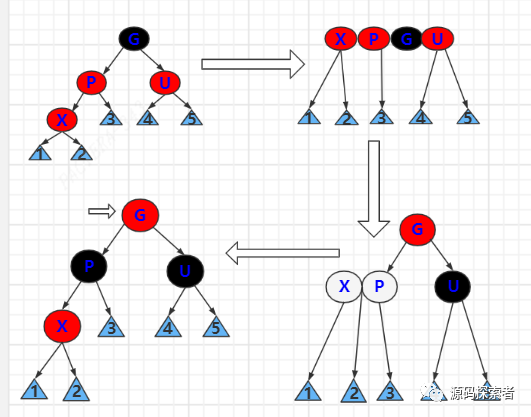
2-3-4树演变过程
对应2-3-4树中,向上进位的父节点为4节点,所以先分裂(对应P和B的颜色变换)然后再插入X,然后继续回溯,把G看成向更上一层进位的节点(即把G看成新的X)
(4). 红黑树的删除操作
-
查找要删除的值所在的节点,如果不存在,删除失败,否则执行步骤2
-
如果要删除的节点不是叶子节点,用要删除节点的后继节点替换(只进行数据替换即可,颜色不变,此时不需要调整结构),然后删除后继节点。
(4.1)要删除节点为红色
红黑树处理:直接删除当前节点X

2-3-4树处理:这个很明显,基本上不需要解释
(4.2)要删除的节点为黑色,且有一个孩子节点,这个孩子节点必然为红色
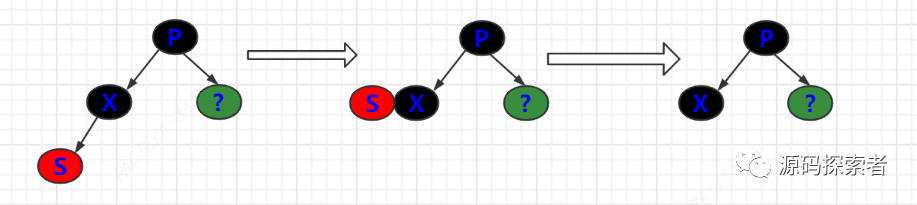
红黑树处理:下面四张图列出了2种不同场景删除节点为了重新保持平衡而进行的调整方法
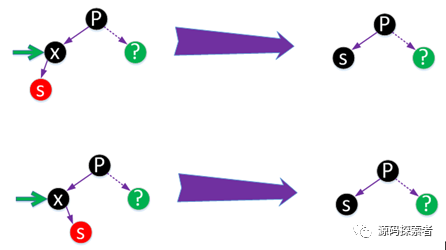
2-3-4树处理:以如下这个为例,其他读者自行推演,只要读懂这个,其他应该是可以自己搞定的
红黑树

2-3-4树演变过程
(4.3)要删除的节点为黑色,孩子节点都NIL
删除这个黑色节点后需要进行调整,在图中X总表示下一层的节点,一开始X表示NIL节点(回溯过程中X会不断向上层迭代)。
(4.3.1)黑兄红侄
红黑树处理:下面四张图列出了4种不同场景删除节点为了重新保持平衡而进行的调整方法
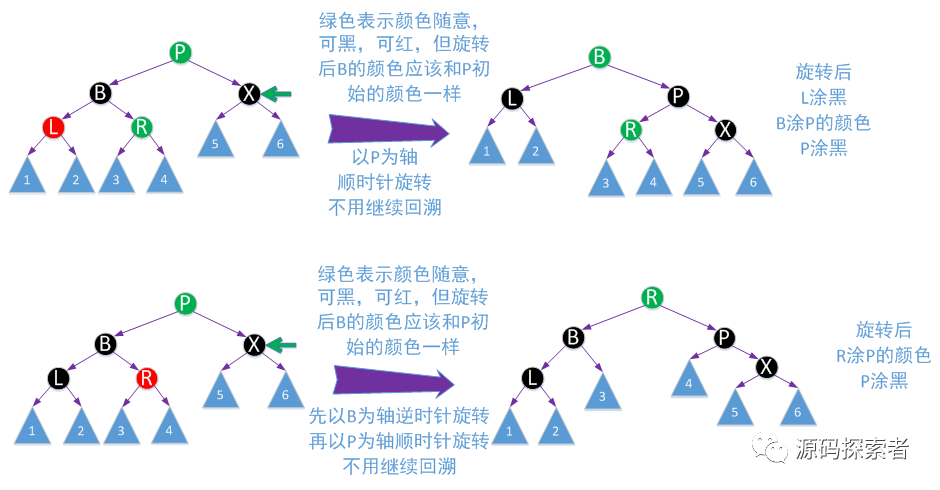
还有对应镜像情况,即P为G右子支,通过对称处理就可以
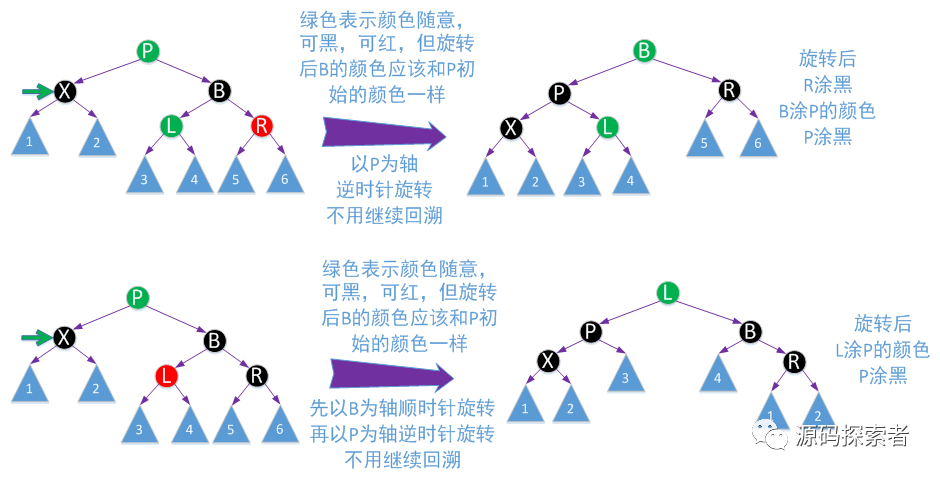
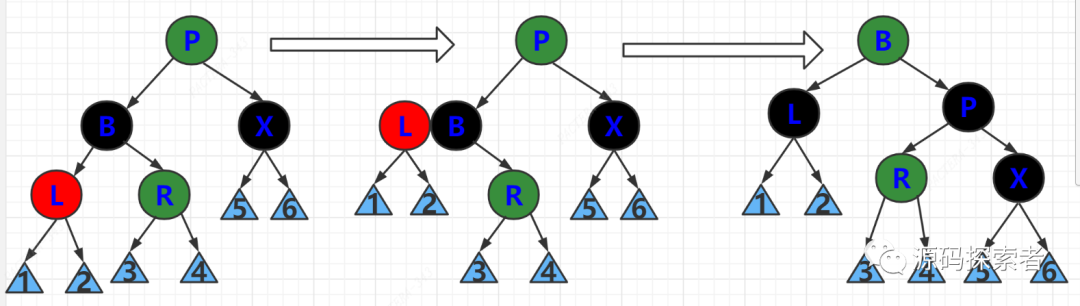
2-3-4树处理:以如下这个为例,其他读者自行推演,只要读懂这个,其他应该是可以自己搞定的
红黑树
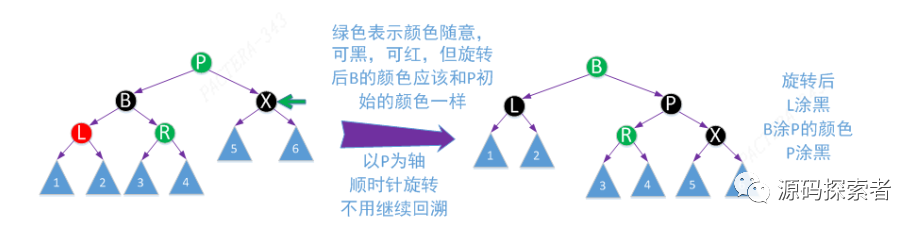
2-3-4树演变过程
对应2-3-4树删除操作中兄弟节点为3节点或4节点,父节点key下移,兄弟节点key上移动
(4.3.2)黑兄黑侄红父
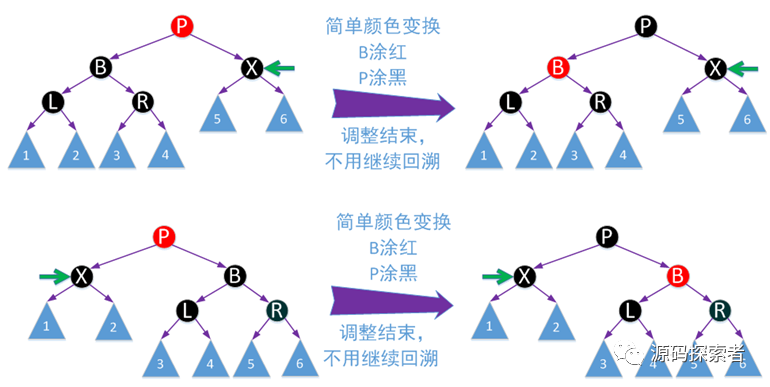
红黑树处理:下面四张图列出了2种不同场景删除节点为了重新保持平衡而进行的调整方法
2-3-4树处理:以如下这个为例,其他读者自行推演,只要读懂这个,其他应该是可以自己搞定的
红黑树
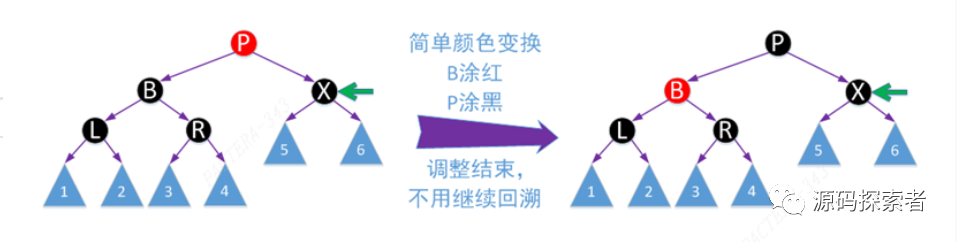
2-3-4树演变过程
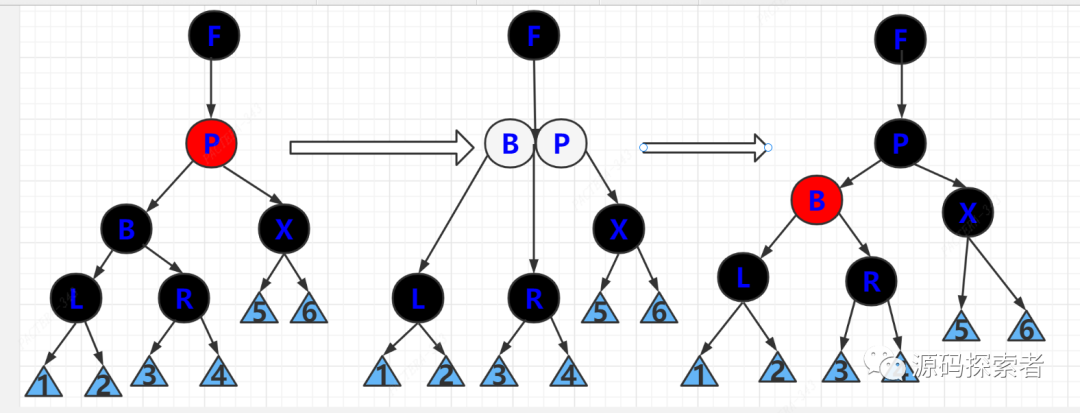
对应2-3-4树删除操作中兄弟节点为2节点,父节点至少是个3节点,父节点key下移与兄弟节点合并。
通过引入一个父节点F帮助理解
(4.3.3)黑兄黑侄黑父
红黑树处理:下面四张图列出了2种不同场景删除节点为了重新保持平衡而进行的调整方法
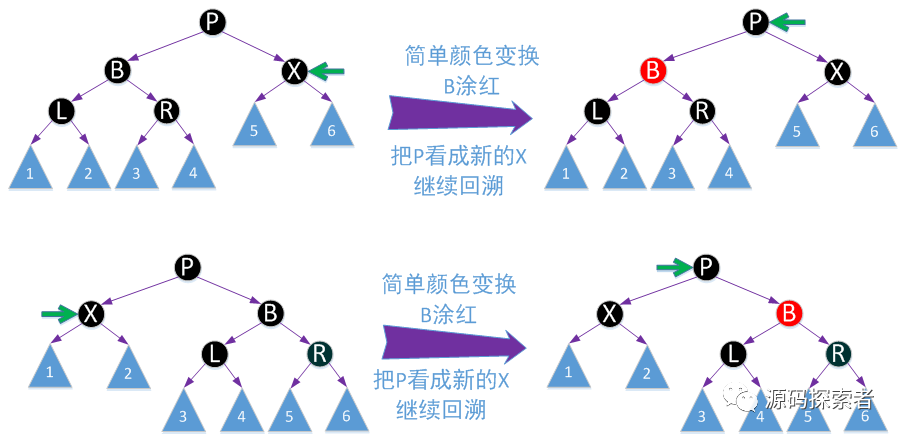
2-3-4树处理:以如下这个为例,其他读者自行推演,只要读懂这个,其他应该是可以自己搞定的
红黑树
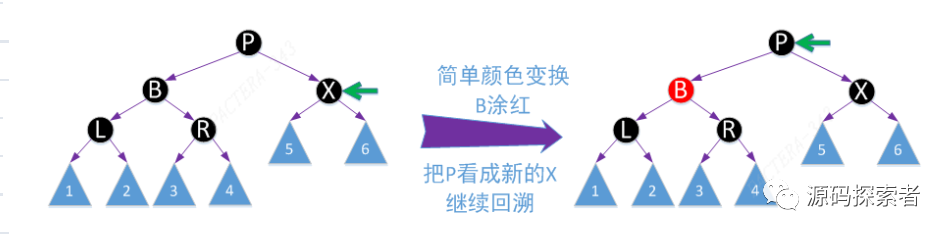
2-3-4树演变过程
对应2-3-4树删除操作中兄弟节点为2节点,父亲节点也为2节点,父节点key下移与兄弟节点合并,已父节点看成新的X,继续回溯。

(4.3.4)红兄(黑侄黑父)
红黑树处理:下面四张图列出了2种不同场景删除节点为了重新保持平衡而进行的调整方法
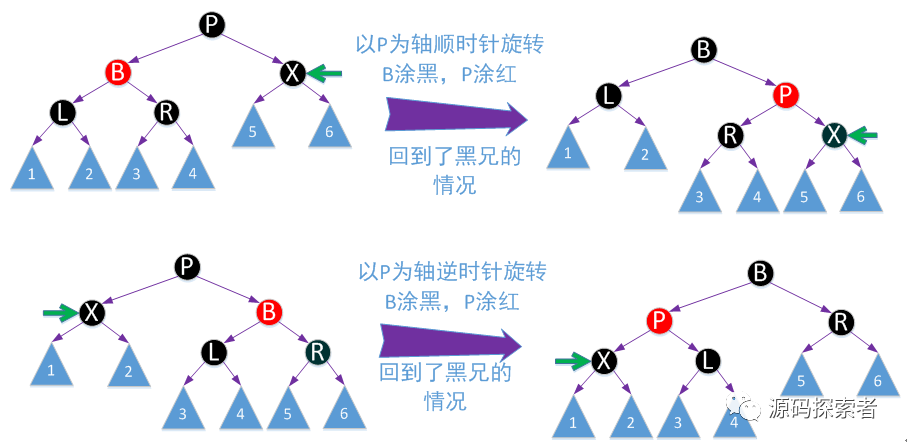
2-3-4树处理:以如下这个为例,其他读者自行推演,只要读懂这个,其他应该是可以自己搞定的
红黑树
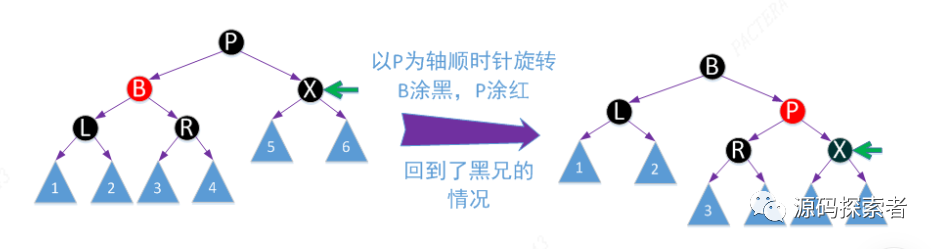
2-3-4树演变过程
经过调整之后,此时我们又回到上面讨论过的了黑兄的情况

这篇关于从2-3-4叉树到红黑树(下)--java集合源码体系研究之基础,让你面试胖揍面试官的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






