本文主要是介绍相机标定:张正友标定原理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文来自公众号“AI大道理”
——————
计算机视觉的源头是相机,因此我们有必要对相机有所了解。
原始相机拍摄的图像一般都会有所畸变,导致画面和实际观测的有所排查,为了让相机拍摄的图像和肉眼观察的一致,就需要进行相机标定,获得相机参数,从而进行校正。
![]()
1、相机模型
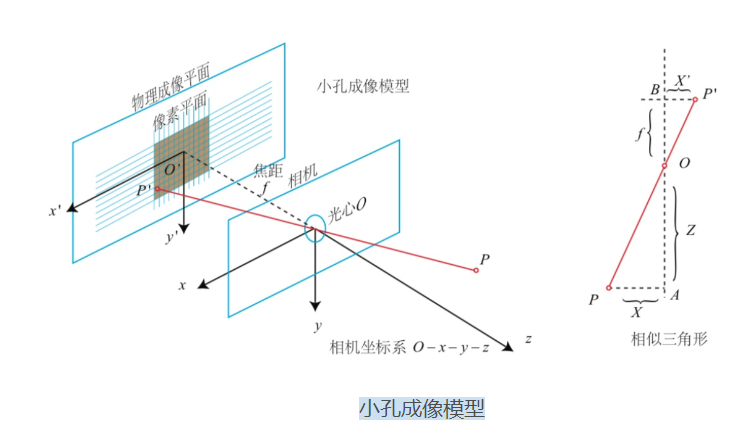
相机是如何成像的?
光束从物体表面反射,经过相机镜头,到达感光原件,这一系列物理过程可以通过数学公式表达,最终变成一个简单的矩阵操作将三维空间中的点对应到图片的一个像素。
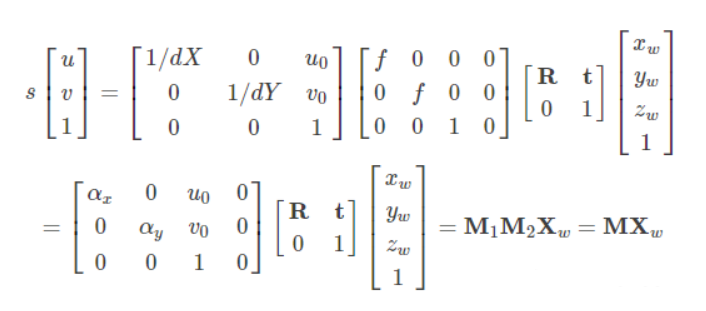
![]()
2、为什么要相机标定?
我们知道实际使用的相机镜头都是透镜,物理上只有通过光心的光线才是沿直线传播的,而大部分的光线在通过透镜后会发生折射,从而在一定程度上改变传播的角度。越靠近透镜的边缘,改变的角度也就越大,这会造成相机所成的像产生距离上的拉伸以及形状的改变,这个现象称为相机畸变。
而标定操作其实就是通过一系列的计算校准后得到修正参数,通过这些参数修正后就可以得到与我们人眼看到的景象相同的图像,也就是将三维景象转换成去除畸变后的二维图像。
进行摄像机标定的目的:求出相机的内、外参数,以及畸变参数。
标定相机后通常是想做两件事:一个通过相机标定可以校正这种镜头畸变矫正畸变,生成矫正后的图像;另一个是根据获得的图像重构三维场景。
![]()
3、相机的畸变
通常分为三大类,径向畸变、离心畸变以及薄棱镜畸变。
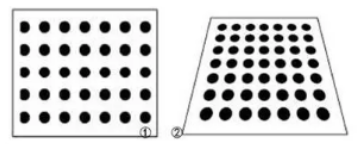
(1)径向畸变
使像点产生径向位置的偏差称为径向畸变。这也是相机中最常见的一种畸变,因为光线通过透镜一定会产生折射。径向畸变又可以具体分为正向枕形畸变、和负向桶形畸变。

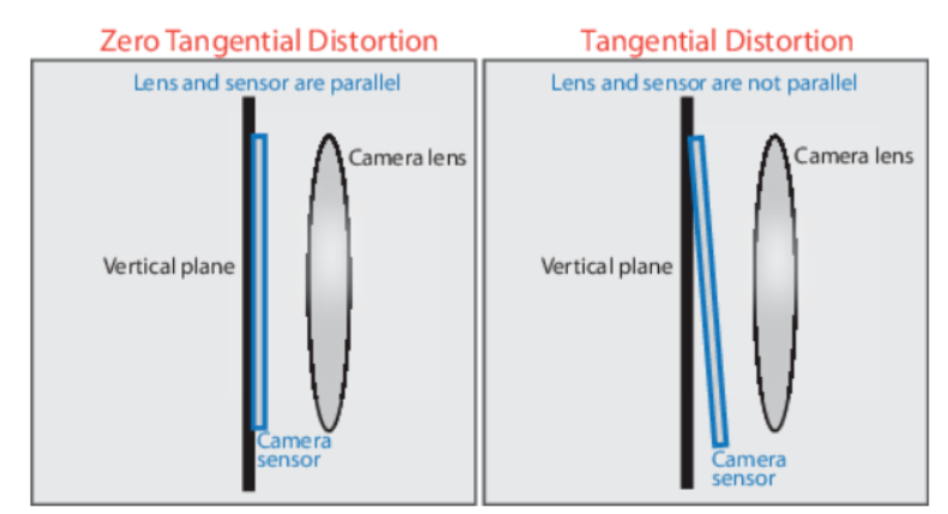
(2)切向畸变
相机的光学中心与几何中心不一致(镜头各器件的光学中心)所造成的畸变称为离心畸变。广义上讲,离心畸变既包含径向畸变,又包含镜头主光轴不对称所造成的切向畸变(不过我们通常将径向畸变单独分成一类)。
(3)薄棱镜畸变
镜头设计缺陷与加工安装误差所造成的畸变称为薄棱镜畸变,这种畸变会同时引起径向畸变和切向畸变(想象一下相机的镜头安装的不正,或者镜头不够平整)。高价位的镜头可以忽略薄棱镜畸变。
![]()
4、标定方法
-
相机自标定法
-
基于主动视觉的标定方法
-
基于标定物的相机标定方法
![]()
5、张正友标定法
张氏标定法属于第三种方法。
张氏标定,简单来说就是个通过单应矩阵的约束求解相机内参的过程。
张氏标定法只关注径向畸变,通过五个左右的畸变系数进行修正,通常为k1,k2,p1,p2,k3。
k的个数通过计算的结果与修正的效果进行调整,可多可少,实际计算过程中,如果考虑太多高阶的畸变参数,会导致标定求解的不稳定。
矩阵A包含5个元素,需要3组H才能解出A的唯一封闭解,因此在标定时需拍摄3组以上的图片。
1)图像点获取
张正友的方法是,拿一个棋盘格图像,通过角点检测,得到角点在图像里的坐标。
2)棋盘的排放
算法是基于2D模型的,如果棋盘摆放的不平整,肯定会造成很大的影像。
3)图像多少
标定原理上至少3张,一般要大于10张。
4)图片的角度
太大的角度对于角点提取的精度影像比较大,所以保持在45度以内比较好。
5)张正友标定的空间坐标系
以标定板左上角第一个角点为原点,水平为x坐标,垂直为y坐标,标定板到相机的距离为z坐标。
![]()
6、相机标定参数
标定模型:
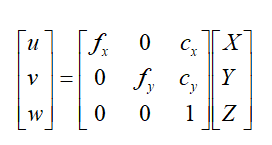
世界坐标->相机坐标->图像坐标->像素坐标:
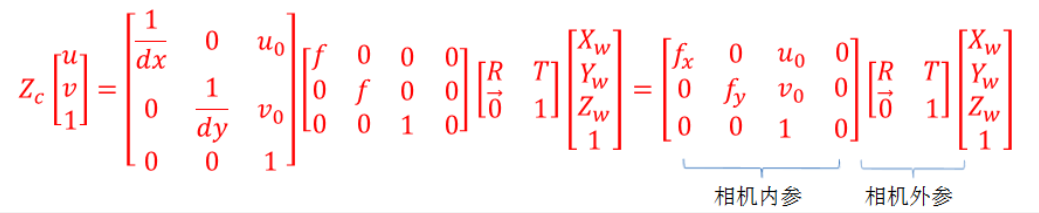
内参:
fx、fy: 单位长度的像素个数
cx、cy: 主点坐标
k1、k2、k3、p1、p2: 畸变系数, 径向三个,切向两个
外参:
R、T: 旋转和平移矩阵
实例:
现以NiKon D700相机为例进行求解其内参数矩阵:
焦距 f=35mm ,最高分辨率:4256×2832 ,传感器尺寸:36.0×23.9mm。
根据以上定义可以有:
u0=4256/2=2128, v0=2832/2=1416, dx=36.0/4256, dy=23.9/2832,
fx = f/dx = 4137.8 , fy = f/dy = 4147.3。
其中相机的内参和外参可以通过张正友标定获取。
![]()
7、相机标定实验
步骤1:固定相机,不同角度移动标定板获取图片,至少三张

步骤2:python相机标定或者matlab相机标定
matlab:
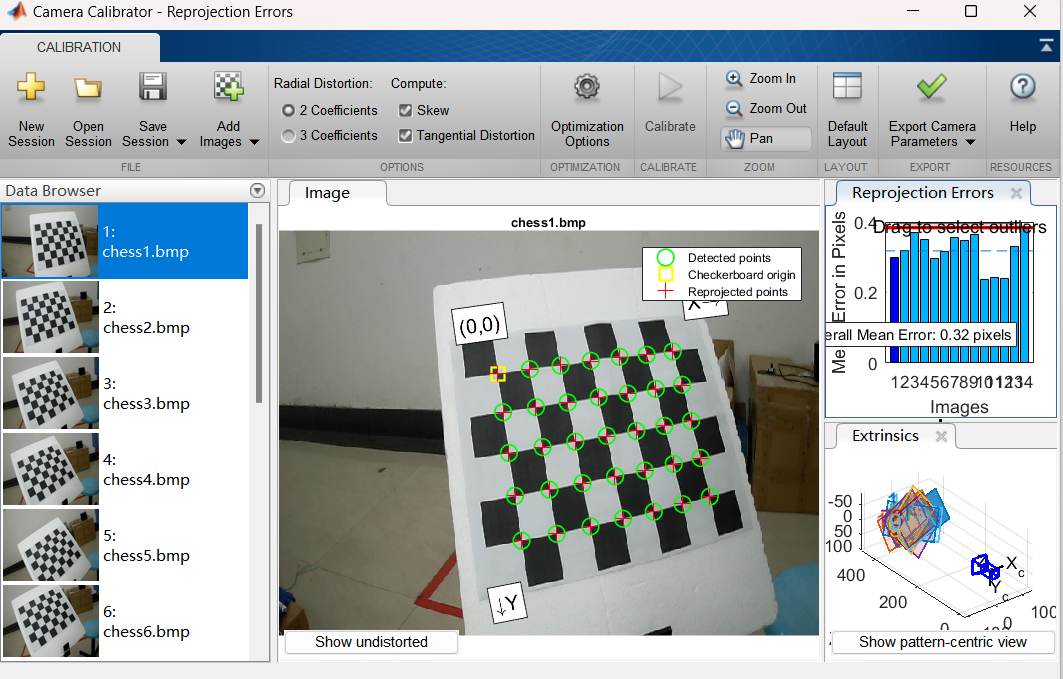

python:
1)特征点检测
获取像素点imgpoints,对棋盘进行角点检测,映射到图片中获取像素点。共35个,因为5*7。

[1,0,0]就是黑白格的坐标,以1为单位。
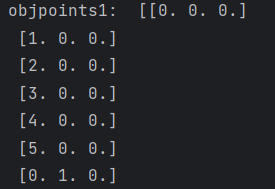
2)获取特征点对应的像素点的坐标
[1417,435]是特征点在图像的坐标。
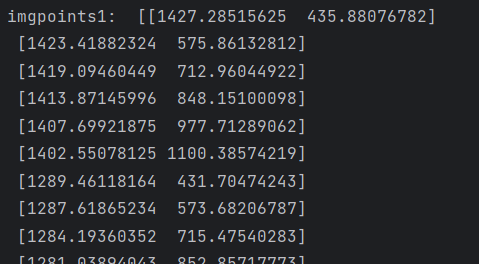
3)空间坐标与像素坐标一一对应的标定
cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
步骤3:旋转向量->旋转矩阵
相机标定得到的R和T如下:
可见并非我们所熟悉的3*3,而是每张图片都有一个对应的R和T,这个并不是我们想要的结果,因为我们想要唯一的一个参数使得可以应对所有情况。
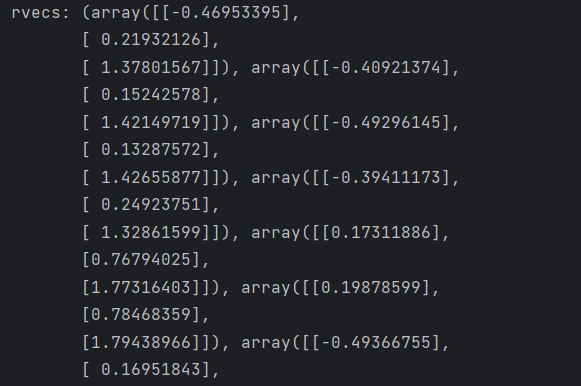
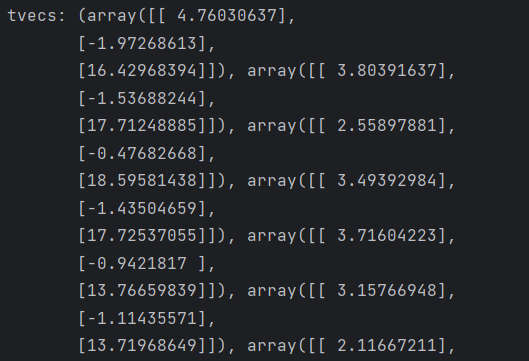
外参还需要单独求解。
外参标定算法及流程:
求解外参是一个PNP(Perspective-N-Point)问题。
如果场景的三维结构已知,利用多个控制点在三维场景中的坐标及其在图像中的透视投影坐标即可求解出摄像机坐标系与表示三维场景结构的世界坐标系之间的绝对位姿关系,包括绝对平移向量T以及旋转矩阵R
对于透视投影来说,要使得PNP问题有确定解,需要至少三组控制点。
# 求解旋转矩阵
retval, rvec, tvec = cv2.solvePnP(objpoints1, imgpoints1, mtx,
dist)
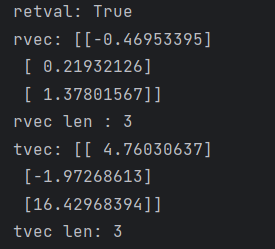
的确得到了唯一的一个参数,但发现这个参数就是上面的第一个图片的参数。
但是还不是3*3的,还需要进行转换。此时旋转参数叫旋转向量,要转为旋转矩阵。
转换方法为罗德里格斯旋转公式。
# 旋转向量和旋转矩阵的互相转换
rotationMatrix, _ = cv2.Rodrigues(rvec)

终于得到了一个适应全部图片的3*3的旋转矩阵,和1*3的平移矩阵。
这两个参数可以将世界坐标和相机坐标进行转换。
(灵魂的拷问:至于为什么就是第一张图片的参数呢?莫非第一张图片就能代表全部了?或者任何一种标定的图片的旋转矩阵就可以当做全局的旋转矩阵?还是说实验过程有问题?)
![]()
8、图像校正
使用上面获得的摄像头矩阵(内参矩阵)和畸变系数 进行畸变矫正。
校正公式:
径向畸变:
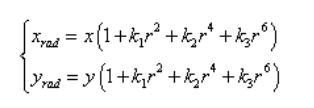
切向畸变:

综合以上两种畸变,得到畸变坐标:
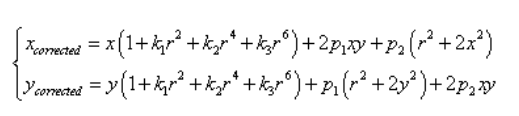
输入图像:

校正方法:
cv2.undistort(gray, mtx, dist, None, mtx)
校正效果:

![]()
9、总结
标定相机后通常是想做两件事:
一个通过相机标定可以校正这种镜头畸变矫正畸变,生成矫正后的图像;
另一个是根据获得的图像重构三维场景。
下来将利用相机内外参进行三维重构,即图像坐标转世界坐标。

——————
浅谈则止,细致入微AI大道理
扫描下方“AI大道理”,选择“关注”公众号
—————————————————————

—————————————————————
投稿吧 | 留言吧
这篇关于相机标定:张正友标定原理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







