Bounded Biharmonic Weigths for Real-Time Deformation

本文主要是介绍Bounded Biharmonic Weigths for Real-Time Deformation，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

3.1 Formulation

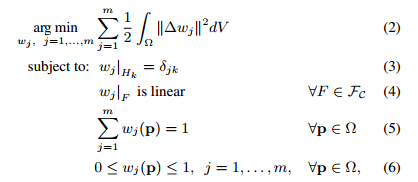
这里写图片描述
{
First of all, let me explain the physical meaning of the objective function.
The function tries to make the weight of each anchor point on each point have least changed. The ideal situation of the objective function is $\Delta \omega_j = 0$ which is in accord with the Laplacian equation.

[refered from [1] at page 5]
}

3.4 Implementation

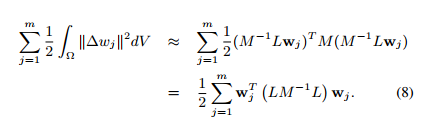
这里写图片描述
{
Here, I wanna derive this formula.

[refered from [1] at page 17]
Here, we let $u_j = \Delta \omega_j$ .

[refered from [2] at formula (9)]
In this paper, it assumes $\Delta u= v.$ As to our case, let $u_j=\omega_j, v_j=\Delta u_j=\Delta \omega_j$ . Therefore, the objective function can be expressed as:

\sum j = 1 m 1 2 \int Ω ∥ Δ ω j ∥ 2 d V = \sum j = 1 m 1 2 \int Ω ∥ v j ∥ 2 d V

$\sum_{j=1}^m \frac{1}{2} \int_{\Omega}\|\Delta \omega_j\|^2dV = \sum_{j=1}^m \frac{1}{2} \int_{\Omega}\|v_j\|^2dV$
According to formula (2.60), it equals to:

\sum j = 1 m 1 2 \int Ω ∥ v j ∥ 2 d V = 1 2 \sum j = 1 m \int Ω ∥ v j ∥ 2 d V = 1 2 \sum j = 1 m v T j M v j

$\sum_{j=1}^m \frac{1}{2} \int_{\Omega}\|v_j\|^2dV=\frac{1}{2}\sum_{j=1}^m \int_{\Omega}\|v_j\|^2dV = \frac{1}{2}\sum_{j=1}^mv_j^TMv_j$
According to the left-bottom equation of (9), we can easily get

vj $v_j$ :

v j = M - 1 L u j = M - 1 L w j

$v_j=M^{-1}Lu_j=M^{-1}Lw_j$
}

Then, I would like to analysis the matlab source code:

% This is a script that demos computing Bounded Biharmonic Weights
% automatically for a 2D shape.
%
% This file and any included files (unless otherwise noted) are copyright Alec
% Jacobson. Email jacobson@inf.ethz.ch if you have questions
%
% Copyright 2011, Alec Jacobson (jacobson@inf.ethz.ch)
%% NOTE: Please contact Alec Jacobson, jacobson@inf.ethz.ch before
% using this code outside of an informal setting, i.e. for comparisons.%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Load a mesh
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% input mesh source: *.obj, *.off, *.poly, or *.png
mesh_source = 'woody.obj';
% should input mesh be upsampled
upsample_mesh = false;if(~isempty(regexp(mesh_source,'\.(off|obj)$')))% load a mesh from an OBJ[V,F] = load_mesh(mesh_source);%顶点存储V中,在2维空间中,V为 #V * 2矩阵%面的索引存储在F中,在2维空间中,F为 #F * 3矩阵% only keep x and y coordinates, since we're working only in 2DV = V(:,1:2);
elseif ~isempty(regexp(mesh_source,'\.poly$'))% load a mesh from a .POLY polygon file format% Triangulate in two-passes. First pass with just angle constraint forces% triangles near the boundary to be small, but internal triangles will be very% graded[V,F] = triangle(mesh_source,'Quality',30);% phony z-coordinateV = [V, zeros(size(V,1),1)];% compute minimum angle min_area = min(doublearea(V,F))/2;% Use minimum area of first pass as maximum area constraint of second pass for% a more uniform triangulation. probably there exists a good heuristic for a% maximum area based on the input edge lengths, but for now this is easy% enough[V,F] = triangle(mesh_source,'Quality',30,'MaxArea',min_area);
elseif ~isempty(regexp(mesh_source,'\.png$'))% load a mesh from a PNG image with transparency[V,F] = png2mesh(mesh_source,1,50);
end% upsample each triangle
if(upsample_mesh)[V,F] = upsample(V,F);
end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Place controls on mesh
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% display mesh
tsurf(F,V)
axis equal;
fprintf( ...['\nCLICK on mesh at each location where you would like to add a ' ...'point handle.\n' ...'Press ENTER when finished.\n\n']);
% User clicks many times on mesh at locations of control points
try[Cx,Cy] = getpts;
catch e% quit early, stop scriptreturn
end
% store control points in single #P by 2 list of points
C = [Cx,Cy];%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Bind controls to mesh
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Note: This computes the "normalized" or "optimized" version of BBW, *not* the
% full solution which solve for all weights simultaneously and enforce
% partition of unity as a proper contstraint. % Compute boundary conditions
[b,bc] = boundary_conditions(V,F,C);
% Compute weights
if(exist('mosekopt','file'))% if mosek is installed this is the fastest optionW = biharmonic_bounded(V,F,b,bc,'conic');
else% else this uses the default matlab quadratic programming solverW = biharmonic_bounded(V,F,b,bc,'quad',true);
end
% Normalize weights
W = W./repmat(sum(W,2),1,size(W,2));%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Deform mesh via controls
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Display mesh and control points and allow user to interactively deform mesh
% and view weight visualizations% Commented out are examples of how to call "simple_deform.m" with various options
simple_deform(V,F,C,W,'ShowWeightVisualization');
% interactively deform point controls
%simple_deform(V,F,C,W)

After that we analysis the boundary_conditions.m source code

function [b,bc] = boundary_conditions(V,F,C,P,E,CE)% BOUNDARY_CONDITIONS% Compute boundary and boundary conditions for solving for correspondences% weights over a set of mesh (V,F) with control points C(p,:) and control% bones C(E(:,1),:) --> C(E(:,2),:)%% [b,bc] = boundary_conditions(V,F,C,P,E,CE)%% % same as [b,bc] = boundary_conditions(V,F,C,1:size(C,1),[])% [b,bc] = boundary_conditions(V,F,C) %% Inputs:%  V  list of vertex positions%  F  list of face indices (not being used...)%  C  list of control vertex positions %  P  list of indices into C for point controls, { 1:size(C,1) }%  E  list of bones, pairs of indices into C, connecting control vertices, %    { [] }%  CE  list of "cage edges", pairs of indices into ***P***, connecting%    control ***points***. A "cage edge" just tells point boundary conditions %    to vary linearly along straight lines between the end points, and to be%    zero for all other handles. { [] }% Outputs% boundary_conditions.m
%%%%%%%% Added by seamanj %%%%%%%%%%%%%%
% b为边界点的索引
% bc 为矩阵，每行代表某一边界点（具体是哪一边界点由b来索引确定），每列代表某一控制            
% 点，矩阵内容代表某一控制点对某一边界点的影响权值。所有控制点对一边界点的影响权
% 值之和应该为1，所以每行按列相加也应该为1,当然所有控制点对任意顶点的影响权值之和      
% 应该为1,这里的边界点属于特殊的顶点 
%
% 注意,这里我想解释下边界点的含义,边界点其实是顶点的一种,这里用户用鼠标按下的点
% 为控制点,那么离控制点最近的点变成了我们的边界点,因为边界点必须为mesh上的顶点
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%  b  list of boundary vertices%  bc list of boundary conditions, size(boundary) by # handles matrix of%    boundary conditions where bc(:,i) are the boundary conditions for the %    ith handle ( handle order is point handles then edges handles: P,E)% % Copyright 2011, Alec Jacobson (jacobson@inf.ethz.ch)%% See also: biharmonic_bounded %% control vertices and domain should live in same dimensionsassert(size(C,2) == size(V,2));% number o dimensionsdim = size(C,2);% set point handle indices and arrange to be column vectorif(exist('P','var'))if(size(P,1) == 1)P = P';endelse% if point handles weren't given then treat all control vertices as point% handlesP = (1:size(C,1))';end% set default edge list to []if(~exist('E','var'))E = [];end% set default cage edge list to []if(~exist('CE','var'))CE = [];end% P should be either empty or a column vectorassert(isempty(P) || (size(P,2) == 1));% E should be empty or be #bones by 2 list of indicesassert( isempty(E) || (size(E,2) == 2));% number of point controlsnp = numel(P);% number of bone controlsne = size(E,1);% number of control handlesm = np + ne;% number of mesh verticesn = size(V, 1);% number of control verticesc = size(C,1);% compute distance from every vertex in the mesh to every control vertexD = permute(sum((repmat(V,[1,1,c]) - ...permute(repmat(C,[1,1,n]),[3,2,1])).^2,2),[1,3,2]);% 这里我想稍微解释下,假设V为n*2,那么repmat(V,[1,1,c])则为n*2*c的三维数组,% 其物理意义为:前两维n*2包含了n个顶点,然后把他复制成了C份% 那么repmat(C,[1,1,n])则为c*2*n,其物理意义为:c*2包含了c个控制点,然后复制成% n份,然后呢permute将其第1维和第3维置换了一下,由于第3维表示复制,现在置换过后% 第1维表示复制, permute(repmat(C,[1,1,n]),[3,2,1])则为n*2*c,现在前两维% 表示一个control point,纵向复制n份,然后控制点随着第三维变化,相减后算他们的% 平方,相当于每个控制点与各个顶点的距离平方,注意这里sum(*,2)是按水平方向叠加,%这里计算过后的维数为n*1*c,最后再进行转置,变成n*c*1,这样就变成了每个顶点到控制%点的距离的平方
% vrepmat
% Replicate and tile array%%%%%%%% Added by seamanj %%%%%%%%%%%%%%
% now D is a n*c*1 matrix
%             控制点
%              －－
%      顶点|  每个点到控制点的距离平方
%          |
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% use distances to determine closest mesh vertex to each control vertex% Cv(i) is closest vertex in V to ith control vertex in C[minD,Cv] = min(D);
%%%%%%%% Added by seamanj %%%%%%%%%%%%%%
% minD 为每列最小的元素
% Cv中是指哪一个顶点到该控制点距离最小,存储的是该顶点的索引
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% if number of unique closest mesh vertices is less than total number, then% we have contradictory boundary conditionsif(~all(size(unique(Cv)) == size(Cv)))warning('Multiple control vertices snapped to the same domain vertex');end% boundary conditions for all vertices NaN means no boundary conditionsbc = repmat(NaN,[n m]);%%%%%%%% Added by seamanj %%%%%%%%%%%%%%
% 让在控制点的权值为1
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% compute boundary conditions for point handlesif( ~isempty(P) )bc(Cv(P),:) = eye(np,m);% 这里先用P当索引去引用Cv,找到边界点的索引,然后用边界点的索引去引用对应的行  end%%%%%%%% Added by seamanj %%%%%%%%%%%%%%
% 让在骨骼上的点权值为1
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Compute boundary conditions for bone edge handlesif(~isempty(E))% average edges length to give an idea of "is on edge" toleranceh = avgedge(V,F);% loop over bonesfor( ii = 1:size(E,1) )[t,sqr_d] = project_to_lines(V,V(Cv(E(ii,1)),:),V(Cv(E(ii,2)),:));on_edge = ((abs(sqr_d) < h*1e-6) & ((t > -1e-10) & (t < (1+1e-10))));% get rid of any NaNs on these rows% WARNING: any (erroneous) point handle boundary conditions will get% "normalized" with bone boundary conditionsold = bc(on_edge,:);old(isnan(old)) = 0;bc(on_edge,:) = old;%seamanj:这里逐渐将NaN变为0,这样就不会重复变0了,没太大的实际意义%bc(on_edge,:) = isnan(bc(on_edge,:)).*0 + ~isnan(bc(on_edge,:)).*bc(on_edge,:);bc(on_edge,np+ii) = 1;%seamanj:行序表示在骨骼上的顶点序号,列序先Pass掉np,即上面控制点的个数,后面是骨骼的序号endend
%%%%%%%% Added by seamanj %%%%%%%%%%%%%%
% 让在边界上的点的权值线性变化
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% compute boundary conditions due to cage edgesif(~isempty(CE))% loop over cage edgesfor( ii = 1:size(CE,1) )[t,sqr_d] = project_to_lines(V,V(Cv(P(CE(ii,1))),:),V(Cv(P(CE(ii,2))),:));h = avgedge(V,F);on_edge = ((abs(sqr_d) < h*1e-6) & ((t > -1e-10) & (t < (1+1e-10))));% get rid of any NaNs on these rows% WARNING: clobbers any (erroneous) point handle boundary conditions on% points that are on bones)old = bc(on_edge,:);old(isnan(old)) = 0;bc(on_edge,:) = old;bc(on_edge,CE(ii,1)) = 1 - t(on_edge);bc(on_edge,CE(ii,2)) = t(on_edge);%注意如果该点在边界上,那么转换成边界两端点对该点的权值,Cv(P(CE(ii,2))%CE代表边端点在handle里面的索引,然后用该索引去索引handle点endendindices = 1:n;% boundary is only those vertices corresponding to rows with at least one non% NaN entryb = indices(any(~isnan(bc),2));bc = bc(b,:);% replace NaNs with zerosbc(isnan(bc)) = 0;
%%%%%%%% Added by seamanj %%%%%%%%%%%%%%
% 归一化处理  满足所有控制点对点p的权值和为1
% A = 1     2
%     3     4
% sum(m,2) =  对每行按列求和
% 3
% 7
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%  bc(any(bc,2),:)  = bc(any(bc,2),:) ./ repmat(sum(bc(any(bc,2),:),2),1,size(bc,2));
end

Then we get into solving the weights.

function W = biharmonic_bounded(V,F,b,bc,type,pou,low,up)% BIHARMONIC_BOUNDED Compute biharmonic bounded coordinates, using quadratic% optimizer%% W = biharmonic_bounded(V,F,b,bc,type,pou)% W = biharmonic_bounded(V,F,b,bc,type,pou,low,up)%% Inputs:%  V  list of vertex positions%  F  list of face indices, for 3D F is #F by 4, for 2D F is #F by 3%seamanj added: for 3D it's tetrahedron, for 2D it's triangle%%  b  list of boundary vertices%  bc list of boundary conditions, size(boundary) by # handles matrix of%    boundary conditions where bc(:,i) are the boundary conditions for the %    ith handle% 这里只处理了控制点的情况,骨骼和cage没有在此处理%  Optional:%    type  type of optimizer to use {best available}:%      'quad'%      'least-squares'%      'conic'%    pou  true or false, enforce partition of unity explicitly {false}%    low  lower bound {0}%    up  upper bound {1}%  %% Outputs:%  W  weights, # vertices by # handles matrix of weights%% Copyright 2011, Alec Jacobson (jacobson@inf.ethz.ch)%% See also: boundary_conditions%% set default for enforcing partition of unity constraintif ~exist('pou','var') || isempty(pou)pou = false;end% number of verticesn = size(V,1);% number of handlesm = size(bc,2);% Build discrete laplacian and mass matrices used by all handles' solvesif(size(F,2)==4)fprintf('Solving over volume...\n');L = cotmatrix3(V,F);M = massmatrix3(V,F,'barycentric');elseL = cotmatrix(V,F);M = massmatrix(V,F,'voronoi');end% default boundsif ~exist('low','var') || isempty(low)low = 0;endif ~exist('up','var') || isempty(up)up = 1;end% set default optimization methodif ~exist('type','var') || isempty(type)if(exist('mosekopt'))% if mosek is available then conic is fastesttype = 'conic';else% if we only have matlab then quadratic is defaulttype = 'quad';endend%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% SET UP SOLVER%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% check for mosek and set its parametersparam = [];% Tolerance parameter% >1e0 NONSOLUTION% 1e-1 artifacts in deformation% 1e-3 artifacts in isolines% 1e-4 seems safe for good looking deformations% 1e-8 MOSEK DEFAULT SOLUTION% 1e-14 smallest allowed valueif(exist('mosekopt','file'))if(strcmp(type,'quad') || strcmp(type,'least-squares'))param.MSK_DPAR_INTPNT_TOL_REL_GAP = 1e-10;elseif(strcmp(type,'conic'))param.MSK_DPAR_INTPNT_CO_TOL_REL_GAP = 1e-10;endmosek_exists = true;else mosek_exists = false;if(verLessThan('matlab','7.12'))% old matlab does not solve quadprog with sparse matrices: SLOW% solution: dowloand MOSEK or upgrade to 2011a or greaterwarning([ ...'You are using an old version of MATLAB that does not support ' ...'solving large, sparse quadratic programming problems. The ' ...'optimization will be VERY SLOW and the results will be ' ...'INACCURATE. Please install Mosek or upgrade to MATLAB version >= ' ...'2011a.']);else% Tell matlab to use interior point solver, and set tolerance% 1e-8 MATLAB DEFAULT SOLUTION (very low accuracy)% 1e-10 (low accuracy)% 1e-12 (medium-low accuracy)% 1e-14 (medium accuracy)% 1e-16 (high accuracy)param = optimset( ...'TolFun',1e-16, ...'Algorithm','interior-point-convex', ...... % 'Algorithm','active-set', ...'MaxIter', 1000, ...'Display','off');endend%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% SET UP PROBLEM AND SOLVE%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%if(pou)% Enforce partition of unity as explicity constraints: solve for weights% of all handles simultaneously% seamanj: Enforce partition of unity 这里的归一性,代表所有控制点对某顶点的权值和应该为1if(strcmp(type,'quad'))% biharmonic system matrixQi = L*(M\L);% x = A\B % divides the Galois array A into B to produce a particular solution % of the linear equation A*x = B. In the special case when A is a % nonsingular square matrix, x is the unique solution, inv(A)*B, % to the equation.Q = sparse(m*n,m*n);% Q is sparse matrix with Qi along diagonalfor ii = 1:md = (ii - 1)*n + 1;Q(d:(d + n-1), d:(d + n-1)) = Qi;end% linear constraints: partition of unity constraints and boundary% conditionsPA = repmat(speye(n,n),1,m);Pb = ones(n,1);%      1             2                          m%----------------------------------------------------% 1             1                           1%   1             1                           1%     ...           ...           ...           ...%         1             1                           1%            1             1                           1%然后未知量为:%  w_11%  w_21%  ...%  w_n1%  w_12%  w_22%  ...%  w_n2%  ...%  w_1m%  w_2m%  ...%  w_nm%其中w_ij表示第j个控制点对第i个顶点的权值%与上面矩阵相乘则得到:w_11 + w_12 + ... + w_1m,则表示所有控制点对某一顶点的权值和应该为1% boundary conditionsBCAi = speye(n,n);BCAi = BCAi(b,:);%b为控制点的序号,这里把控制点的行选出,这里行代表控制点,列代表顶点BCA = sparse(m*size(BCAi,1),m*size(BCAi,2));% BCA is sparse matrix with BCAi along diagonalfor ii = 1:mdi = (ii - 1)*size(BCAi,1) + 1;dj = (ii - 1)*size(BCAi,2) + 1;BCA(di:(di + size(BCAi,1)-1), dj:(dj + size(BCAi,2)-1)) = BCAi;end% 然后BCA将BCAi从行列扩展m倍,然后对角线矩阵为BCAi,相当于BCAi沿对角线的方向% 扩展了m倍BCb = bc(:);%每列往上一列下面叠加,形成一个列向量%BCA*x=BCb,x解出来的值为(n*m,1)的列向量,其中数据以列叠加在一起,每列表示%某一控制点对所以顶点的权值的分布%seamanj:
%     A = [1 2; 3 4];
%     A(:)
%     ans =
%          1
%          3
%          2
%          4% set boundsux = up.*ones(m*n,1);lx = low.*ones(m*n,1);if(mosek_exists)fprintf('Quadratic optimization using mosek...\n');elsefprintf('Quadratic optimization using matlab...\n');endfprintf( [ ...'  minimize:     x''LM\\Lx\n' ...'subject to: %g <= x <= %g, ∑_i xi = 1\n'], ...low,up);tic;W = quadprog(Q,zeros(n*m,1),[],[],[PA;BCA],[Pb;BCb],lx,ux,[],param);%x解出来的值为(n*m,1)的列向量,其中数据以列叠加在一起,每列表示%某一控制点对所以顶点的权值的分布tocW = reshape(W,n,m);
%     seamanj:      
%     A = [1:12];
%     reshape(A,3,4)
% 
%     ans =
% 
%     1     4     7    10
%     2     5     8    11
%     3     6     9    12elseerror( [ ...'Enforcing partition of unity only support in conjunction with ' ...'type=''quad''']);end%后面的情况差不多,我就不一一分析了,只不过用了其他的优化方式else % Drop partition of unity constraints, solve for weights of each handle% independently then normalize to enforce partition of unity% seamanj:这里没有将归一性作为constrain,而是最后去单位化if(strcmp(type,'quad'))% build quadratic coefficient matrix (bilaplacian operator)Q = L*(M\L);% set boundsux = up.*ones(n,1);lx = low.*ones(n,1);elseif(strcmp(type,'least-squares'))% solve same problem but as least-squares problem see mosek documention% for detailsI = speye(n);Z = sparse(n,n);Q = [Z,Z;Z,I];F = sqrt(M)\L;c = zeros(n,1);B = [F,-I];ux = [up.*ones(n,1) ;  Inf*ones(n,1)];lx = [low.*ones(n,1); -Inf*ones(n,1)];elseif(strcmp(type,'conic'))% solve same problem but as conic problem see mosek documention for% detailsF = sqrt(M)\L;prob.c = [zeros(2*n,1); 1];I = speye(n);prob.a = [F,-I,zeros(n,1)];prob.blc = zeros(n,1);prob.buc = zeros(n,1);prob.bux = [ up.*ones(n,1);  Inf*ones(n,1);  Inf];prob.blx = [ low.*ones(n,1); -Inf*ones(n,1); -Inf];prob.cones = cell(1,1);prob.cones{1}.type = 'MSK_CT_QUAD';t_index = 2*n +1;z_indices = (n+1):(2*n);prob.cones{1}.sub = [t_index z_indices];elseerror('Bad type');end% number of handlesm = size(bc,2);% allocate space for weightsW = zeros(n,m);tic;% loop over handlesfor i = 1:mif(strcmp(type,'quad'))% enforce boundary conditions via lower and upper bounds%lx(b) = bc(:,i);%ux(b) = bc(:,i);Aeq = speye(n,n);Aeq = Aeq(b,:);if(mosek_exists)fprintf('Quadratic optimization using mosek...\n');else  fprintf('Quadratic optimization using matlab...\n');endfprintf( [ ...'  minimize:     x''LM\\Lx\n' ...'subject to: %g <= x <= %g\n' ], ...low,up);% if mosek is not available, then matlab will complain that sparse% matrices are not yet supported...[x,fval,err] = quadprog(Q,zeros(n,1),[],[],Aeq,bc(:,i),lx,ux,[],param);if(err ~= 1)fprintf([...'----------------------------------------------------------\n' ...'ERROR ('  num2str(err) ',' num2str(fval) '):' ...' solution may be inaccurate...\n' ...'----------------------------------------------------------\n' ...]);endelseif(strcmp(type,'least-squares'))% enforce boundary conditions via lower and upper boundslx(b) = bc(:,i);ux(b) = bc(:,i);fprintf('Quadratic optimization using mosek...\n');fprintf([ ...'  minimize:       z''z\n' ...'  subject to: sqrt(M)\\Lx - z = 0\n' ...'  and          %g <= x <= %g\n'] , ...low,up);x = quadprog(Q,zeros(2*n,1),[],[],B,c,lx,ux,[],param);elseif(strcmp(type,'conic'))prob.bux(b) = bc(:,i);prob.blx(b) = bc(:,i);fprintf('Conic optimization using mosek...\n');fprintf([ ...'  minimize:         t\n' ...'  subject to: sqrt(M)\\Lx - z = 0,\n' ...'             t >= sqrt(z''z),\n' ...'               %f <= x <= %f\n'], ...low,up);[r,res]=mosekopt('minimize echo(0)',prob,param);% check for mosek errorif(r == 4006)warning(['MOSEK ERROR. rcode: ' ...num2str(res.rcode) ' ' ...res.rcodestr ' ' ...res.rmsg ...'The solution is probably OK, but ' ...'to make this error go away, increase: ' ...'MSK_DPAR_INTPNT_CO_TOL_REL_GAP' ...n]);elseif(r ~= 0)error(['FATAL MOSEK ERROR. rcode: ' ...num2str(res.rcode) ' ' ...res.rcodestr ' ' ...res.rmsg]);end% extract solution from resultx = res.sol.itr.xx;end% set weights to solution in weight matrixW(:,i) = x(1:n);fprintf('Lap time: %gs\n',toc);endt = toc;fprintf('Total elapsed time: %gs\n',t);fprintf('Average time per handle: %gs\n',t/m);end
end